Параллелепипед - это геометрическое тело, у которого все стороны являются параллельными и соответственно равными парами. Он имеет шесть граней, включая две параллельные основания и четыре боковые стороны. Если секция треугольника необходима в параллелепипеде, то это означает, что необходимо найти плоскость, проходящую через пару ребер параллелепипеда и образующую треугольник с одной из его граней.
Для нахождения и вычисления секции треугольника внутри параллелепипеда, необходимо рассмотреть его грани и корректно определить соответствующие ребра и углы. Затем можно использовать различные математические методы и формулы, такие как теорема Пифагора или теорема косинусов, чтобы рассчитать необходимые стороны и углы треугольника.
Важно: перед вычислениями необходимо убедиться, что все измерения и значения достоверны и правильно представлены в соответствующих единицах измерения. Также следует учитывать особенности конкретного параллелепипеда, такие как его форма и размерности, чтобы точно определить, какая часть треугольника будет являться его секцией.
В чем заключается задача?

Задача заключается в нахождении и вычислении секции треугольника, который находится внутри параллелепипеда.
Секция треугольника - это плоский фигурный сегмент треугольника, который находится внутри трех плоскостей параллелепипеда.
Для решения задачи необходимо определить координаты вершин треугольника и затем использовать геометрические формулы и алгоритмы для вычисления площади и других характеристик секции треугольника.
Такая задача может иметь практическое применение в различных областях, например, в инженерии, архитектуре или компьютерной графике.
Почему это важно?

Понимание метода нахождения и вычисления секции треугольника в параллелепипеде имеет множество практических применений. Это позволяет решать задачи в различных областях, включая геометрию, строительство, инженерию и дизайн.
Определение секции треугольника в параллелепипеде является важным шагом при проектировании и изучении трехмерных моделей. Это позволяет точно расположить треугольник в пространстве и определить его размеры и положение относительно других элементов конструкции.
Наличие знаний о секции треугольника в параллелепипеде также полезно при решении задач, связанных с вычислением площади поверхности или объема фигуры. Зная площадь секции треугольника и его высоту, можно легко найти площадь всего треугольника и объем параллелепипеда.
Кроме того, знание метода нахождения и вычисления секции треугольника в параллелепипеде может быть полезно в решении практических задач, связанных с планированием и построением. Например, при размещении окон или дверей в стенах параллелепипедного помещения необходимо точно определить их положение и размеры относительно стен.
Таким образом, понимание и применение метода нахождения и вычисления секции треугольника в параллелепипеде имеет важное практическое значение в различных областях, где требуется работа с трехмерными объектами и конструкциями.
| Номер пункта | Текст пункта |
| 1 | Геометрия |
| 2 | Строительство |
| 3 | Инженерия |
| 4 | Дизайн |
Секция треугольника:
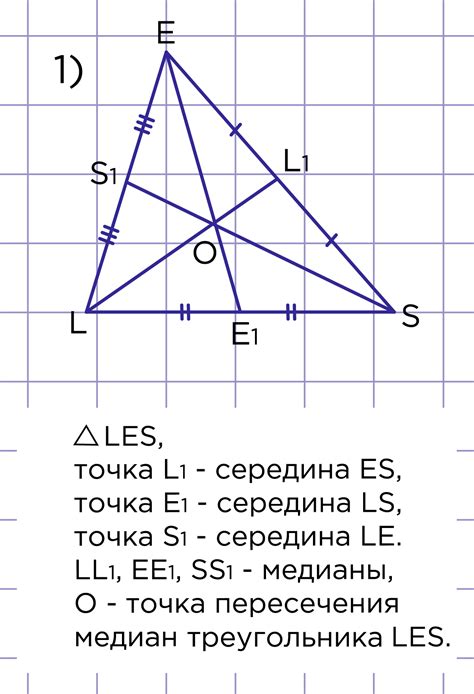
Для нахождения секции треугольника необходимо определить точку, через которую она будет проходить. Эта точка может быть задана координатами или зависеть от других параметров треугольника и параллелепипеда.
После определения точки, можно построить плоскость, проходящую через эту точку и параллельную другой стороне треугольника. Для этого можно использовать методы плоской геометрии, например, задание плоскости через векторное произведение или используя уравнение плоскости.
После построения плоскости, можно определить точки пересечения этой плоскости с сторонами треугольника. Эти точки будут вершинами секции треугольника. Зная координаты вершин, можно вычислить длины сторон и углы секции треугольника.
Вычисление секции треугольника в параллелепипеде может быть полезным при решении различных геометрических задач, например, при определении объема параллелепипеда, содержащего треугольник, или при нахождении площади секции треугольника.
Определение секции треугольника
Для определения секции треугольника в параллелепипеде, необходимо найти точки пересечения прямых сторон треугольника с ребрами параллелепипеда, которые параллельны этим сторонам. Затем, эти точки легко соединить друг с другом и с вершинами треугольника, образуя требуемую секцию.
Важно учитывать, что секция треугольника может быть как плоской, так и выпуклой, в зависимости от взаимного расположения треугольника и параллелепипеда. Для расчета ее площади и длины сторон, можно использовать соответствующие геометрические формулы.
Как найти секцию треугольника в параллелепипеде
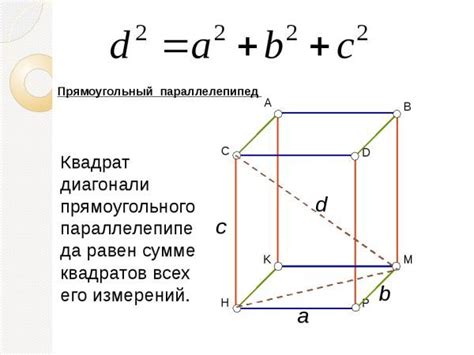
Для нахождения секции треугольника в параллелепипеде необходимо знать координаты вершин треугольника и уравнение плоскости, проходящей через треугольник. Уравнение плоскости может быть найдено с помощью методов аналитической геометрии, таких как нахождение нормали к плоскости и нахождение коэффициентов уравнения плоскости.
После нахождения уравнения плоскости, проходящей через треугольник, можно найти точки пересечения этой плоскости с рёбрами параллелепипеда. Эти точки будут вершинами секции треугольника. Для нахождения координат вершин секции треугольника можно воспользоваться уравнениями прямых, содержащих рёбра параллелепипеда и плоскости, проходящей через треугольник.
После нахождения вершин секции треугольника в параллелепипеде можно построить и визуализировать эту фигуру. Для этого можно воспользоваться графическими инструментами, такими как компьютерная графика или программы моделирования, которые позволяют создавать и изменять геометрические фигуры в трехмерном пространстве.
Как вычислить секцию треугольника:
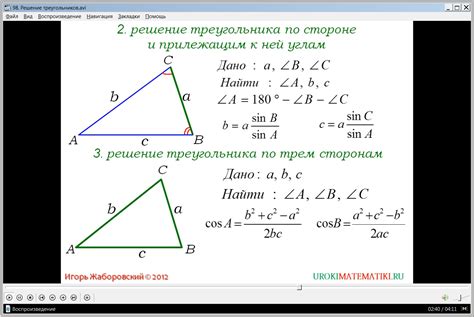
Для вычисления секции треугольника, следуйте следующим шагам:
- Найдите плоскость, содержащую треугольник, с помощью его вершин.
- Найдите точку пересечения этой плоскости с плоскостью параллелепипеда, в котором находится треугольник.
- Прокладывайте прямую линию от этой точки до самого треугольника.
Используя эти шаги, вы сможете вычислить секцию треугольника в параллелепипеде и определить точку, в которой она пересекается с треугольником.
Определение секции треугольника в параллелепипеде
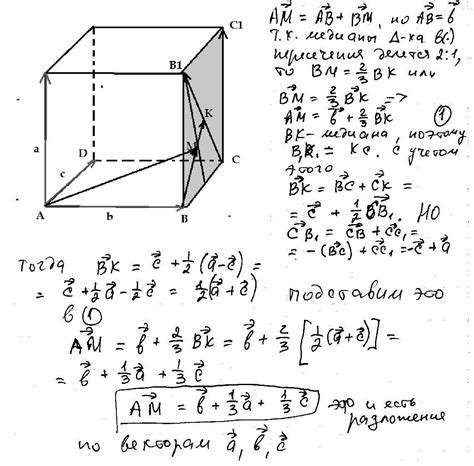
Для определения секции треугольника в параллелепипеде необходимо выполнить следующие шаги:
- Определить плоскость, содержащую треугольник. Для этого можно использовать методы геометрической алгебры, например, вычислить уравнение плоскости по трём точкам треугольника.
- Найти точки пересечения плоскости треугольника с гранями параллелепипеда. Это можно сделать путем решения системы уравнений, состоящей из уравнений плоскости и уравнений граней.
- Проверить, являются ли найденные точки пересечения вершинами треугольника. Для этого необходимо проверить, лежат ли найденные точки пересечения на сторонах треугольника.
- Если все найденные точки пересечения являются вершинами треугольника, то секция треугольника в параллелепипеде полностью совпадает с треугольником. В противном случае, секция будет состоять из вершин треугольника и точек пересечения на его сторонах.
Таким образом, определение секции треугольника в параллелепипеде требует вычисления плоскости, нахождения точек пересечения и проверки их принадлежности треугольнику.
Методы вычисления секции треугольника
Для вычисления секции треугольника в параллелепипеде существуют несколько методов:
- Метод определения площади треугольника по формуле Герона;
- Метод определения площади треугольника по формуле полупериметра;
- Метод определения площади треугольника с использованием векторного произведения;
- Метод определения площади треугольника с использованием координат вершин.
Каждый из этих методов имеет свои особенности и может быть использован в зависимости от конкретной ситуации. Например, метод Герона подходит для вычисления площади треугольника, если известны длины его сторон. Метод полупериметра удобен, когда известны длины сторон и нужно вычислить площадь треугольника в параллелепипеде. Метод векторного произведения позволяет вычислить площадь треугольника, если известны координаты его вершин. Метод с использованием координат вершин применяется, когда требуется вычислить площадь треугольника на плоскости, заданной его вершинами.