Равнодействующая сила – это векторная величина, которая представляет собой результат суммирования всех действующих на тело сил. Знание модуля равнодействующих сил позволяет определить, как будет двигаться тело в соответствии с принципами динамики.
Чтобы найти модуль равнодействующих сил на тело, необходимо знать значения всех сил, действующих на него. Эти силы могут быть как в горизонтальном, так и в вертикальном направлениях. Для нахождения модуля равнодействующей силы необходимо воспользоваться теоремой Пифагора, которая связывает модуль вектора с его проекциями на оси координат.
Примером рассмотрения модуля равнодействующей силы может служить ситуация, когда на тело действуют две силы с модулями 5 Н и 12 Н и они направлены под углом 60° друг к другу. Для вычисления равнодействующей силы можно воспользоваться формулой:
R = sqrt(F1^2 + F2^2 + 2*F1*F2*cosθ)
где R – модуль равнодействующей силы, F1 и F2 – модули исходных сил, θ – угол между этими силами.
Используя данную формулу и подставляя известные данные, можно легко найти модуль равнодействующей силы на тело и определить, как оно будет двигаться под действием этих сил.
Определение модуля равнодействующих сил

Чтобы определить модуль равнодействующих сил на тело, необходимо учесть все силы, действующие на него. В случае, если силы действуют в одной плоскости и направлены вдоль одной оси, их модули просто суммируются. Например, если на тело действуют силы с модулями 10 Н и 5 Н, модуль равнодействующих сил будет равен 15 Н.
Однако, если силы действуют в разных направлениях или не вдоль одной оси, их модули должны быть разложены на составляющие, которые в дальнейшем также суммируются. Для этого можно использовать метод графического или аналитического разложения сил.
Таким образом, понимание и умение определять модуль равнодействующих сил на тело является необходимым для решения многих физических задач и позволяет получить более полное представление о действии сил на тело.
Способы нахождения модуля равнодействующих сил

Модуль равнодействующих сил на тело может быть определен различными способами. Вот несколько из них:
1. Геометрический метод
Геометрический метод основан на использовании векторной суммы сил. Для нахождения модуля равнодействующих сил необходимо векторы сил, действующих на тело, разложить на компоненты и сложить их. Затем найденные компоненты складываются с помощью пифагоровой теоремы и получаем модуль равнодействующих сил.
2. Аналитический метод
Аналитический метод основан на использовании формул и уравнений для определения модуля равнодействующих сил. Он предполагает запись каждой силы как вектора с определенными координатами и последующее сложение этих векторов. Используется система координат для определения положения и направления векторов.
3. Метод треугольника
Метод треугольника - простой и наглядный способ нахождения модуля равнодействующих сил. Он основан на построении треугольника, где каждый вектор силы является стороной треугольника. Модуль равнодействующих сил определяется как гипотенуза этого треугольника.
4. Графический метод
Графический метод включает построение графика векторов сил на графической плоскости. Затем модуль равнодействующих сил определяется как длина вектора-суммы сил на графике. Данный метод позволяет наглядно представить действие всех сил на тело и определить модуль равнодействующих сил.
Выбор и использование способа нахождения модуля равнодействующих сил зависит от предпочтений и условий задачи. У каждого из этих способов свои преимущества и недостатки, поэтому важно выбрать наиболее удобный и подходящий метод в каждой конкретной ситуации.
Практические примеры расчета модуля равнодействующих сил
Расчет модуля равнодействующих сил на тело может быть необходим при решении различных задач механики. Ниже приведены несколько практических примеров, которые помогут вам разобраться в этом вопросе.
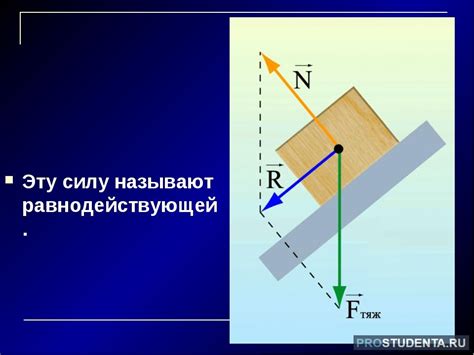
Пример 1: Уравновешивание тела на наклонной плоскости
Предположим, у вас есть тело массой 2 кг, которое находится на наклонной плоскости, образующей угол 30 градусов с горизонтом. Дано, что сила трения между телом и плоскостью составляет 10 Н. Требуется найти модуль равнодействующих сил на тело.
- Первым шагом найдем вес тела при помощи формулы: вес = масса * ускорение свободного падения. В нашем случае, вес равен: 2 * 9.8 = 19.6 Н.
- Затем найдем проекцию силы тяжести по направлению наклонной плоскости: вес * sin(30) = 19.6 * sin(30) ≈ 9.8 Н.
- Наконец, найдем модуль равнодействующих сил, который равен сумме проекции силы тяжести и силы трения: 9.8 + 10 = 19.8 Н.
Пример 2: Движение тела по горизонтальной поверхности
Предположим, у вас есть тело массой 5 кг, которое движется по горизонтальной поверхности. Известно, что на тело действует сила тяжести, равная 49 Н, и сила трения, равная 20 Н. Требуется найти модуль равнодействующих сил на тело.
- Сначала найдем силу трения, которая действует в противоположном направлении движения: 20 Н.
- Затем найдем модуль равнодействующих сил, который равен разности силы тяжести и силы трения: 49 - 20 = 29 Н.
Пример 3: Тело на вертикальной поверхности
Предположим, у вас есть тело массой 3 кг, которое находится на вертикальной поверхности. Сила трения между телом и поверхностью составляет 15 Н. Требуется найти модуль равнодействующих сил на тело.
- В данном случае, наклонная плоскость равна 90 градусов, поэтому проекция силы тяжести равна нулю.
- Таким образом, модуль равнодействующих сил равен силе трения, то есть 15 Н.
Это лишь несколько примеров расчета модуля равнодействующих сил на тело. Кроме того, существуют и другие методы и формулы для решения этих задач. Однако, основная идея заключается в нахождении суммы или разности действующих сил на тело в определенном направлении.
Помните, что правильное понимание и применение расчета модуля равнодействующих сил является важным навыком при изучении и применении механики в реальных ситуациях.
Итак, нашим главным заданием было найти модуль равнодействующих сил на тело. Мы изучили основные понятия и формулы, необходимые для этого расчета.
Первым шагом было разложение сил на составляющие, затем мы определяли направление и модуль каждой составляющей. После этого мы использовали теорему Пифагора для нахождения модуля равнодействующих сил на тело.
Важно помнить, что силы, действующие на тело, могут быть как параллельными, так и непараллельными. При расчете равнодействующей силы на тело, мы также должны учесть взаимное влияние сил.
Таким образом, после проведения всех необходимых расчетов, мы получаем модуль равнодействующих сил на тело - это величина, которая указывает на силу, действующую на тело в определенном направлении.
Знание и умение применять эти методы и формулы позволят нам более точно анализировать и понимать движение тела в различных ситуациях.
Будьте внимательны и аккуратны при расчетах, и помните, что практика - лучший способ научиться!