Призма - один из основных геометрических объектов, с которым мы сталкиваемся в школьной программе по математике. При этом, понять, как найти объем призмы, может быть не так просто на первый взгляд. Однако, существует простая формула, позволяющая рассчитать объем данной геометрической фигуры. В данной статье мы рассмотрим эту формулу и приведем примеры расчета объема призмы.
Объем призмы можно определить с использованием формулы V = S * h, где V - объем призмы, S - площадь основания и h - высота призмы. С другой стороны, площадь основания можно вычислить, зная его форму. Например, если основание призмы имеет форму квадрата со стороной a, то площадь основания будет равна S = a * a = a^2. Если же основание призмы имеет форму прямоугольника, то площадь основания будет равна S = a * b, где a и b – длины сторон прямоугольника.
Для того чтобы найти объем призмы, необходимо умножить площадь основания на ее высоту. Данный простой и понятный подход позволяет быстро и точно рассчитать объем данной геометрической фигуры. В данной статье мы рассмотрели основные моменты, связанные с расчетом объема призмы. Помните, что площадь основания и высота призмы являются ключевыми параметрами для определения объема данной геометрической фигуры.
Определение и свойства призмы
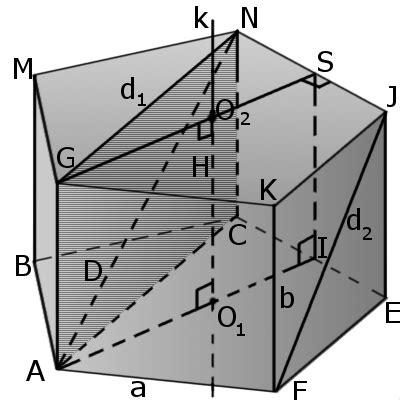
У призмы есть несколько свойств:
1. Основания призмы параллельны и равны друг другу, то есть имеют одинаковую форму и площадь.
2. Боковые грани призмы представляют собой прямоугольные параллелограммы, у которых длина стороны, соединяющей основания, называется высотой призмы.
3. Высота призмы перпендикулярна плоскости основания и равна расстоянию между двумя параллельными основаниями.
4. Объем призмы можно найти, умножив площадь основания на высоту: V = S * h, где V - объем, S - площадь основания, h - высота призмы.
5. Призмы бывают различных форм и размеров. Примерами призм являются куб, прямоугольная призма, треугольная призма и т. д.
6. Призмы широко используются в геометрии и строительстве. Они помогают решать задачи по нахождению объемов и площадей тел.
Формула для вычисления объема призмы
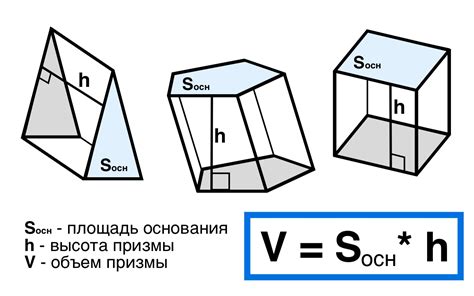
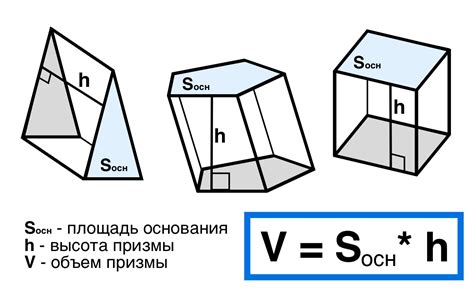
Объем призмы можно вычислить с помощью следующей формулы:
V = S * h
Где:
V - объем призмы;
S - площадь основания призмы;
h - высота призмы.
Для вычисления объема призмы необходимо найти площадь основания призмы и умножить ее на высоту. Площадь основания зависит от формы основания призмы и может быть найдена с помощью соответствующей формулы для каждой конкретной фигуры.
Шаги для расчета объема призмы
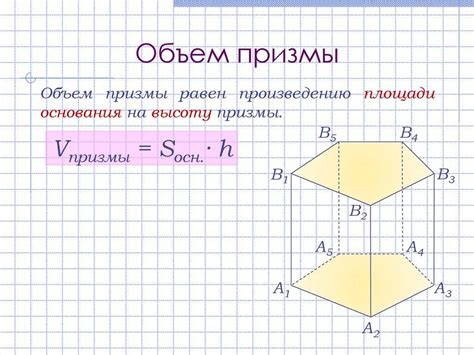
Для расчета объема призмы нужно выполнить следующие шаги:
1. Измерьте длину, ширину и высоту призмы.
Используйте линейку или измерительную ленту, чтобы измерить каждое измерение призмы. Обычно длина и ширина измеряются в метрах или сантиметрах, а высота - в метрах.
2. Умножьте длину, ширину и высоту призмы, чтобы найти объем основы.
Умножьте длину на ширину, а затем умножьте результат на высоту призмы. Это даст вам объем основы призмы в кубических единицах измерения.
Объем призмы = длина × ширина × высота.
3. Учитывайте подразделения измерения.
Если ваше измерение призмы было в сантиметрах, умножьте результат на 0,01, чтобы получить объем в метрах кубических.
4. Учитывайте форму призмы.
Если ваша призма имеет форму другого геометрического тела, используйте соответствующую формулу для расчета объема. Например, для прямоугольной призмы объем равен площади основы, умноженной на высоту.
Пользуясь этими шагами, вы сможете легко и точно рассчитать объем любой призмы и использовать эту информацию для решения различных задач и задач по геометрии.
Пример вычисления объема призмы
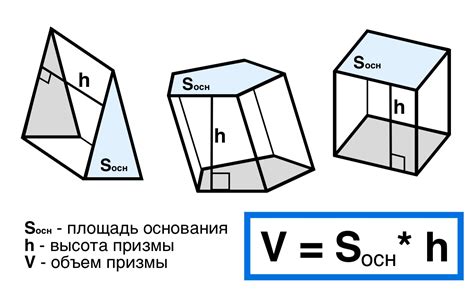
Рассмотрим конкретный пример вычисления объема призмы. Предположим, что у нас есть правильная треугольная призма с основанием, состоящим из равнобедренного треугольника со стороной равной 4 см и высотой 6 см. Также предположим, что высота призмы равна 10 см.
Для начала, найдем площадь основания призмы. Площадь равнобедренного треугольника можно найти по формуле:
S = (a * h) / 2,
где a - длина стороны треугольника, h - высота треугольника. Подставив значения из нашего примера, получим:
S = (4 * 6) / 2 = 12 см².
Теперь, учитывая найденную площадь основания и высоту призмы, можем вычислить объем призмы по формуле:
V = S * h,
где S - площадь основания призмы, h - высота призмы. Подставив значения из нашего примера, получим:
V = 12 см² * 10 см = 120 см³.
Таким образом, объем нашей призмы составляет 120 кубических сантиметров.
Практическое применение формулы для расчета объема призмы
Рассмотрим несколько примеров практического применения формулы для расчета объема призмы:
Пример 1: У вас есть школьный ящик, размеры которого составляют 30 см (длина), 20 см (ширина) и 15 см (высота). Какой объем занимает этот ящик?
Для решения этой задачи нужно воспользоваться формулой для объема прямоугольной призмы: V = a * b * c, где a, b и c - это длина, ширина и высота соответственно.
Подставляя значения из задания в формулу, получаем: V = 30 см * 20 см * 15 см = 9000 см³. Таким образом, объем школьного ящика составляет 9000 кубических сантиметров.
Пример 2: Вы планируете построить бассейн в форме прямоугольной призмы с длиной 5 метров, шириной 4 метра и глубиной 2 метра. Какой объем будет иметь ваш бассейн?
Используем ту же формулу для расчета объема прямоугольной призмы: V = a * b * c.
Подставляя значения из задания, получаем: V = 5 м * 4 м * 2 м = 40 м³. Таким образом, ваш бассейн будет иметь объем в 40 кубических метра.
Как видно из этих примеров, знание формулы для расчета объема призмы позволяет легко и быстро решать задачи, связанные с определением объема трехмерных фигур. Это очень полезное математическое понятие, которое может быть применено в различных сферах деятельности.