Опп в статистике – это обратная вероятность. Опп используется для нахождения вероятности события, дополняющего другое событие. Нахождение опп может быть полезно для решения различных задач, связанных с анализом данных, прогнозированием или оценкой рисков.
Существует несколько различных способов и методов, которые помогут вам найти опп в статистике. Один из самых простых способов – использование формулы опп. Суть этого метода заключается в нахождении вероятности дополнения события с помощью вычитания данной вероятности из единицы.
Другим методом для нахождения опп в статистике является использование таблиц или диаграмм. Таблицы и диаграммы могут помочь визуализировать данные и наглядно показать соотношение вероятностей различных событий. На основе этих данных вы можете легко найти опп и использовать его для принятия решений или сравнения различных вариантов.
Независимо от выбранного метода, важно помнить, что опп в статистике является всего лишь одним из инструментов для анализа данных. Чтобы его правильно применять, необходимо уметь оценить вероятности и связи между событиями, а также учитывать контекст и особенности конкретной задачи.
Анализ данных и выбор подходящих методов

Наиболее распространенные методы анализа данных включают:
Дескриптивный анализ данных - данный метод позволяет получить обобщенное представление о наборе данных, выявить основные закономерности и статистические характеристики.
Корреляционный анализ - данный метод позволяет оценить силу и направление взаимосвязей между переменными. Он позволяет выявить наличие или отсутствие корреляции и определить ее характер.
Регрессионный анализ - данный метод позволяет оценить влияние одной или нескольких независимых переменных на зависимую переменную. Он позволяет построить математическую модель и предсказать значения зависимой переменной на основе значений независимых переменных.
Анмова (анализ дисперсии) - данный метод позволяет оценить статистическую значимость различий между группами. Он широко используется для сравнения средних значений в нескольких группах или условиях.
Кластерный анализ - данный метод позволяет выявить группы или кластеры схожих объектов на основе сходства между ними. Он часто применяется в маркетинге и социологии для сегментации клиентов и аудитории.
Помимо указанных методов, существует еще множество других, таких как факторный анализ, дискриминантный анализ, временные ряды и т. д. Выбор конкретного метода анализа данных определяется исследуемой проблемой, доступностью данных, целями и гипотезами исследования.
Важно подчеркнуть, что правильный выбор метода анализа данных требует глубокого понимания статистических методов и отличное знание предметной области исследования.
Создание исследовательского плана и определение цели

Первым шагом в создании исследовательского плана является определение основной цели исследования. Цель может быть сформулирована в виде вопросов или утверждений, которые необходимо исследовать и проверить с помощью статистических методов.
Определение цели исследования требует четкости и конкретности. Цель должна быть измеримой, чтобы можно было определить, достигнута ли она в результате проведенного исследования. Также цель должна быть релевантной, то есть иметь практическую значимость и использоваться для разработки рекомендаций или принятия решений.
После определения цели исследования необходимо разработать исследовательский план, который будет помогать достичь этой цели. Исследовательский план включает в себя выбор методологии, определение выборки, сбор и анализ данных, а также интерпретацию результатов.
Выбор методологии зависит от характера исследования и целей, а также от доступных ресурсов и времени. Методология может включать в себя определение типа данных, подхода исследования (корреляционного, сравнительного и т. д.), а также выбор статистических методов для анализа данных.
Выбор образца или выборки также важен в статистическом исследовании. Образец должен быть репрезентативным и давать надежные результаты. Различные методы выборки могут использоваться, такие как случайная выборка или стратифицированная выборка.
Сбор и анализ данных – это следующий этап в исследовательском плане. Необходимо определить, какие данные нужно собрать, и как их анализировать с помощью статистических методов. Анализ данных может включать в себя описательную статистику, тестирование гипотез, регрессионный анализ и другие методы.
Создание исследовательского плана и определение цели исследования играют важную роль в статистическом исследовании. План помогает систематизировать процесс исследования и достигнуть поставленных целей. Четко определенные цели позволяют сфокусироваться на ключевых вопросах и проблемах, а также разработать рекомендации и принять обоснованные решения на основе полученных результатов.
Использование репрезентативной выборки
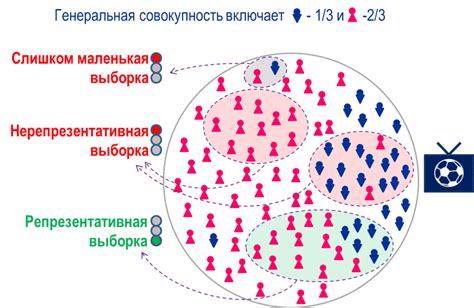
Репрезентативная выборка представляет собой подмножество данных, которое хорошо представляет основную генеральную совокупность. Для того чтобы выборка была репрезентативной, важно учесть следующие факторы:
1. Случайность: Выборка должна быть случайной, то есть каждый элемент генеральной совокупности должен иметь одинаковую вероятность попасть в выборку. Это поможет избежать искажений и убедиться, что выборка будет отражать разнообразие данных.
3. Профиль: Репрезентативная выборка должна быть сбалансированной и отображать профиль генеральной совокупности. Например, если интересующая нас группа состоит из 60% мужчин и 40% женщин, выборка должна соответствовать этим пропорциям.
Использование репрезентативной выборки позволяет получить достоверные и репрезентативные результаты, при этом экономя время и ресурсы. Это особенно важно при проведении опросов, маркетинговых исследований, а также при анализе социальных и экономических данных.
Важно помнить, что репрезентативная выборка не является идеальной, и ее использование может иметь некоторые ограничения и остаточные ошибки. Однако, с правильным подходом и учетом всех факторов, она может быть полезным инструментом в работе статистика.
Определение показателей и переменных для изучения

Для определения опп необходимо учитывать цель исследования, а также иметь понимание о предмете изучения. Переменные, которые будут включены в опп, должны быть измеримыми и иметь статистическую значимость в контексте исследуемой проблемы.
Изучение опп включает следующие шаги:
- Анализ цели исследования и формулирование вопросов, которые требуют ответов.
- Поиск информации и литературы по теме исследования, изучение существующих переменных и показателей.
- Выбор основных переменных и показателей, которые наиболее полно отражают характеристики исследуемого явления.
- Изучение методов сбора данных для определения возможности измерения выбранных показателей и переменных.
- Организация сбора данных и обработка полученных результатов.
Определение опп позволяет структурировать процесс исследования и обеспечить точность и достоверность результатов. Оптимальный выбор переменных и показателей позволяет получить полноценную информацию о изучаемом явлении и дает возможность принять обоснованные решения на основе полученных данных.
Перекрестная проверка и кросс-валидация
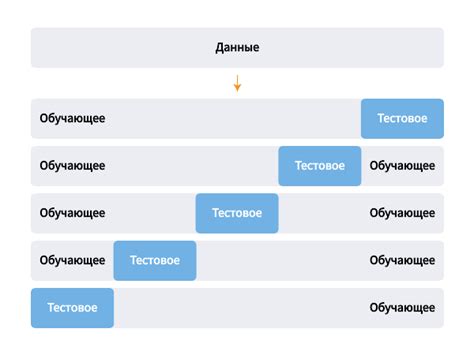
Перекрестная проверка представляет собой процесс разбиения доступных данных на обучающую и тестовую выборки. Обучающая выборка используется для построения модели, а тестовая выборка используется для оценки ее качества. Такой подход позволяет учитывать вариации в данных и уменьшает вероятность переобучения модели.
Одним из распространенных методов перекрестной проверки является k-блочная перекрестная проверка. Данные разбиваются на k равных блоков, и каждый блок последовательно используется в качестве тестовой выборки, а оставшиеся блоки - в качестве обучающей выборки. Таким образом, каждый блок используется как тестовая выборка ровно один раз.
Кросс-валидация представляет собой процесс повторения перекрестной проверки несколько раз с разными разбиениями данных. Это помогает получить более устойчивые оценки качества модели, так как разбиение данных может влиять на результаты.
После завершения перекрестной проверки или кросс-валидации можно оценить качество модели с использованием различных метрик, таких как точность, полнота, F1-мера и т. д. Также можно провести статистические тесты для определения значимости различий между разными моделями или параметрами.
Применение регрессии и корреляционного анализа
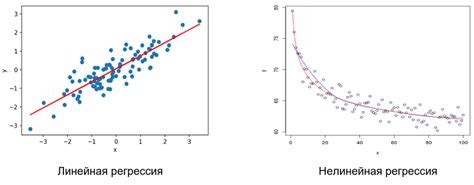
Регрессионный анализ используется для предсказания значения одной переменной (зависимой) на основе другой или нескольких других (независимых) переменных. Он позволяет установить, какие переменные оказывают значительное влияние на результат и каким образом изменение значений независимых переменных влияет на зависимую переменную. Регрессионный анализ может быть применен в различных областях, например, для прогнозирования продаж или оценки влияния рекламной кампании на продуктовый спрос.
Корреляционный анализ, в свою очередь, позволяет определить степень связи между двумя или более переменными. Он позволяет выявить, есть ли статистически значимая связь между переменными, и какая именно это связь (положительная или отрицательная). Корреляционный анализ часто применяется в исследованиях социальных наук, экономике, медицине и других областях, где важно понять, как взаимосвязаны различные факторы.
Применение регрессии и корреляционного анализа позволяет не только найти опп в статистике, но и обосновать эти результаты с помощью числовых показателей. Важно помнить, что корреляция не означает причинно-следственную связь, а лишь указывает на степень связи между переменными. Регрессия же позволяет выявить влияние независимых переменных на зависимую с учетом других факторов. Эти методы являются мощными инструментами статистического анализа и могут применяться для решения различных задач в научных исследованиях и практическом бизнесе.
Использование статистических тестов

Для нахождения опп в статистике широко применяются различные статистические тесты. Они позволяют оценить вероятность различий между группами и определить наличие статистически значимых результатов.
Одним из наиболее распространенных тестов является t-тест. Данный тест позволяет сравнить средние значения двух групп и определить, есть ли между ними статистически значимые различия. T-тест используется, когда данные распределены нормально и имеют равные дисперсии.
Еще одним распространенным статистическим тестом является анализ дисперсии (ANOVA). ANOVA позволяет сравнить средние значения трех и более групп и определить, есть ли между ними статистически значимые различия. Данный тест используется, когда данные распределены нормально и имеют равные дисперсии.
Для категориальных данных часто используется хи-квадрат тест. Он позволяет оценить связь и зависимость между двумя категориальными переменными. Хи-квадрат тест также может быть применен для проверки гипотез о равенстве распределений между группами.
Для более сложных и специфических случаев существуют и другие статистические тесты, такие как доверительные интервалы, корреляционный анализ, регрессионный анализ и другие. Выбор конкретного теста зависит от типа данных, гипотезы, которую необходимо проверить, и цели исследования.
Важно помнить, что использование статистических тестов требует правильной интерпретации результатов и определения статистической значимости. Кроме того, необходимо учитывать возможные ограничения и предпосылки каждого теста, чтобы выбрать наиболее подходящий метод анализа данных.
Интерпретация результатов и оценка их значимости

Один из наиболее распространенных способов оценки значимости результатов - проведение гипотезного тестирования. Этот метод позволяет проверить, есть ли статистически значимое различие между группами или переменными. В результате тестирования получаются p-значения, которые интерпретируются как вероятность получения таких или более экстремальных результатов при условии справедливости нулевой гипотезы. Если p-значение меньше выбранного уровня значимости (обычно 0.05), то различие считается статистически значимым.
Однако, важно помнить, что статистическая значимость не всегда соответствует практической значимости. Например, если наблюдается небольшое статистически значимое различие между двумя группами, это может быть незначительным с практической точки зрения. В таких случаях необходимо применять дополнительные методы оценки практической значимости, такие как определение размера эффекта или проведение доверительных интервалов.
Визуализация данных с помощью графиков и диаграмм

Один из наиболее распространенных типов графиков - это график линий. Он отображает зависимость между двумя переменными во времени. График линий может быть использован, например, для анализа изменения цены на товары или акции.
Другим распространенным типом графика является столбчатая диаграмма. Она позволяет сравнивать значения разных категорий и наглядно показывает различия между ними. Столбчатые диаграммы могут быть использованы, например, для сравнения продаж разных товаров или доходов разных регионов.
Круговая диаграмма - еще один популярный тип графика, который позволяет показать соотношение разных категорий относительно целого. Круговая диаграмма часто используется для представления процентного соотношения, например, подсчета доли мужчин и женщин в определенной группе.
С помощью графиков и диаграмм можно создать комплексные визуализации данных, объединяя разные типы графиков и добавляя дополнительные элементы, такие как подписи осей, легенды и заголовки. Визуализация данных не только помогает лучше понять и проанализировать статистическую информацию, но и делает ее более привлекательной и интересной для аудитории.
Сравнение различных методов и выбор наиболее эффективного

Один из популярных методов - точечная оценка опп. Этот метод представляет собой расчет отношения положительного к отрицательному на основе наблюдаемых значений. Однако он не учитывает возможные погрешности и имеет ограниченную применимость, особенно при работе с небольшими выборками.
Второй метод - доверительный интервал опп. Он позволяет оценить диапазон, в котором с определенной вероятностью находится истинное значение опп. Доверительный интервал учитывает погрешность выборки и даёт более надежные результаты, особенно при использовании больших выборок.
Третий метод - хи-квадрат тест. Он используется для сравнения фактических наблюдаемых значений с ожидаемыми значениями в случае, когда нет независимости между переменными. Хи-квадрат тест может быть эффективным методом для нахождения опп в таких случаях, но требует подготовки соответствующих таблиц и проверки гипотез.
Выбор наиболее эффективного метода зависит от конкретной задачи и доступных данных. Если имеются большие выборки и интересует оценка диапазона опп, то рекомендуется использовать доверительный интервал опп. Если же наблюдается зависимость между переменными, то хи-квадрат тест может быть лучшим вариантом.
Идеального метода для нахождения опп не существует, и выбор метода следует основывать на целях и требованиях исследования. Важно также учитывать возможные ограничения и погрешности каждого метода, чтобы получить более точные и надежные результаты.