Трапеция - одна из наиболее известных и широко используемых геометрических форм. Она имеет множество применений в различных областях знания, включая инженерию, архитектуру, строительство и многое другое. Основание и высота трапеции - два основных элемента, которые определяют ее форму и свойства. В этой статье мы рассмотрим, как найти основание и высоту трапеции и приведем несколько примеров для наглядности.
Основание трапеции - это отрезок, который соединяет оба параллельных стороны фигуры. Он обычно обозначается буквой "а" или "б". Чтобы найти основание трапеции, необходимо знать длины параллельных сторон и другие известные параметры. В некоторых случаях основание может быть неявно задано, например, если известны только углы трапеции.
Высота трапеции - это перпендикуляр, опущенный из вершины фигуры к основанию. Она обычно обозначается буквой "h". Высота трапеции может быть найдена различными способами в зависимости от известных параметров. Например, если известны длины оснований и площадь трапеции, то высота может быть вычислена по формуле "h = 2S / (a + b)", где "S" - площадь, "a" и "b" - длины оснований.
Узнайте основные понятия трапеции и их особенности
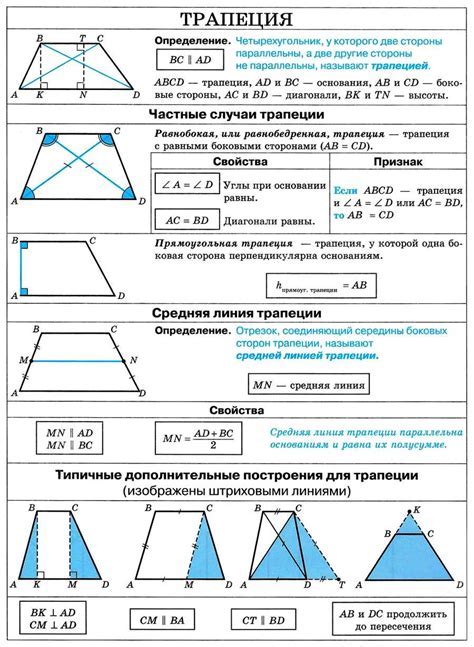
| Название | Описание |
|---|---|
| Основание | Основания трапеции - это две параллельные стороны. Обычно их обозначают буквами "а" и "b". |
| Высота | Высота трапеции - это отрезок, проведенный перпендикулярно основаниям. Обычно обозначается буквой "h". |
| Боковые стороны | Боковые стороны трапеции - это две непараллельные стороны. |
| Углы | Трапеция имеет два пары противолежащих углов. Углы, образованные основаниями и боковыми сторонами, называются основными углами. Углы, образованные боковыми сторонами, называются боковыми углами. |
Основная особенность трапеции заключается в том, что сумма длин любых ее двух сторон всегда больше, чем сумма длин оставшихся двух сторон. Также, сумма углов в трапеции всегда равна 360 градусов.
Знание основных понятий и особенностей трапеции поможет вам легче понять и решать задачи, связанные с этой фигурой.
Советы и инструкции по определению основания и высоты трапеции

1. Для того чтобы найти основание трапеции, обратите внимание на ее форму. Основание трапеции - это параллельные стороны фигуры. Измерьте длины этих сторон с помощью линейки или другого подходящего инструмента.
2. Высота трапеции - это перпендикулярное расстояние между основаниями. Измерьте это расстояние, используя уровень или другой инструмент для измерения перпендикуляра.
3. Если вам даны значения длин двух непараллельных сторон трапеции и ее высоты, вы можете использовать формулу для вычисления площади трапеции: S = (a + b) * h / 2, где a и b - длины оснований, h - высота.
4. Если вам даны значения площади трапеции и ее высоты, а также одно из оснований, вы можете использовать формулу для нахождения другого основания: b = 2 * S / h - a, где b - второе основание, a - первое основание, h - высота.
5. Помните, что в зависимости от задачи и известных данных могут использоваться и другие формулы для нахождения основания и высоты трапеции. Убедитесь в правильности выбора формулы перед применением ее для решения задачи.
6. При нахождении основания и высоты трапеции важно быть внимательным и точным при измерениях. Малейшая ошибка может привести к неправильным результатам.
Следуя этим советам и инструкциям, вы сможете определить основание и высоту трапеции и успешно решить любую задачу, связанную с этой геометрической фигурой.
Примеры расчета основания и высоты трапеции
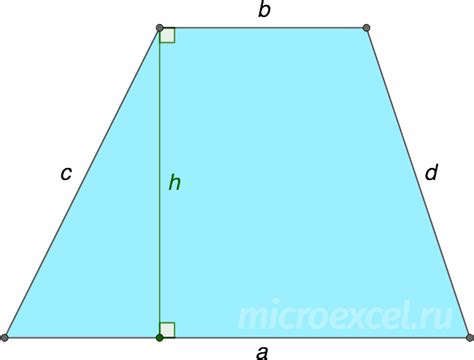
Для расчета основания и высоты трапеции необходимо знать длины ее боковых сторон и диагонали. Рассмотрим несколько примеров:
Пример 1:
Для трапеции ABCD известны следующие значения:
- Сторона AB = 8 см
- Сторона CD = 12 см
- Диагональ AC = 10 см
Найдем основание трапеции:
Основание трапеции можно найти как разность длин боковых сторон. В данном случае основание трапеции равно:
AB - CD = 8 см - 12 см = -4 см
В данном примере получили отрицательную длину основания. Это означает, что мы допустили ошибку в измерениях или в расчетах.
Найдем высоту трапеции:
Высоту трапеции можно найти с помощью теоремы Пифагора. Для этого найдем значение боковой стороны BC:
BC2 = AC2 - AB2 = 10 см2 - 8 см2 = 36 см2
BC = √36 см = 6 см
Высота трапеции равна расстоянию между параллельными сторонами. Она будет равна длине боковой стороны BC, то есть:
Высота = 6 см
Пример 2:
Для трапеции XYZW известны следующие значения:
- Сторона XY = 5 см
- Сторона ZW = 7 см
- Диагональ YZ = 8 см
Найдем основание трапеции:
AB - CD = XY - ZW = 5 см - 7 см = -2 см
Опять получили отрицательную длину основания, что свидетельствует об ошибке в измерениях или в расчетах.
Найдем высоту трапеции:
BC2 = AC2 - XY2 = 8 см2 - 5 см2 = 39 см2
BC = √39 см ≈ 6,24 см
Высота трапеции равна длине боковой стороны BC, то есть:
Высота ≈ 6,24 см
В этих примерах мы увидели, что при неправильных измерениях или некорректных расчетах значения основания могут быть отрицательными. В таких случаях необходимо повторить измерения и проверить расчеты.