Четырехугольники – это фигуры с четырьмя сторонами. Их разнообразие поражает – от прямоугольников до трапеций, каждый имеет свои особенности. Однако, для определения его характеристик, таких как площадь и периметр, мы выполняем одни и те же действия.
Периметр четырехугольника – это сумма длин всех его сторон. Чтобы найти периметр, нужно просуммировать все стороны фигуры. Если стороны четырехугольника равны, то его периметр можно найти, умножив длину одной стороны на 4.
Для подсчета площади четырехугольника необходимо знать его формулу. Существуют различные способы нахождения площади в зависимости от вида фигуры. Например, для прямоугольника площадь равна произведению длины одной из его сторон на длину противоположной стороны. В случае, если известна высота прямоугольника, площадь можно найти, умножив высоту на длину.
Однако, существует много других видов четырехугольников, включая ромб, квадрат, параллелограмм и трапецию. Для расчета площади этих фигур применяются свои специфические формулы. Значит, чтобы быть в полной готовности к вычислениям, важно знать формулы для каждого типа четырехугольника.
В данной статье мы рассмотрим основные типы четырехугольников и покажем, как найти периметр и площадь каждого из них. Это поможет вам усовершенствовать ваши навыки математических вычислений и успешно решать задачи, связанные с этим видом геометрии.
Периметр четырехугольника: основные принципы расчета
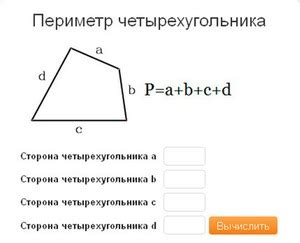
Для прямоугольника и квадрата периметр можно найти по формуле: Периметр = 2 * (Длина + Ширина). В этих случаях достаточно знать длину и ширину объекта. Но если стороны разные, нужно поступить иначе.
Если четырехугольник не является прямоугольником или квадратом, его периметр можно найти, сложив длины всех его сторон: Периметр = Длина_a + Длина_b + Длина_c + Длина_d. Важно помнить, что порядок сложения сторон не имеет значения – сумма будет одинакова в любом случае.
Существуют специальные случаи четырехугольников, для которых существуют более простые формулы расчета периметра. Например, для равнобедренной трапеции, периметр можно найти следующим образом: Периметр = Длина_основания_a + Длина_основания_b + 2 * Длина_боковой_стороны.
Важно помнить, что периметр – это внешняя граница четырехугольника, длины всех его сторон. Расчет периметра основывается на знании длин сторон и специфике формы четырехугольника.
Методы определения сторон и суммирования
Для определения сторон и суммирования периметра и площади четырехугольника существует несколько методов, которые позволяют получить точный результат.
Использование формулы для вычисления периметра и площади является наиболее распространенным методом. Для этого необходимо знать длину каждой стороны четырехугольника. Для расчета периметра нужно сложить длины всех сторон, а для расчета площади можно использовать формулу Герона или другую соответствующую формулу.
Если длины сторон четырехугольника неизвестны, можно воспользоваться методом их определения с помощью геометрической конструкции. Для этого нужно построить перпендикуляры к соединяющим его противолежащим сторонам, а затем измерить получившиеся отрезки. Суммируя эти отрезки, можно получить периметр четырехугольника.
| Метод | Преимущества | Недостатки |
|---|---|---|
| Использование формулы | Точный результат | Необходимость знания длин всех сторон |
| Геометрическая конструкция | Возможность определения длин сторон | Большая сложность визуального определения |
В зависимости от конкретной задачи и доступных исходных данных можно выбрать наиболее подходящий метод для определения сторон и суммирования периметра и площади четырехугольника. Важно помнить, что результаты расчетов могут быть точными только при точных исходных данных, поэтому необходимо обращать внимание на точность измерений и использовать проверенные методы.
Формулы и алгоритмы для разных видов четырехугольников

Прежде чем приступать к расчету площади и периметра четырехугольника, необходимо учитывать его тип и свойства. В этом разделе мы рассмотрим формулы и алгоритмы для разных видов четырехугольников, чтобы вы могли правильно выполнить расчеты.
| Тип четырехугольника | Формула для расчета площади | Формула для расчета периметра |
|---|---|---|
| Прямоугольник | Площадь = длина * ширина | Периметр = 2 * (длина + ширина) |
| Квадрат | Площадь = сторона * сторона | Периметр = 4 * сторона |
| Ромб | Площадь = (диагональ1 * диагональ2) / 2 | Периметр = 4 * сторона |
| Трапеция | Площадь = (основание1 + основание2) * высота / 2 | Периметр = сторона1 + сторона2 + сторона3 + сторона4 |
Здесь длина, ширина, сторона, основание и высота - это измерения соответственных сторон и размеров четырехугольника. Диагональ1 и диагональ2 - это диагонали ромба, сторона1, сторона2, сторона3 и сторона4 - стороны трапеции.
Расчет площади и периметра разных видов четырехугольников осуществляется путем применения соответствующих формул. Следует заметить, что это лишь некоторые из возможных видов четырехугольников, и каждый из них имеет свои особенности и условия расчета.
Точное знание формул и алгоритмов для разных видов четырехугольников позволяет правильно провести математические расчеты и получить нужные результаты. Не забывайте учитывать единицы измерения при выполнении вычислений и округлять числа, если необходимо.
Площадь четырехугольника
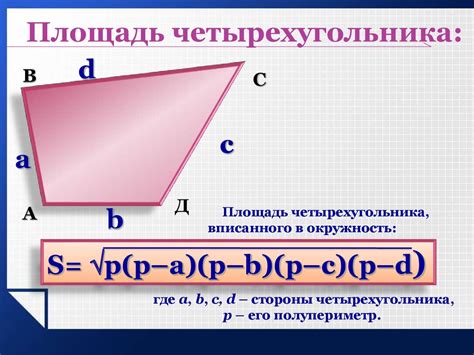
Для расчета площади четырехугольника необходимо знать его стороны и углы. Существует несколько способов расчета площади в зависимости от доступных данных.
Если известны все стороны четырехугольника, можно воспользоваться формулой Гаусса:
| S = sqrt((p - a) * (p - b) * (p - c) * (p - d)) |
где S - площадь, a, b, c, d - стороны четырехугольника, p - полупериметр, который может быть вычислен по формуле:
| p = (a + b + c + d) / 2 |
Если известны диагонали и угол между ними, площадь четырехугольника можно вычислить по формуле:
| S = (d1 * d2 * sin(angle)) / 2 |
где S - площадь, d1 и d2 - диагонали, angle - угол между ними.
Если известны длины баз и высоты, площадь четырехугольника можно вычислить по формуле:
| S = (a + b) * h / 2 |
где S - площадь, a и b - длины баз, h - высота.
Важно помнить, что для правильного расчета площади необходимо учитывать единицы измерения и выполнять соответствующие преобразования, если необходимо.
Способы вычисления площади разных типов четырехугольников
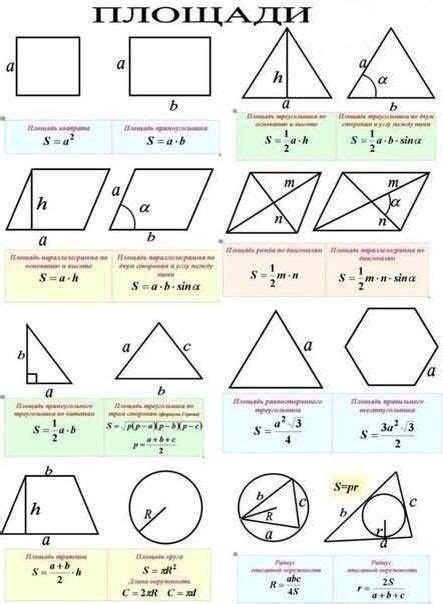
Четырехугольники делятся на несколько типов: прямоугольники, квадраты, параллелограммы, трапеции и ромбы. Для вычисления площади этих фигур существуют различные методы.
Для прямоугольников и квадратов площадь можно найти, умножив длину одной стороны на длину другой. Это самый простой способ, так как все стороны этих фигур равны.
Параллелограммы имеют две пары параллельных сторон и равные углы у оснований. Площадь такого четырехугольника можно найти, умножив длину одной стороны на высоту, опущенную к этой стороне.
Трапеции имеют одну пару параллельных сторон и две неравные. Для вычисления площади трапеции нужно сложить длины двух параллельных сторон, умножить получившуюся сумму на высоту трапеции, а затем разделить результат на 2.
Ромбы имеют все стороны равной длины. Площадь ромба можно найти, умножив длину одной стороны на высоту, опущенную к этой стороне.
Вычисление площади четырехугольников требует знания основных формул и свойств каждого типа фигур. Используя эти способы, вы сможете легко и точно найти площадь разных типов четырехугольников.