Узнать периметр геометрических фигур - одно из важных умений, которое дети обучаются в 4 классе. Когда речь идет о неровной фигуре, это может вызывать затруднения и запутанность учеников. Но не стоит беспокоиться! Сегодня мы расскажем, как легко и быстро вычислить периметр для неровной фигуры.
Периметр - это сумма длин всех сторон фигуры. Если фигура имеет несколько углов и сторон различной длины, найти периметр может показаться сложной задачей. Однако, с помощью нескольких простых шагов, вы сможете справиться с этой задачей без проблем.
Первым шагом является внимательное осмотрение фигуры. Вам необходимо найти все стороны фигуры и записать их длину. Не забудьте обратить внимание на то, какие стороны параллельны между собой, так как они могут иметь одинаковую длину. Если вам кажется, что фигура слишком сложна, вы можете разбить ее на более простые фигуры и вычислить их периметры отдельно.
Когда вы найдете все стороны фигуры, сложите их длины и получите периметр неровной фигуры. Не забудьте проверить свой результат. Если у вас есть сомнения, попросите учителя или родителей помочь вам. Повторите этот процесс для разных неровных фигур и вы станете настоящим экспертом в вычислении периметра!
Определение неровной фигуры и ее периметра
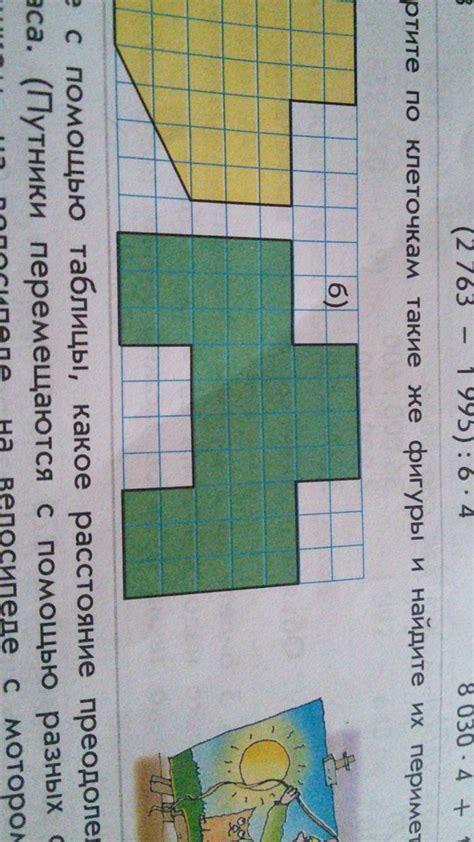
Периметр неровной фигуры - это сумма длин всех ее сторон. Для определения периметра необходимо измерить каждую сторону фигуры и сложить полученные значения. Если неровная фигура состоит из различных линий и углов, измерение и суммирование длин сторон может быть достаточно трудоемким процессом.
Для определения периметра неровной фигуры могут применяться различные методы и инструменты. Например, при измерении по плоскости можно использовать линейку или мерную ленту. При измерении трехмерных фигур можно применять специализированные инструменты, такие как лазерные измерители или компьютерные программы.
Важно помнить, что точность измерений влияет на точность определения периметра неровной фигуры. Поэтому необходимо использовать точные и надежные инструменты, а также следить за правильностью проведения измерений.
Зная периметр неровной фигуры, мы можем использовать эту информацию для решения различных задач. Например, вычислять площадь фигуры, определять необходимое количество материала для ее обработки или строительства.
Важно помнить
Измерение периметра неровной фигуры может потребовать некоторого времени и усилий. Важно использовать точные и надежные инструменты для достижения наибольшей точности измерений.
Будьте внимательны при проведении измерений и не допускайте ошибок, чтобы получить наиболее точные значения периметра неровной фигуры.
Как найти периметр неровной фигуры с помощью измерения сторон

Чтобы найти периметр неровной фигуры, следуйте этим простым шагам:
- Наберите необходимые измерения инструментом для измерения длины, например линейкой или мерной лентой.
- Расположите фигуру на ровной поверхности, чтобы верно измерить каждую сторону.
- Начните измерение с первой стороны фигуры. Приложите инструмент измерения к началу стороны и проведите его до конца, чтобы определить длину стороны.
- Продолжайте измерение каждой стороны по очереди, записывая длину каждой из них.
- Когда все стороны измерены, сложите их длины, чтобы получить периметр фигуры. Это будет ответ на задачу.
Например, пусть нам нужно найти периметр фигуры, состоящей из трех сторон со следующими длинами: 5 см, 7 см и 9 см. Просто сложите эти числа: 5 + 7 + 9 = 21. Периметр фигуры равен 21 см.
Теперь вы знаете, как найти периметр неровной фигуры с помощью измерения каждой стороны. Применяйте эти шаги к различным фигурам и решайте задачи!
Использование разделения фигуры на более простые части для вычисления периметра
Вычисление периметра неровной фигуры может быть сложной задачей для четвероклассников. Однако, с использованием метода разделения фигуры на более простые части, это задание может стать гораздо проще и понятнее.
Когда мы имеем дело с неровной фигурой, то можно выделить отдельные фигуры, какими они кажутся на первый взгляд. Например, если у нас есть фигура в форме буквы "П", то можно разделить ее на две отдельные прямоугольные фигуры.
После разделения фигуры, мы можем вычислить периметр каждой отдельной фигуры. После этого мы просто складываем все полученные значения периметров и получаем общий периметр фигуры.
Важно помнить, что при разделении фигуры на более простые части, мы не должны терять ни одного отрезка или фигуры. Если какая-то часть фигуры отсутствует, нужно убедиться, что ее периметр также учтен.
Теперь вы можете использовать этот метод для вычисления периметра любой неровной фигуры. Разделите ее на более простые части, вычислите периметр каждой части и сложите все результаты вместе. Таким образом, вы сможете успешно решать задачи, связанные с вычислением периметра неровных фигур.
Как найти периметр неровной фигуры с использованием графического метода на координатной плоскости

Для нахождения периметра неровной фигуры с использованием графического метода на координатной плоскости необходимо выполнить следующие шаги:
- Нанести фигуру на координатную плоскость с помощью точек, соединенных линиями.
- Измерить длины всех сторон фигуры с помощью линейки или с использованием единиц измерения на координатной плоскости.
- Сложить длины всех сторон фигуры, чтобы найти периметр.
Пример:
Представим, что у нас есть неровная фигура, которая состоит из пяти линий. Закрасим эту фигуру на координатной плоскости и измерим длины каждой линии с помощью линейки:
Линия AB = 3 см
Линия BC = 2 см
Линия CD = 4 см
Линия DE = 2 см
Линия EF = 3 см
Теперь сложим длины всех сторон фигуры, чтобы найти периметр:
Периметр = AB + BC + CD + DE + EF = 3 + 2 + 4 + 2 + 3 = 14 см
Итак, периметр данной фигуры равен 14 см.
Таким образом, графический метод на координатной плоскости позволяет найти периметр неровной фигуры путем измерения длин всех ее сторон и их сложения.
Работа с неровными фигурами в пространстве - как найти их периметр
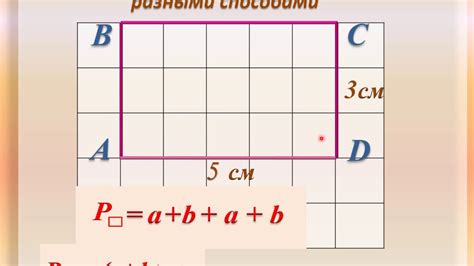
Для того чтобы найти периметр неровной фигуры, нам понадобится знание различных методов и приемов. Один из них – разбиение фигуры на более простые элементы, для которых можно легко вычислить периметр. После этого, найденные значения складываются вместе.
Но как разбить неровную фигуру на более простые элементы? Нам помогут различные геометрические фигуры: прямоугольники, треугольники, круги и другие. Мы можем приближенно описать фигуру с помощью таких фигур, вычислить их периметры и суммировать полученные значения.
Если границы неровной фигуры состоят из прямых линий и кривых, можно попробовать использовать метод аппроксимации, то есть заменить кривые линии прямыми. Таким образом, мы будем работать с прямоугольником или многоугольником, который с близкой точностью будет соответствовать исходной фигуре. Периметр такого приближенного прямоугольника или многоугольника будет приближенным значением периметра неровной фигуры.
Использование формул для вычисления периметра неровных фигур

Вычисление периметра неровной фигуры может показаться сложной задачей, но с использованием соответствующих формул это можно сделать в несколько простых шагов. Для разных типов неровных фигур существуют свои специальные формулы.
Для прямоугольников и квадратов вычисление периметра выполняется очень просто. Периметр прямоугольника равен сумме всех его сторон, а периметр квадрата равен удвоенному значению одной из его сторон. Например, если сторона прямоугольника равна 4 см, то его периметр будет равен 4 + 4 + 4 + 4 = 16 см.
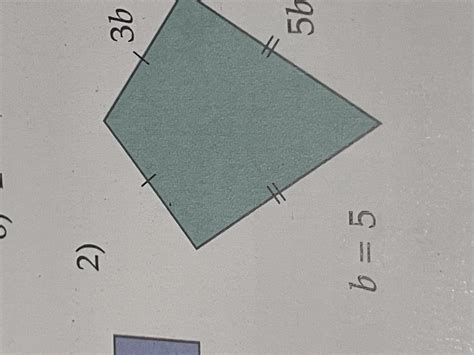
Для треугольников вычисление периметра немного сложнее. Периметр треугольника равен сумме длин всех его сторон. Если известны длины всех сторон треугольника, то просто их сложите. Например, если длины сторон треугольника равны 5 см, 7 см и 9 см, то периметр будет равен 5 + 7 + 9 = 21 см.
Для вычисления периметра круга, необходимо использовать формулу 2πr, где π (пи) – это математическая константа, приближенное значение которой равно 3.14, а r – радиус круга. Например, если радиус круга равен 6 см, то его периметр будет равен 2 * 3.14 * 6 = 37.68 см.
Для вычисления периметра других неровных фигур, таких как трапеция или многоугольник, необходимо использовать специальные формулы, которые могут быть более сложными. При наличии этих формул вычисление периметра будет не составлять большого труда.
Использование формул для вычисления периметра неровных фигур поможет вам быстро и точно определить длину контура фигуры. Важно помнить, что правильное применение формул исключает возможность ошибок при вычислении периметра.
Примеры задач на вычисление периметра неровных фигур для самостоятельного решения

Для того чтобы лучше разобраться в теме вычисления периметра неровных фигур, предлагается решить несколько примеров самостоятельно. Это поможет закрепить полученные знания и научиться применять их на практике.
1. На картинке изображена неровная фигура. Вам необходимо вычислить ее периметр. Фигура состоит из прямоугольника и треугольника. Длина одной стороны прямоугольника равна 5 см, а длина второй стороны равна 8 см. Основание треугольника имеет длину 4 см, а его высота – 6 см.
- Шаг 1: Найдите длину периметра прямоугольника с помощью формулы P = 2(a + b), где a и b – длины сторон прямоугольника.
- Шаг 2: Найдите периметр треугольника, сложив длины его сторон (основание и две равные стороны).
- Шаг 3: Сложите полученные значения периметров прямоугольника и треугольника, чтобы найти общий периметр фигуры.
2. На чертеже изображена неровная фигура, состоящая из нескольких треугольников и прямоугольников. Необходимо найти ее периметр. Известны длины сторон треугольников и прямоугольников: сторона прямоугольника равна 7 см, длина одной стороны треугольника – 3 см, длина второй стороны треугольника – 5 см.
- Шаг 1: Посчитайте периметр прямоугольника по формуле P = 2(a + b), где a и b – длины его сторон.
- Шаг 2: Вычислите периметр каждого треугольника, складывая длины его сторон.
- Шаг 3: Сложите полученные значения периметров треугольников и прямоугольника, чтобы найти общий периметр фигуры.
3. На рисунке изображена неровная фигура, состоящая из двух прямоугольников и двух треугольников. Требуется найти ее периметр. Длина одной стороны первого прямоугольника равна 4 см, а длина второй стороны – 6 см. Длина основания первого треугольника составляет 5 см, а высота – 3 см.
- Шаг 1: Подсчитайте периметр первого прямоугольника по формуле P = 2(a + b), где a и b – длины его сторон.
- Шаг 2: Вычислите периметр первого треугольника, складывая длины его сторон.
- Шаг 3: Посчитайте периметр второго прямоугольника и второго треугольника аналогично.
- Шаг 4: Добавьте полученные значения периметров прямоугольников и треугольников, чтобы получить общий периметр фигуры.
4. На чертеже изображена неровная фигура, состоящая из трех прямоугольников и двух треугольников. Необходимо найти ее периметр. Длина одной стороны первого прямоугольника равна 3 см, а длина второй стороны – 8 см. Длина одной стороны второго прямоугольника – 5 см, а длина второй стороны – 4 см. Длина основания третьего треугольника равна 6 см, а высота – 2 см.
- Шаг 1: Посчитайте периметр каждого прямоугольника по формуле P = 2(a + b), где a и b – длины его сторон.
- Шаг 2: Подсчитайте периметр каждого треугольника, складывая длины его сторон.
- Шаг 3: Сложите полученные значения периметров прямоугольников и треугольников, чтобы получить общий периметр фигуры.
Важность изучения и практического применения знаний о периметре неровных фигур

Изучение и практическое применение знаний о периметре неровных фигур важно, потому что:
- Позволяет оценить длину забора или трату материала: Если у вас есть сад или огород, знания о периметре помогут вам определить длину необходимого забора или оценить количество материала, требуемого для строительства.
- Помогает вычислить длину дороги: Зная периметр неровной фигуры, вы можете вычислить длину дороги, окружности стадиона или любой другой необычной формы объекта.
- Полезно в дизайне интерьера: Если вы планируете разместить мебель в комнате или рассчитать длину бортиков на столе, знание периметра поможет вам правильно спланировать расстановку предметов.
- Важно для построения карты: Геометрические знания о периметре позволяют строить карты, в том числе топографические, которые являются важной частью общественных и государственных проектов.