Шар, вписанный в пирамиду, представляет собой особый геометрический объект, привлекающий внимание своей симметрией и уникальными свойствами. Такой шар касается всех граней пирамиды и является важным элементом для решения различных геометрических задач. Если вам интересно узнать, как найти радиус шара, вписанного в пирамиду, то этот простой гид поможет вам разобраться в этом вопросе.
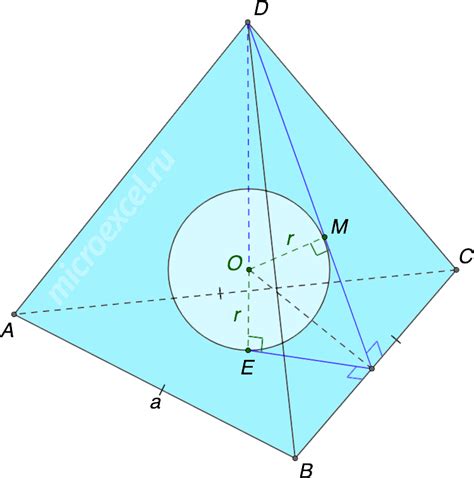
Прежде чем перейдем к расчетам, давайте вспомним некоторые основные определения. Пирамида – это многогранник, состоящий из многоугольника, называемого основанием пирамиды, и треугольных граней, называемых боковыми гранями. Вписанный шар – это шар, который полностью касается всех граней пирамиды. Известно, что центр вписанного шара совпадает с центром основания пирамиды, а его радиус является радиусом окружности, вписанной в основание.
Теперь перейдем к вычислению радиуса шара вписанного в пирамиду. Для этого необходимо воспользоваться следующей формулой: радиус шара равен произведению радиуса вписанной окружности основания и высоты пирамиды, деленному на сумму значения радиуса основания и значения радиуса шара. Эту формулу можно представить следующим образом:
Как найти радиус шара вписанного в пирамиду
Чтобы найти радиус шара, который вписан в пирамиду, нам понадобится знать высоту и площадь основания пирамиды. Для этого есть несколько простых шагов:
- Найдите площадь основания пирамиды. Обычно это прямоугольник, треугольник или многоугольник. Для прямоугольной пирамиды площадь основания вычисляется как произведение длины и ширины.
- Найдите высоту пирамиды. Это расстояние от вершины пирамиды до основания. Вы можете использовать геометрическую формулу или измерить это расстояние непосредственно.
- Найдите объем пирамиды, используя формулу V = (1/3) * S * h, где V - объем пирамиды, S - площадь основания, h - высота пирамиды.
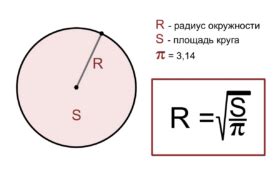
- Найдите радиус шара, вписанного в пирамиду, используя формулу r = (3V / 4π)^(1/3), где r - радиус шара, V - объем пирамиды, π - число пи.
Теперь у вас есть простое руководство по нахождению радиуса шара, вписанного в пирамиду! Просто следуйте этим шагам и вы сможете легко вычислить радиус.
Раздел 1: Определение понятия радиус
Радиус шара вписанного в пирамиду - это радиус шара, который полностью помещается внутри пирамиды, таким образом, что его центр совпадает с центром основания пирамиды, а его поверхность касается всех боковых граней пирамиды.
Измерение радиуса шара вписанного в пирамиду имеет большое значение при решении задач по геометрии и пространственному моделированию. Такой радиус позволяет определить геометрические свойства пирамиды и использовать их при проведении различных вычислений и конструировании трехмерных моделей.
Важно: Необходимо помнить, что радиус шара вписанного в пирамиду часто используется в теоретических расчетах и моделировании, и его значение может быть сложно определить на практике без специальных инструментов и измерительных приборов.
Раздел 2: Что такое пирамида и как она соотносится с шаром
Впишем шар в пирамиду. Рассмотрим случай, когда пирамида имеет квадратное основание. В этом случае шар будет касаться плоскостей, образуемых сторонами пирамиды, а его центр будет совпадать с центром квадрата. Радиус шара будет равен половине длины стороны квадрата.
| Описание | Формула |
|---|---|
| Радиус шара вписанного в пирамиду | Р = a/2 |
Где а - длина стороны квадрата, которое является основанием пирамиды.
Таким образом, радиус шара, вписанного в пирамиду с квадратным основанием, можно найти, используя формулу Р = a/2.
Раздел 3: Как найти высоту пирамиды

Высоту пирамиды можно найти, используя геометрические свойства фигуры и заданные параметры.
Существует несколько различных способов вычисления высоты пирамиды, в зависимости от известных данных. Рассмотрим каждый из них:
1. Если известны длина боковой стороны пирамиды и радиус вписанной окружности основания, можно воспользоваться формулой:
| h = (a^2 - r^2)^(1/2) |
где h - высота пирамиды, a - длина боковой стороны пирамиды, r - радиус вписанной окружности основания.
2. Если известны площадь основания пирамиды и ее объем, можно использовать следующую формулу:
| h = (3V)/(S) |
где h - высота пирамиды, V - объем пирамиды, S - площадь основания.
3. Если известны все боковые стороны пирамиды или ее ребра, можно воспользоваться формулой Герона:
| S = sqrt(p(p - a)(p - b)(p - c)) |
| h = 2S / a |
где S - площадь основания, a, b, c - длины боковых сторон или ребра пирамиды, p - полупериметр.
Выберите формулу, соответствующую известным данным, и подставьте значения, чтобы найти высоту пирамиды.
Раздел 4: Как найти площадь основания пирамиды
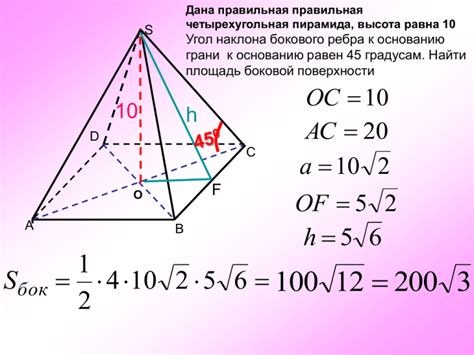
Если основание пирамиды является прямоугольником, площадь основания вычисляется по формуле: Площадь = длина * ширина.
Если основание пирамиды имеет форму круга, площадь основания вычисляется по формуле: Площадь = π * радиус^2, где π (пи) – математическая константа, примерное значение которой равно 3,14 и радиус – радиус круга.
Если основание пирамиды имеет форму другой геометрической фигуры, необходимо использовать соответствующую формулу для вычисления площади основания. Например, если основание представляет собой треугольник, площадь вычисляется по формуле Герона.
Важно помнить, что единицы измерения площади должны быть одинаковыми для всех величин, чтобы получить корректный результат. Например, если длина и ширина основания заданы в метрах, площадь будет выражена в квадратных метрах.
Зная площадь основания пирамиды, можно перейти к дальнейшим вычислениям, например, к нахождению радиуса шара, вписанного в данную пирамиду. Для этого потребуется использовать другие формулы и методы, которые будут рассмотрены в следующих разделах.
Раздел 5: Как найти образующую пирамиды
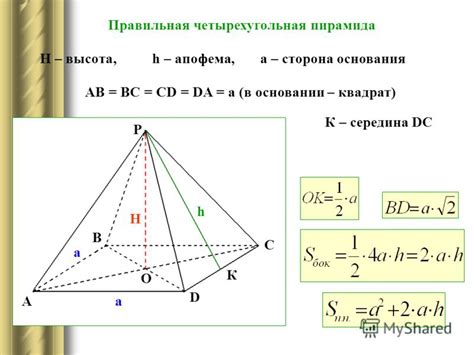
Для нахождения образующей пирамиды необходимо знать радиус основания пирамиды и высоту пирамиды. Поэтому, чтобы рассчитать длину образующей пирамиды, нужно сначала определить значение радиуса основания и высоту пирамиды.
Если радиус основания пирамиды уже известен, а высоту пирамиды необходимо найти, можно использовать соотношение между высотой пирамиды, радиусом основания и образующей пирамиды. Для этого может понадобиться применение треугольника, образованного высотой, образующей и радиусом основания.
Если неизвестна ни радиус основания пирамиды, ни высота пирамиды, необходимо использовать другие известные данные для определения длины образующей пирамиды. Возможно, понадобятся теоремы о пирамидах, использующих углы, длины сторон и другие характеристики пирамиды.
Поэтому, чтобы найти длину образующей пирамиды, необходимо анализировать имеющуюся информацию о пирамиде, использовать известные данные и применять соответствующие формулы и теоремы геометрии.
Раздел 6: Как найти объем пирамиды
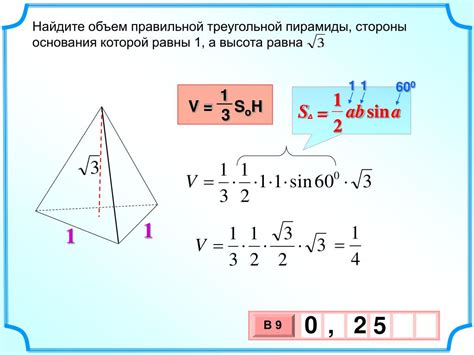
Чтобы найти объем пирамиды, нужно знать ее высоту и площадь основания. Объем пирамиды можно вычислить по формуле:
Объем = (площадь основания * высота) / 3
Для начала, измерьте площадь основания пирамиды. Если основание пирамиды является треугольником, используйте формулу для нахождения площади треугольника:
Площадь треугольника = (сторона a * сторона b * сторона c) / 4 * (полупериметр)
Если основание пирамиды является многоугольником, разделите его на более простые фигуры, для каждой из которых сможете найти площадь. Затем сложите площади этих фигур, чтобы получить общую площадь основания.
Когда вы найдете площадь основания и знаете высоту пирамиды, вставьте значения в формулу, чтобы найти объем пирамиды.
Убедитесь, что используете единицы измерения, согласованные с тем, в котором измерены площадь и высота пирамиды. Например, если площадь основания пирамиды измерена в квадратных сантиметрах, а высота в сантиметрах, объем будет выражаться в кубических сантиметрах.
Процесс нахождения объема пирамиды может немного усложниться, если пирамида имеет необычную форму или основание. В этом случае, возможно, потребуются дополнительные вычисления или цифры. Однако, если вы знаете площадь основания и высоту, основным шагом всегда будет использовать формулу объема пирамиды.
Раздел 7: Зависимость радиуса шара от площади основания и высоты пирамиды
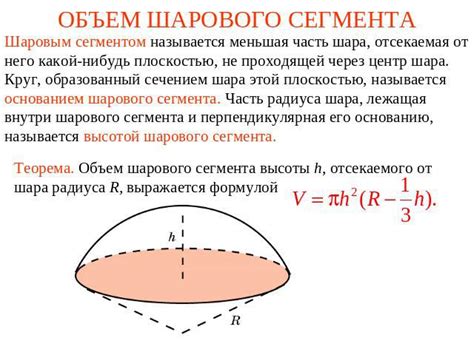
Для вычисления радиуса шара вписанного в пирамиду необходимо знать площадь основания и высоту пирамиды. В данном случае применяются следующие формулы:
- Радиус шара (r) может быть вычислен по формуле:
- r = √(S * h / (π * (1 + h2 / R2)))
- S - площадь основания пирамиды
- h - высота пирамиды
- R - радиус описанной окружности в основании пирамиды
- π - число "пи" (приближенное значение 3.14)
Используя данную формулу, можно легко и быстро вычислить радиус шара вписанного в пирамиду на основе известных значений площади основания и высоты пирамиды. Эта информация может быть полезна при проведении различных расчетов и построений в геометрии и строительстве.
Раздел 8: Пример расчета радиуса шара вписанного в пирамиду

Для расчета радиуса шара, вписанного в пирамиду, можно использовать следующий алгоритм:
- Найдите высоту пирамиды (h) и ее боковую сторону (a).
- Найдите площадь основания пирамиды (S) по формуле S = a^2.
- Вычислите объем пирамиды по формуле V = (1/3) * S * h.
- Вычислите радиус шара (R) по формуле R = (3V / 4π)^(1/3).
Давайте рассмотрим пример. Пусть высота пирамиды равна 5 единиц, а боковая сторона равна 4 единицы.
- Площадь основания пирамиды S = 4^2 = 16 единиц^2.
- Объем пирамиды V = (1/3) * 16 * 5 = 26.67 единиц^3.
- Радиус шара R = (3 * 26.67 / (4 * 3.14))^(1/3) = 2.38 единицы.
Таким образом, радиус шара вписанного в данную пирамиду равен 2.38 единицы.