Как правильно найти среднюю линию трапеции без лишних сложностей

Трапеция - это геометрическая фигура, которая имеет две параллельные стороны и две непараллельные стороны, известные как боковые стороны. Нахождение средней линии трапеции является важным шагом в решении геометрических задач, таких как вычисление площади или периметра трапеции.

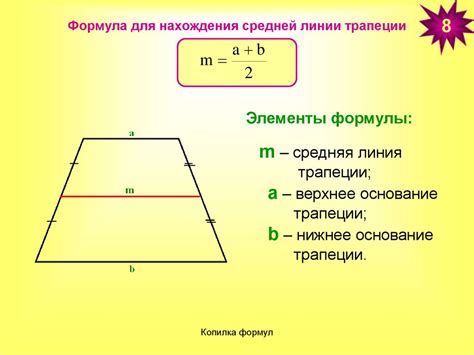
Средняя линия трапеции - это линия, которая соединяет середины двух непараллельных сторон трапеции. Это половина суммы этих сторон. Зная значения длин этих сторон, можно найти среднюю линию трапеции при помощи определенной формулы.

Для трапеции с параллельными сторонами a и b, а также высотой h, формула для нахождения средней линии m имеет следующий вид:

m = (a + b) / 2

На практике средняя линия трапеции может использоваться для вычисления площади этой фигуры. Если известны длина средней линии и высота, то можно воспользоваться следующей формулой:

S = m * h

Теперь, зная формулу и способ расчета средней линии трапеции, вы сможете легко решать задачи, связанные с этой геометрической фигурой и использовать полученные результаты в различных областях науки и техники.

Что такое трапеция и как ее найти?

Если известны длины оснований и высота трапеции, то можно найти ее площадь. Формула для нахождения площади трапеции выглядит следующим образом:

S = (a + b) * h / 2

Где S - площадь трапеции, a и b - длины оснований, h - высота трапеции.

Для нахождения средней линии трапеции нужно сложить длины оснований и поделить полученную сумму на 2. Формула для нахождения средней линии трапеции выглядит следующим образом:

M = (a + b) / 2

Где M - средняя линия трапеции, a и b - длины оснований.

Для удобства расчетов можно использовать таблицу, математический инструментарий или программное обеспечение, которые предлагают автоматические расчеты для трапеции.

Формула для нахождения средней линии трапеции

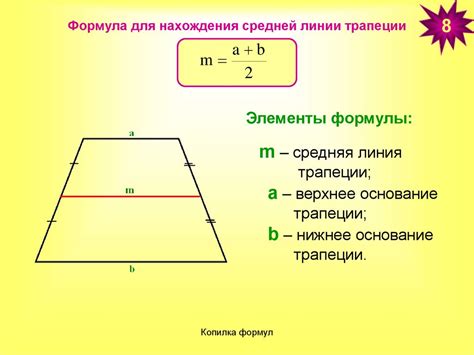
Формула для нахождения средней линии трапеции:

1. Найдите длины боковых сторон трапеции. Пусть a и b - длины оснований, c и d - длины боковых сторон.
2. Сложите длины боковых сторон и разделите полученную сумму на 2: (c + d) / 2.
3. Полученное значение будет являться длиной средней линии трапеции.

Например, пусть a = 5, b = 9, c = 4 и d = 6. Тогда:

1. Сумма длин боковых сторон: c + d = 4 + 6 = 10.
2. Деление суммы на 2: 10 / 2 = 5.

Таким образом, длина средней линии трапеции будет равна 5.

Используя данную формулу, вы сможете быстро и легко находить среднюю линию трапеции в любых задачах и расчетах.

Способы расчета средней линии трапеции

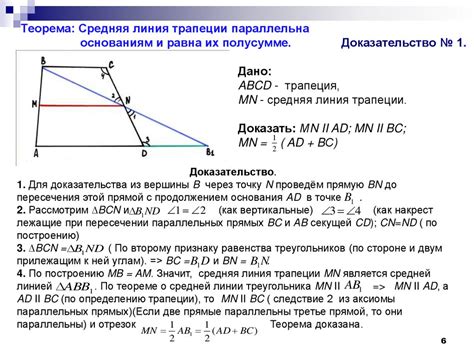
Существует несколько способов расчета средней линии трапеции:

1. Использование формулы: Средняя линия трапеции равна полусумме длин ее параллельных сторон. Математически это выглядит так: средняя_линия = (сторона_a + сторона_b) / 2.
2. Использование высоты: Средняя линия трапеции равна произведению высоты трапеции на полусумму длин ее параллельных сторон, разделенную на сумму длин этих сторон. Это может быть полезным, когда известна высота и длины сторон трапеции. Математически это выглядит так: средняя_линия = высота * (сторона_a + сторона_b) / (сторона_a + сторона_b).
3. Использование диагоналей: Если известны длины диагоналей трапеции, средняя линия может быть определена как среднее арифметическое длин диагоналей. Математически это выглядит так: средняя_линия = (диагональ_a + диагональ_b) / 2.
4. Использование площадей: Средняя линия трапеции может быть выражена через площадь трапеции и сумму длин ее базисов. Математически это выглядит так: средняя_линия = 2 * площадь_трапеции / (базис_a + базис_b).

Выбор метода расчета средней линии трапеции зависит от доступных данных и удобства использования определенной формулы. При проведении расчетов следует учесть, что значение средней линии трапеции является средним арифметическим значением длин параллельных сторон, и может быть использовано для дальнейших вычислений или анализа формы трапеции.

Примеры расчета средней линии трапеции

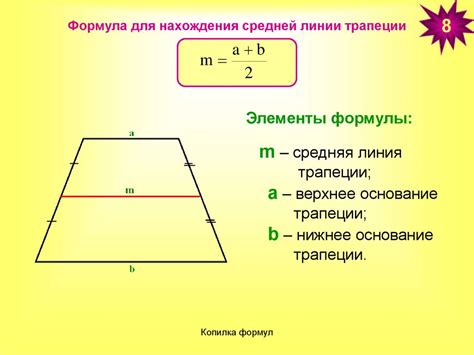
Для расчета средней линии трапеции необходимо знать длины оснований трапеции и высоту. Ниже приведены несколько примеров расчета этой величины.

Пример 1:

Дана трапеция со сторонами a = 5 см, b = 7 см и высотой h = 4 см.

С использованием формулы для средней линии трапеции: m = (a + b) / 2 = (5 + 7) / 2 = 12 / 2 = 6 см

Средняя линия данной трапеции равна 6 см.

Пример 2:

Дана трапеция со сторонами a = 10 см, b = 15 см и высотой h = 8 см.

С использованием формулы для средней линии трапеции: m = (a + b) / 2 = (10 + 15) / 2 = 25 / 2 = 12.5 см

Средняя линия данной трапеции равна 12.5 см.

Пример 3:

Дана трапеция со сторонами a = 3 см, b = 9 см и высотой h = 6 см.

С использованием формулы для средней линии трапеции: m = (a + b) / 2 = (3 + 9) / 2 = 12 / 2 = 6 см

Средняя линия данной трапеции равна 6 см.

Таким образом, средняя линия трапеции может быть вычислена с помощью простой формулы: m = (a + b) / 2, где a и b - длины оснований трапеции.

Значение средней линии трапеции в геометрии

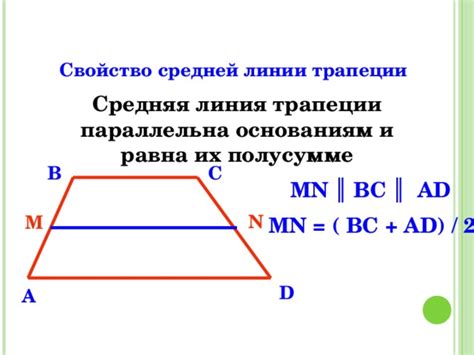
Для нахождения значения средней линии трапеции используется следующая формула:

Средняя линия = (основание 1 + основание 2) / 2

В данной формуле "основание 1" и "основание 2" представляют собой длины параллельных сторон трапеции.

Значение средней линии трапеции позволяет определить центральную ось симметрии фигуры. Она также является базисом для вычисления других характеристик трапеции, таких как площадь и периметр.

Полученное значение средней линии трапеции можно использовать при решении геометрических задач, например, для определения радиуса вписанной окружности или для нахождения высоты трапеции. Изучение средней линии трапеции помогает более полно понять и оценить данную фигуру и ее свойства.

Практическое применение средней линии трапеции

Средняя линия трапеции играет важную роль в различных областях исследования, инженерии и промышленности. Её расчет и применение позволяют решать множество задач, связанных с геометрией и механикой.

Одним из практических применений средней линии трапеции является определение площади трапеции. Зная длины оснований и высоту, можно легко найти среднюю линию трапеции с помощью формулы средней линии:

Знание средней линии трапеции может быть полезным при проектировании строений или изготовлении предметов с определенной геометрией, например, столов, столовых табличек или крышек. Она помогает определить геометрические параметры и подобрать подходящие размеры.

Кроме того, средняя линия трапеции может быть использована при расчете объема тела, образованного вращением трапеции вокруг оси. Это имеет практическое значение в теории механики, в сфере проектирования и моделирования различных машин и устройств.

Также, знание средней линии трапеции может быть полезным при решении задач на определение центра масс плоской фигуры, обладающей формой трапеции. Это помогает упростить расчеты и существенно ускоряет процесс анализа и исследования физических объектов.

В целом, средняя линия трапеции является важным инструментом в геометрии и механике, а её практическое применение позволяет решать различные задачи, связанные с геометрией, проектированием и анализом фигур и объектов.

Формула для расчета средней линии трапеции: средняя_линия = (сторона_1 + сторона_2) / 2.

Основные шаги для расчета средней линии трапеции:

1. Определить длины непараллельных сторон трапеции.
2. Применить формулу для расчета средней линии.
3. Выполнить вычисления.
4. Получить значение средней линии трапеции.

Важно помнить, что для расчета средней линии трапеции необходимо знать длины только непараллельных сторон, а также применять правильную формулу. Найти среднюю линию трапеции может быть полезным при решении геометрических задач или при работе с трапециями в реальных ситуациях.