Синус - одна из важнейших тригонометрических функций, широко используемая в физике для решения различных задач. Определение синуса основано на соотношении между длинами сторон прямоугольного треугольника и углом между ними. Важно уметь находить синус угла при решении задач в физике, чтобы эффективно применять его для расчетов и анализа физических процессов.
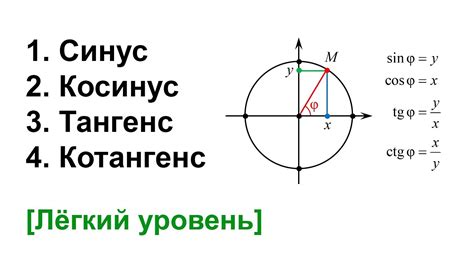
Синус угла φ в физике можно найти с помощью тригонометрических функций или таблицы значений. Основная формула для нахождения синуса угла φ гласит:
sin(φ) = противолежащая сторона/гипотенуза.
Также в физике существуют указания на значения синуса угла φ в таблицах или графиках, которые часто используются для упрощения вычислений. Такие таблицы и графики позволяют быстро определить значение синуса угла φ без необходимости проводить сложные расчеты. Но необходимо помнить, что подобные таблицы дают значения только для ограниченного диапазона углов и могут отличаться от истинных значений.
Зачем нужно знать синус φ в физике?
Знание синуса φ позволяет решать различные задачи, связанные с геометрией, механикой, электродинамикой и другими областями физики.
В геометрии, синус φ используется для вычисления длины противолежащего катета в прямоугольном треугольнике по известной гипотенузе и углу φ.
В механике, знание синуса φ позволяет определить силу, действующую на тело под углом φ к горизонтальной плоскости, при известной массе тела и его ускорении.
В электродинамике, синус φ используется для определения фазового сдвига между двумя взаимодействующими сигналами при изучении электрических колебаний и синхронных систем.
Также, знание синуса φ необходимо для понимания и расчета волновых явлений, оптики, звуковых колебаний и многих других явлений, связанных с физикой.
Установление законов физических явлений

Одним из примеров установления законов является закон Гука, который описывает связь между силой, действующей на упругое тело, и его деформацией. Для установления этого закона ученые проводят серию экспериментов, при которых измеряют силу, с которой тянут на упругое тело, и соответствующую деформацию. Анализируя полученные данные, ученые приходят к заключению, что сила, действующая на упругое тело, пропорциональна его деформации и обратно пропорциональна его упругой постоянной.
Еще одним примером установления законов является закон сохранения энергии. Для установления этого закона ученые проводят различные эксперименты, в которых измеряют начальную и конечную энергию системы. По результатам эксперимента ученые приходят к заключению, что энергия в системе сохраняется, то есть сумма начальной и конечной энергии остается неизменной.
Таким образом, установление законов физических явлений позволяет ученым описывать и объяснять различные физические процессы. Это является основой для развития физики как науки и применения ее результатов в различных областях жизни, включая технику, медицину, энергетику и другие.
Расчеты и прогнозирование результатов экспериментов

Для проведения расчетов синуса φ необходимо использовать соответствующие формулы. Одна из самых простых формул для расчета синуса φ имеет следующий вид:
| Угол (φ) | Синус (sin φ) |
|---|---|
| 0° | 0 |
| 30° | 0.5 |
| 45° | 0.707 |
| 60° | 0.866 |
| 90° | 1 |
Таблица представляет значения синуса φ для некоторых углов. Она может использоваться для оценки результатов эксперимента или для прогнозирования функциональных значений в тех случаях, когда точный расчет не требуется.
Однако, в реальных экспериментах синус фазового угла часто рассчитывается с использованием более сложных формул и учетом дополнительных переменных. Это позволяет получить более точные результаты и более полное представление о зависимости синуса φ от угла и других параметров эксперимента.
Расчеты и прогнозирование результатов экспериментов с использованием синуса φ являются неотъемлемой частью физических исследований. Точные и надежные расчеты позволяют получить новые знания о физических явлениях и разработать более эффективные методы и технологии в различных областях науки.
Применение синуса φ в различных областях физики
1. Механика:
Синус φ используется для расчета силы трения, когда объект движется по наклонной плоскости. Зная угол наклона плоскости и коэффициент трения, мы можем использовать формулу Fтрения = m * g * sin φ, где Fтрения - сила трения, m - масса объекта, g - ускорение свободного падения.
2. Акустика:
В акустике синус φ используется для описания колебаний звуковой волны. Амплитуда звуковой волны может быть представлена как A * sin(2πft + φ), где A - амплитуда, f - частота, t - время, φ - фаза колебаний.
3. Оптика:
Синус φ также применяется в оптике для расчета угла преломления света при переходе из одной среды в другую. Закон преломления Снеллиуса гласит, что n₁ * sin φ₁ = n₂ * sin φ₂, где n₁ и n₂ - показатели преломления сред, а φ₁ и φ₂ - углы падения и преломления соответственно.
4. Гидродинамика:
В гидродинамике синус φ используется для расчета силы сопротивления, действующей на тело, движущееся в жидкости. Формула силы сопротивления выглядит как Fсоп = 0.5 * ρ * v² * C * A * sin φ, где Fсоп - сила сопротивления, ρ - плотность жидкости, v - скорость тела, C - коэффициент сопротивления формы, A - площадь поперечного сечения тела.
| Область физики | Пример применения синуса φ |
|---|---|
| Механика | Расчет силы трения на наклонной плоскости |
| Акустика | Описание колебаний звуковой волны |
| Оптика | Расчет угла преломления света |
| Гидродинамика | Расчет силы сопротивления в жидкости |
Таким образом, синус φ играет важную роль в различных областях физики и позволяет решать широкий спектр задач.
Как определить значение синуса φ?

Одним из методов определения значения синуса φ является использование таблиц и графиков, где можно найти соответствующее значение синуса для заданного угла φ.
Также существуют специальные калькуляторы, которые позволяют найти значение синуса φ, вводя значение угла φ в градусах или радианах. Это наиболее точный и быстрый способ определения синуса φ.
Еще один способ определения значения синуса φ - использование тригонометрических формул и идентичностей. Например, формула синуса двойного угла: sin(2φ) = 2sin(φ)cos(φ).
Также можно использовать различные методы измерений, такие как использование тригонометрического круга или специальных устройств, чтобы определить значение угла φ и затем вычислить его синус.
И наконец, для некоторых особых значений угла φ, существуют простые геометрические и тригонометрические соотношения, которые позволяют сразу определить значение синуса φ. Например, sin(0°) = 0, sin(30°) = 0.5, sin(45°) = 1/√2 и т.д.
Важно помнить, что синус φ может быть выражен как функция угла в радианах или градусах. Поэтому при использовании формул и таблиц необходимо учитывать, в какой системе измерений задан угол φ.
Использование соответствующего метода определения значения синуса φ в каждом конкретном случае позволит точно решить задачи в физике, математике и других областях науки.
Угол, проекция и гипотенуза

Проекция угла φ на противоположную сторону называется противолежащей стороной, а проекция на прилежащую сторону - прилежащей стороной угла φ.
Для нахождения синуса φ воспользуйтесь следующей формулой:
sin(φ) = противолежащая сторона / гипотенуза
Таким образом, если известны значения противолежащей стороны и гипотенузы треугольника, можно легко вычислить синус угла φ при помощи данной формулы.
Применение тригонометрических таблиц и калькуляторов
Калькуляторы также представляют собой полезный инструмент для вычисления синуса различных углов. Современные научные калькуляторы обычно имеют функцию sin, которая автоматически вычисляет синус заданного угла. Для использования калькулятора требуется ввести значение угла в градусах или радианах и нажать соответствующую кнопку.
Какой инструмент выбрать - тригонометрическую таблицу или калькулятор - зависит от ситуации и предпочтений. Если нужно найти значение синуса для конкретного угла или набора углов, тригонометрическая таблица может быть наиболее удобной. Однако, если требуется найти значение синуса для произвольного угла или провести сложные вычисления, калькулятор может быть более эффективным и точным решением.
Формулы для вычисления синуса φ

В физике синус угла φ широко используется для вычисления различных физических величин. Вот некоторые из основных формул:
| Угол φ | Формула вычисления синуса φ |
|---|---|
| Прямоугольный треугольник | sin(φ) = противоположная сторона / гипотенуза |
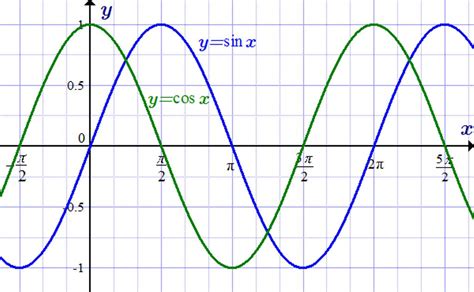
| Единичная окружность | sin(φ) = у-координата точки на окружности |
| Тригонометрические тождества | sin(φ) = cos(π/2 - φ) |
Эти формулы могут быть полезны при решении задач в физике, например, для вычисления силы, ускорения или траектории движения. Если вы знаете значение угла φ, то с помощью данных формул вы сможете найти его синус и использовать его для дальнейших расчетов. Удачи в изучении физики!