Сопротивление таблицам истинности может быть одной из самых сложных задач при изучении логики и математического моделирования. Составление таблицы истинности изначально требует точности и внимательности, чтобы избежать ошибок, которые могут привести к неправильным результатам.

Одним из основных методов поиска СДНФ (совершенной дизъюнктивной нормальной формы) таблицы истинности является использование Карт Карно. Карты Карно позволяют графически представить таблицу истинности в виде диаграммы. Для построения карты необходимо разделить все возможные комбинации значений переменных на прямоугольники.

После построения карты Карно необходимо найти прямоугольники, соответствующие каждому из максимальных конъюнктов в СДНФ. Для этого нужно определить, какие ячейки карты соответствуют 1 и вывести из них все возможные максимальные прямоугольники. Затем, используя максимальные прямоугольники, можно записать СДНФ таблицы истинности без ошибок.

Понятие СДНФ таблицы истинности

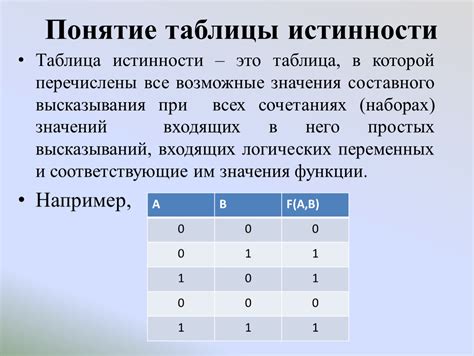
СДНФ позволяет выразить функцию в виде логического выражения, используя логические операции "ИЛИ" и "И". В СДНФ, каждому ряду таблицы истинности соответствует один макстерм, который содержит все переменные в соответствующих комбинациях значений переменных.

Таким образом, СДНФ представляет функцию как сумму произведений переменных или их отрицаний. Это позволяет легко определить значения функции для любых комбинаций значений переменных.

С использованием СДНФ можно строить минимальные конъюнкции, которые позволяют получить то же значение, что и исходная функция.

Найти СДНФ таблицы истинности без ошибок можно с помощью метода, основанного на анализе таблицы истинности и выделении макстермов.

Определение и основные принципы

Основными принципами поиска СДНФ таблицы истинности являются:

• Анализ таблицы истинности: необходимо провести анализ таблицы истинности для определения истинных и ложных значений функции при различных комбинациях входных переменных.
• Формирование конъюнкций: на основе анализа таблицы истинности формируются конъюнкции, составленные из переменных со значением 1 (истина) и их отрицаний со значением 0 (ложь).
• Дизъюнкция всех конъюнкций: полученные конъюнкции объединяются в дизъюнкцию, которая представляет собой СДНФ функции истинности.

Используя эти принципы, можно найти СДНФ таблицы истинности без ошибок и точно представить булеву функцию в виде дизъюнкции элементарных конъюнкций.

Зачем нужны СДНФ таблицы истинности

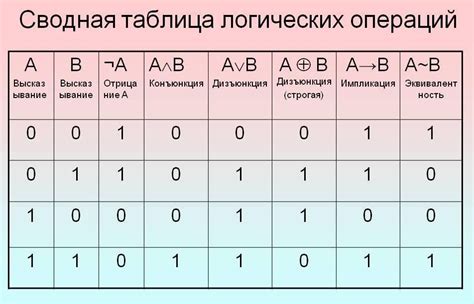
С помощью СДНФ таблицы истинности можно преобразовать таблицу истинности логического выражения в алгоритм, который может быть выполнен компьютером. Это позволяет сократить время и усилия, затрачиваемые на решение сложных задач, а также улучшить надежность и производительность программ.

Кроме того, СДНФ таблицы истинности позволяет наглядно представить и анализировать логические связи в системе или устройстве. Она позволяет выявлять ошибки в проектировании или программировании, а также оптимизировать работу системы или устройства.

Таким образом, СДНФ таблицы истинности являются мощным инструментом для анализа и проектирования логических систем. Они помогают выразить логическое выражение в алгоритмической форме, сократить время и усилия, затрачиваемые на решение задач, а также наглядно представить и анализировать логические связи.

Применение в логике и вычислительной технике

Система дизъюнктивных нормальных форм (СДНФ) нашла широкое применение в области логики и вычислительной техники. Она позволяет анализировать и описывать логические функции с помощью формул, состоящих из логических операций ИЛИ, И, НЕ и переменных. Такая форма представления позволяет удобным образом анализировать и программировать логические схемы и вычислительные алгоритмы.

Применение СДНФ в логике позволяет легко определять и анализировать истинности различных комбинаций переменных. С помощью таблиц истинности и применения правил логических операций можно точно определить результаты работы логической функции. Это особенно полезно при проектировании и проверке логических схем и алгоритмов, где требуется точное определение результатов исходя из заданных входных значений.

В вычислительной технике СДНФ активно применяется при проектировании и программировании цифровых устройств и алгоритмов. Она позволяет удобным образом описывать и анализировать логическое поведение различных устройств и алгоритмов. Например, при разработке компьютерных программ часто требуется определить правила для принятия решений в зависимости от разных значений входных данных. Использование СДНФ позволяет точно и лаконично задать эти правила и обеспечить корректную работу программы в различных ситуациях.

Как правильно составить СДНФ таблицы истинности без ошибок

Чтобы правильно составить СДНФ таблицы истинности без ошибок, необходимо выполнить следующие шаги:

Шаг 1: Составьте таблицу истинности для логической функции, определите все возможные значения переменных и значения функции при каждой комбинации переменных.

Шаг 2: Найдите строки таблицы истинности, в которых функция принимает значение "истина" (1).

Шаг 3: Для каждой строки, в которой функция равна "истине", составьте конъюнкцию (логическое "и") переменных, принимающих значение, соответствующее этой строке.

Шаг 4: Составьте совершенное дизъюнктивное выражение путем объединения полученных конъюнкций операцией дизъюнкции (логическое "или").

Шаг 5: Проверьте полученную формулу, подставив значения переменных из таблицы истинности и убедившись, что она соответствует значениям функции для всех комбинаций переменных.

Корректное составление СДНФ таблицы истинности без ошибок позволяет точно выразить логическую функцию и использовать ее для анализа и синтеза логических схем и систем.