Биквадратное уравнение – это уравнение вида ax4 + bx2 + c = 0, где a, b и c - заданные числа, а x - неизвестная переменная. Решение таких уравнений требует определенных навыков и техник, и, к счастью, существуют некоторые полезные советы, которые помогут вам в оформлении и решении биквадратных уравнений.
Первым шагом в решении биквадратного уравнения является оформление его в правильной форме. Проверьте, что все степени переменной корректны и что уравнение записано в общем виде. Если вам необходимо подготовить уравнение к решению, вы можете использовать методы замены переменных и факторизации, чтобы привести его к простой форме.
Пример:
Рассмотрим биквадратное уравнение: 5x4 - 12x2 + 3 = 0.
Для начала, убедитесь, что все степени переменной записаны в порядке убывания. В данном случае они уже упорядочены. Далее, можно применить замену переменных, чтобы сделать уравнение более подходящим для решения. Обозначим x2 = u. Тогда уравнение примет вид:
5u2 - 12u + 3 = 0.
Теперь можно решить полученное уравнение и найти значения переменной u. Затем, найдя значения u, можно вернуться к исходному уравнению и найти значения переменной x.
Следуя таким простым советам и правильно оформляя биквадратное уравнение, вы значительно упростите процесс его решения. Не бойтесь применять различные методы и техники, для достижения желаемого результата. Практика делает мастера, и с каждым разом вам будет все проще решать биквадратные уравнения.
Определение биквадратного уравнения

a2x4 + a1x2 + a0 = 0 |
где a2, a1, a0 – коэффициенты уравнения, причем a2 ≠ 0.
Для решения биквадратного уравнения необходимо найти значения переменной, при которых уравнение обращается в ноль. Решений может быть как два, так и четыре, в зависимости от значений коэффициентов и дискриминанта системы.
Понятие и структура биквадратного уравнения

Структура биквадратного уравнения выглядит следующим образом:
ax4 + bx2 + c = 0
Здесь:
- a, b и c – это коэффициенты, которые могут быть любыми числами, включая нуль;
- x – это переменная, которую нужно найти.
Следует отметить, что биквадратное уравнение всегда содержит два решения, так как уравнение четвертой степени имеет четыре решения. Кроме того, биквадратное уравнение может иметь одинаковые корни.
Для решения биквадратного уравнения можно воспользоваться различными методами, например, методом замены переменной, методом полного квадрата или методом факторизации.
Решение биквадратного уравнения может потребовать использования комплексных чисел, если дискриминант (значение под корнем в формуле решения уравнения) имеет отрицательное значение.
Также следует помнить о допустимых значениях переменной и исключать значения, при которых уравнение теряет смысл.
Решение биквадратного уравнения

Первый способ – использование замены переменной. Можно заменить исходное биквадратное уравнение другим уравнением, в котором степень уже равна двум. Затем решить это уравнение и подставить найденные значения назад. Этот способ может быть полезен, если исходное уравнение слишком сложно для прямого решения.
Второй способ – использование формулы для решения квадратного уравнения. Если в биквадратном уравнении коэффициент при старшей степени равен нулю, то его можно рассматривать как квадратное уравнение. В этом случае можно использовать известную формулу для нахождения корней квадратного уравнения.
Третий способ – использование факторизации. Если биквадратное уравнение можно факторизовать, то его можно решить путем выделения общего множителя и применения свойства нулевого произведения. Факторизация может потребовать некоторых алгебраических преобразований, но в некоторых случаях это может быть более удобным способом решения.
Решение биквадратного уравнения может потребовать некоторого времени и смекалки, но с практикой все сложности можно преодолеть. Применение разных способов решения позволяет найти оптимальное решение для каждого конкретного уравнения.
Методы решения биквадратного уравнения

a*x4 + b*x2 + c = 0
Решение биквадратного уравнения можно осуществить несколькими методами и приемами.
1. Замена переменной: чтобы убрать член со степенью 2, можно осуществить замену переменной. Например, если мы предполагаем, что t = x2, мы можем переписать биквадратное уравнение в виде:
a*t2 + b*t + c = 0
Полученное квадратное уравнение легче решить, так как для него существуют известные методы решения.
2. Квадратное уравнение: еще одним способом решения биквадратного уравнения является применение методов решения квадратных уравнений. Проводится замена переменной, чтобы привести биквадратное уравнение к квадратному виду. Например, если t = x2, то вместо исходного биквадратного уравнения мы решаем квадратное уравнение:
a*t2 + b*t + c = 0
3. Факторизация: некоторые биквадратные уравнения можно решить путем факторизации, то есть представления уравнения в виде произведения двух множителей. Затем решаются два квадратных уравнения вместо одного биквадратного. Например, для уравнения вида x4 - 16 = 0, мы можем провести факторизацию следующим образом:
| Выражение | Результат |
|---|---|
| (x2 - 4) * (x2 + 4) = 0 | Решаем два квадратных уравнения: |
| x2 - 4 = 0 | x = ±2 |
| x2 + 4 = 0 | Нет рациональных корней |
4. Корни квадратного уравнения: для частных случаев, когда биквадратное уравнение принимает форму квадратного уравнения, решение можно получить с помощью корней этого квадратного уравнения. Например, для уравнения x4 = 16, мы можем взять квадратный корень от обеих сторон, получив:
x2 = ±4
Затем извлекаем корни из квадратных уравнений:
x = ±2
Как видно из примеров, для решения биквадратных уравнений необходимо применять способы, основанные на заменах переменных, факторизации или методах решения квадратных уравнений. Выбор метода зависит от формы и условий задачи.
Применение дискриминанта при решении биквадратного уравнения

Дискриминант для биквадратного уравнения вычисляется по формуле: D = b^2 - 4ac, где a, b и c - коэффициенты уравнения.
Рассмотрим различные случаи, которые могут возникнуть при вычислении дискриминанта и их интерпретацию:
| Значение дискриминанта | Характеристика корней |
|---|---|
| D > 0 | Уравнение имеет два различных вещественных корня. |
| D = 0 | Уравнение имеет один вещественный корень. |
| D < 0 | Уравнение не имеет вещественных корней. |
Если уравнение имеет два различных вещественных корня, они могут быть найдены с помощью следующих формул:
x1 = (-b + √D) / (2a)
x2 = (-b - √D) / (2a)
Если уравнение имеет один вещественный корень, он может быть найден с помощью формулы:x = -b / (2a)
Если уравнение не имеет вещественных корней, это означает, что оно имеет комплексные корни.
Использование дискриминанта при решении биквадратного уравнения позволяет более точно определить его характеристики и найти значения корней. Этот инструмент является неотъемлемой частью алгоритма решения биквадратных уравнений и может быть полезным для упрощения решения.
Графическое представление биквадратного уравнения
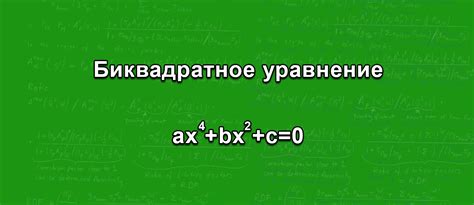
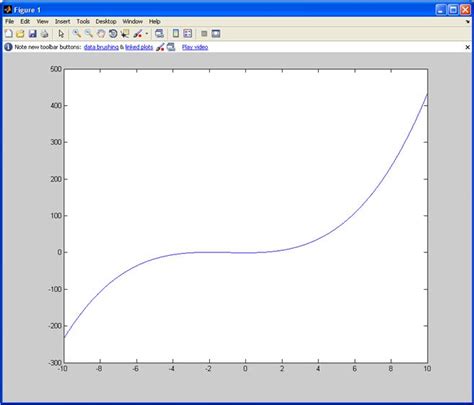
Для начала, необходимо построить график функции ax^4 + bx^2 + c на декартовой плоскости. Для этого достаточно выбрать несколько значений x, подставить их в функцию и построить соответствующие точки на графике.
Затем, соединяя эти точки гладкой кривой, можно получить график функции, который будет представлять собой кривую четвертого порядка.
Важно отметить, что график биквадратного уравнения может иметь различные формы в зависимости от значений коэффициентов a, b и c. Например, он может иметь форму параболы, или быть симметричным относительно оси Ox.
| Коэффициенты | График |
|---|---|
| a > 0, b = 0, c > 0 |  |
| a < 0, b = 0, c > 0 |  |
| a > 0, b = 0, c < 0 |  |
Таким образом, графическое представление биквадратного уравнения позволяет визуализировать его решения и увидеть, как изменяется график в зависимости от значений коэффициентов.
Построение графика биквадратного уравнения
- Определить ось симметрии. Если коэффициент при квадрате переменной по оси x равен нулю, то парабола будет параллельна оси y. В противном случае, она будет параллельна оси x.
- Найти вершину параболы. Вершина параболы может быть найдена по формуле
x = -\frac{b}{2a}, где a и b - коэффициенты уравнения. - Определить направление открытия параболы. Если коэффициент a положительный, парабола будет направлена вверх, иначе - вниз.
- Найти дополнительные точки. Для этого можно выбрать несколько значений переменной x и рассчитать соответствующие значения y по уравнению. Рекомендуется выбирать значения симметрично относительно вершины параболы.
- Построить график, используя полученные значения. Рекомендуется построить сетку, чтобы легче определить форму параболы и ее точки.
Важно помнить, что график биквадратного уравнения может иметь ноль, одну или две точки пересечения с осью x, а также различные формы в зависимости от значений коэффициентов. Построение графика позволяет визуально представить эти особенности уравнения.
Особенности графика биквадратного уравнения

График биквадратного уравнения представляет собой параболу с особыми особенностями, отличающимися от графика обычного квадратного уравнения. Рассмотрим основные особенности графика биквадратного уравнения:
- Симметрия относительно оси ординат: график биквадратного уравнения всегда симметричен относительно оси ординат. Это означает, что если точка (x, y) лежит на графике, то точка (-x, y) тоже лежит на графике.
- Ранее точек пересечения с осями координат: биквадратное уравнение может иметь одно, два или три решения. В зависимости от количества решений, график биквадратного уравнения может пересекать оси координат в одной, двух или трех точках.
- Нет экстремумов: в отличие от квадратного уравнения, биквадратное уравнение не имеет экстремумов. Это означает, что на графике биквадратного уравнения нет ни максимумов, ни минимумов.
- Изменение знака функции: основываясь на значениях коэффициента a в биквадратном уравнении, можно определить, в каких промежутках график функции находится выше или ниже оси абсцисс.
Изучив особенности графика биквадратного уравнения, вы сможете лучше понять его поведение и использовать это знание при решении задач и анализе функций.
Примеры решения биквадратных уравнений

Для решения биквадратного уравнения необходимо использовать специальную формулу, которая выражает корни уравнения через его коэффициенты. Рассмотрим несколько примеров, чтобы лучше понять процесс решения.
Пример 1:
Дано уравнение: x^4 - 4x^2 + 3 = 0
Решение:
Заметим, что данное уравнение является квадратным относительно переменной x^2. Поэтому мы можем ввести новую переменную y = x^2 и решить получившееся квадратное уравнение:
y^2 - 4y + 3 = 0
Далее, решим данное квадратное уравнение:
D = (-4)^2 - 4 * 1 * 3 = 16 - 12 = 4
y1 = (4 + √(4)) / 2 = (4 + 2) / 2 = 3
y2 = (4 - √(4)) / 2 = (4 - 2) / 2 = 1
Таким образом, получаем два значения для y: y1 = 3 и y2 = 1. Теперь найдем значения переменной x:
x1 = √(3) = ±√(3)
x2 = √(1) = ±1
Ответ: x1 = √(3), x2 = -√(3), x3 = 1, x4 = -1.
Пример 2:
Дано уравнение: 16x^4 - 36x^2 + 9 = 0
Решение:
Аналогично предыдущему примеру, данное уравнение является квадратным относительно переменной x^2. Вводим новую переменную y = x^2 и решаем:
y^2 - 36y + 9 = 0
Решим получившееся квадратное уравнение:
D = (-36)^2 - 4 * 1 * 9 = 1296 - 36 = 1260
y1 = (36 + √(1260)) / 2 = (36 + 2√(315)) / 2 = 18 + √(315)
y2 = (36 - √(1260)) / 2 = (36 - 2√(315)) / 2 = 18 - √(315)
Таким образом, получаем два значения для y: y1 = 18 + √(315) и y2 = 18 - √(315). Затем находим значения переменной x:
x1 = √(18 + √(315))
x2 = -√(18 + √(315))
x3 = √(18 - √(315))
x4 = -√(18 - √(315))
Ответ: x1 ≈ 1.655, x2 ≈ -1.655, x3 ≈ 0.195, x4 ≈ -0.195.
Примеры выше показывают, как использовать формулу для решения биквадратных уравнений. Помните, что значения корней будут комлексными, если дискриминант отрицательный.
Примеры решения биквадратных уравнений с положительными корнями

Рассмотрим несколько примеров:
Пример 1:
Решим уравнение: 4x^4 - 9 = 0.
Находим корни биквадратного уравнения:
x^2 = ±√(9/4) = ±3/2.
Проверяем, являются ли найденные корни положительными:
x^2 = 3/2 > 0, следовательно x ≠ -3/2, +3/2.
Поскольку найденные значения не являются положительными, уравнение не имеет положительных корней.
Пример 2:
Решим уравнение: 2x^4 - 8 = 0.
Находим корни биквадратного уравнения:
x^2 = ±√(8/2) = ±2.
Проверяем, являются ли найденные корни положительными:
x^2 = 2 > 0, следовательно x ≠ -2, +2.
Поскольку найденные значения не являются положительными, уравнение не имеет положительных корней.
Пример 3:
Решим уравнение: x^4 - 7 = 0.
Находим корни биквадратного уравнения:
x^2 = ±√(7/1) = ±√7.
Проверяем, являются ли найденные корни положительными:
x^2 = √7 > 0, следовательно x ≠ -√7, +√7.
Поскольку найденные значения не являются положительными, уравнение не имеет положительных корней.
Таким образом, когда корни биквадратного уравнения не являются положительными числами, уравнение не имеет положительных корней.
Примеры решения биквадратных уравнений с отрицательными корнями

Решение биквадратных уравнений может быть интересным и разнообразным. Рассмотрим примеры решения биквадратных уравнений, в которых получаем отрицательные корни.
Пример 1:
Рассмотрим уравнение x^4 + 6x^2 + 9 = 0. Для начала заметим, что это уравнение является биквадратным, так как степень переменной x равна 4. Приведем его к квадратному виду, представив переменную x^2 как новую переменную y:
y^2 + 6y + 9 = 0
Теперь решим полученное квадратное уравнение с помощью дискриминанта:
D = b^2 - 4ac = 6^2 - 4 * 1 * 9 = 36 - 36 = 0
Так как дискриминант равен нулю, получаем один корень:
y = -b / (2a) = -6 / (2 * 1) = -6 / 2 = -3
Теперь найдем значения переменной x с помощью обратной замены переменной:
x^2 = -3
Так как мы рассматриваем только действительные корни, отрицательный корень будет иметь вид:
x = √(-3) = √(-1 * 3) = √(-1) * √(3) = i√3
Итак, получаем два значения переменной x:
x = i√3
x = -i√3
Пример 2:
Рассмотрим уравнение 9x^4 - 36x^2 + 36 = 0. Приведем его к квадратному виду, представив переменную x^2 как новую переменную y:
9y^2 - 36y + 36 = 0
Решим полученное квадратное уравнение с помощью дискриминанта:
D = b^2 - 4ac = (-36)^2 - 4 * 9 * 36 = 1296 - 1296 = 0
Дискриминант равен нулю, следовательно, уравнение имеет один корень:
y = -b / (2a) = 36 / (2 * 9) = 36 / 18 = 2
Используя обратную замену переменной, найдем значения переменной x:
x^2 = 2
Так как мы рассматриваем только действительные корни, отрицательный корень будет иметь вид:
x = √2
Итак, получаем два значения переменной x:
x = √2
x = -√2
Таким образом, мы рассмотрели примеры решения биквадратных уравнений с отрицательными корнями. Используя подход к приведению уравнений к квадратному виду и решение полученных квадратных уравнений, мы смогли найти значения переменных, удовлетворяющие исходным уравнениям.