Четверть окружности - это одна из четырех равных частей, на которые делится окружность. Каждая из них имеет свои особенности и значения углов. Определение четверти окружности является важным знанием в геометрии и может быть полезным при решении различных задач и проблем.
Существует несколько алгоритмов и способов определения четверти окружности, в зависимости от предоставленных данных и условий задачи. Один из наиболее распространенных методов - это определение положения точки на плоскости относительно центра окружности.
Пусть дана окружность с центром в точке O(x0,y0) и радиусом R. Для определения четверти точки P(x,y), необходимо проанализировать знаки координат х и у.
Если х > х0 и у > у0, то точка P находится в первой четверти окружности. Если х < х0 и у > у0, то точка P находится во второй четверти окружности. Если х < х0 и у < у0, то точка P находится в третьей четверти окружности. А если х > х0 и у < у0, то точка P находится в четвертой четверти окружности.
Таким образом, зная координаты центра окружности и координаты точки, мы можем определить четверть окружности, в которой находится эта точка.
Определение четверти окружности
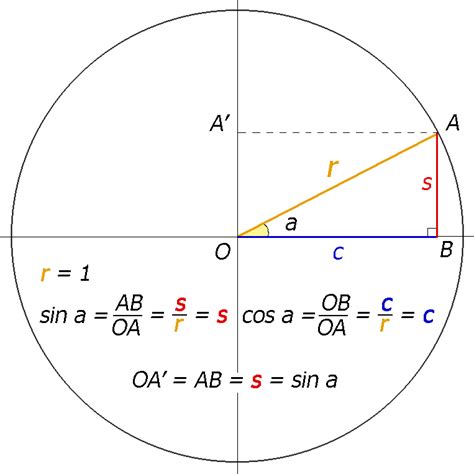
Окружность состоит из 4 четвертей, которые определяются в зависимости от положения точки на плоскости относительно центра окружности.
Чтобы определить четверть окружности, необходимо знать координаты точки-координаты (x,y) и центра окружности (h,k). Важно помнить, что положительные x находятся вправо от центра, а положительные y - вверх.
Ниже представлены алгоритмы и способы определения четверти окружности:
- Если x > h и y > k, то точка находится в первой четверти.
- Если x < h и y > k, то точка находится во второй четверти.
- Если x < h и y < k, то точка находится в третьей четверти.
- Если x > h и y < k, то точка находится в четвёртой четверти.
Зная координаты точки и центра окружности, вы можете легко определить четверть окружности, в которой она находится.
Это может быть полезно при решении задач в геометрии, программировании или в других областях, требующих работы с окружностями и их четвертями.
Использование координат точек

Для определения четверти окружности необходимо проанализировать положение точки относительно центра окружности:
| Четверть | Условие |
|---|---|
| I | x > Cx и y > Cy |
| II | x < Cx и y > Cy |
| III | x < Cx и y < Cy |
| IV | x > Cx и y < Cy |
На основе этих условий можно реализовать алгоритм, который будет определять четверть окружности по заданным координатам.
Расчет по значениям угла
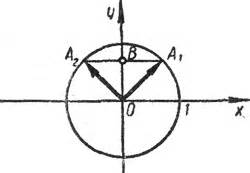
Круг состоит из 360 градусов. Для определения четверти окружности по значению угла можно использовать следующие соотношения:
- Если угол находится в диапазоне от 0 до 90 градусов, то точка находится в первой четверти окружности.
- Если угол находится в диапазоне от 90 до 180 градусов, то точка находится во второй четверти окружности.
- Если угол находится в диапазоне от 180 до 270 градусов, то точка находится в третьей четверти окружности.
- Если угол находится в диапазоне от 270 до 360 градусов, то точка находится в четвертой четверти окружности.
Для определения четверти окружности достаточно знать значение угла и сравнить его с указанными диапазонами.
Ориентация вектора

Тема ориентации вектора имеет важное значение при определении четверти окружности. Ориентация вектора может быть положительной или отрицательной, в зависимости от направления вектора и оси координат.
Ориентация положительна, если вектор поворачивается против часовой стрелки относительно положительной оси x. В этом случае вектор находится в верхней или правой полуплоскости.
Ориентация отрицательна, если вектор поворачивается по часовой стрелке относительно положительной оси x. В этом случае вектор находится в нижней или левой полуплоскости.
Для определения ориентации вектора можно использовать различные алгоритмы, включая вычисление косинуса угла между вектором и осью, определение знака произведения координат или использование геометрических свойств окружности. Точный алгоритм выбирается в зависимости от конкретной задачи и необходимой точности.
| Ориентация | Направление вектора | Полуплоскость |
|---|---|---|
| Положительная | Против часовой стрелки | Верхняя или правая |
| Отрицательная | По часовой стрелке | Нижняя или левая |
Правильно определенная ориентация вектора поможет определить положение точки относительно окружности и, следовательно, выбрать правильную четверть окружности.
Верификация результатов

После применения алгоритмов и способов определения четверти окружности, необходимо проверить полученные результаты на достоверность. Верификация позволяет убедиться, что ответы правильные и соответствуют ожидаемым значениям. В данном контексте этот этап имеет особое значение, так как верное определение четвертей окружности может быть критически важным для решения множества задач и проблем.
Для верификации результатов можно использовать различные методики, зависящие от того, какой алгоритм был применен для определения четверти окружности. Например, если использовался графический метод, то можно визуально сравнить полученные результаты с изображением окружности и убедиться в их совпадении.
Другим способом верификации может быть математическое сравнение полученных значений с ожидаемыми. Если алгоритм был реализован на основе формул, то можно сравнить полученный результат с результатом, полученным вручную с помощью этих же формул.
Также, на этапе верификации результатов следует обратить внимание на возможные ошибки округления, вычислительные погрешности и другие факторы, которые могут повлиять на точность полученных значений. В таких случаях стоит использовать специальные методы анализа ошибок и корректировать результаты соответствующим образом.
Верификация результатов является важным этапом при определении четверти окружности. Она позволяет проверить полученные ответы на правильность и убедиться в их достоверности. Правильная верификация гарантирует корректность решения задач и позволяет избежать возможных ошибок при использовании результатов в дальнейшей работе.