Напряжение в смешанном соединении резисторов является одной из фундаментальных характеристик электрической цепи. Правильное определение этого значения позволяет рассчитать ток и мощность, а также эффективно проектировать и отлаживать электрические схемы.
Для расчета напряжения в смешанном соединении резисторов необходимо знать значения сопротивления каждого резистора в цепи и значения токов, протекающих через каждый из них. Существует несколько методов для определения напряжения в таком соединении, и мы рассмотрим их один за другим, приведя примеры и пояснения к каждому из них.
Один из самых простых способов – применение закона Ома. Согласно этому закону, напряжение пропорционально силе тока и сопротивлению в цепи. Таким образом, для нахождения напряжения достаточно перемножить ток на сопротивление конкретного резистора. Примерные расчеты позволят лучше разобраться в этом методе и его применении.
Пример:
Если в смешанной цепи имеется два резистора со значениями 5 Ом и 10 Ом, а ток в цепи составляет 2 А, то для определения напряжения на каждом из резисторов можно использовать следующую формулу:
U = I * R
Подставив вместо I значение 2 А, а вместо R – 5 Ом (U1 = 2 * 5 = 10 В) и 10 Ом (U2 = 2 * 10 = 20 В), мы получим напряжения на каждом из резисторов в смешанной цепи. Таким образом, напряжение в смешанном соединении резисторов может быть определено с помощью простых математических расчетов.
Что такое смешанное соединение резисторов?
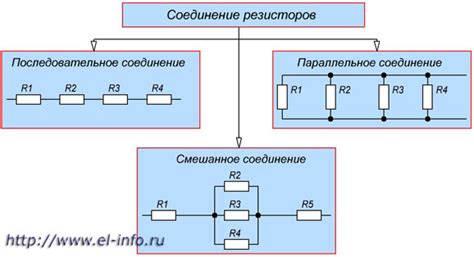
Смешанное соединение резисторов представляет собой комбинацию различных типов соединений резисторов, таких как последовательное и параллельное. В таком соединении присутствуют как резисторы, соединенные последовательно, так и резисторы, которые параллельно соединены друг с другом. Смешанное соединение резисторов может быть использовано для создания сложных цепей с нужными электрическими характеристиками.
В смешанном соединении резисторов каждый резистор может влиять на общее сопротивление цепи и ее характеристики. Для нахождения общего сопротивления цепи в смешанном соединении применяются соответствующие формулы и правила, которые позволяют провести расчеты и определить, как изменится напряжение при подключении внешнего источника энергии.
Смешанное соединение резисторов может использоваться, например, в электрических схемах, где требуется создание разного уровня сопротивления для различных участков цепи. Такое соединение позволяет настраивать и контролировать электрические параметры цепи, обеспечивая требуемые электрические характеристики.
Какие методы можно использовать для нахождения напряжения в смешанном соединении резисторов?
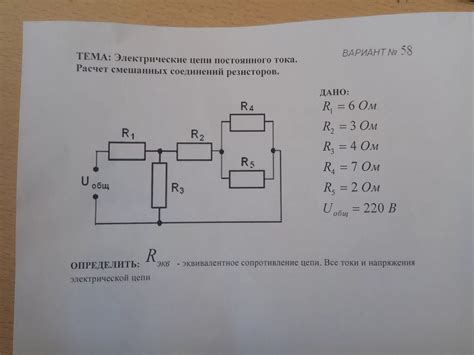
Для определения напряжения в смешанном соединении резисторов можно использовать различные методы, в зависимости от известных данных и условий задачи. Рассмотрим несколько распространенных подходов:
Метод деления напряжения
Этот метод основывается на законе Кирхгофа о сумме напряжений в замкнутом контуре. При соединении резисторов в цепи можно использовать этот закон, чтобы найти напряжение на каждом из них. Для этого необходимо знать общее напряжение и сопротивления каждого резистора. Выразив соотношение между известными и неизвестным напряжениями с помощью деления, можно получить искомое значение.
Метод замены резисторов
Этот метод основывается на замене смешанного соединения резисторов на замененный эквивалентный резистор. Для этого необходимо провести анализ цепи и определить, какие резисторы можно объединить в параллель или последовательность. Затем можно заменить группы резисторов на эквивалентные им резисторы и использовать известные формулы для расчета напряжения в новой упрощенной цепи.
Метод сочетания двух методов
В некоторых случаях можно использовать комбинацию методов деления напряжения и замены резисторов. Например, можно применить метод деления напряжения для определения значения напряжения на одном из резисторов, а затем использовать метод замены резисторов для упрощения и вычисления напряжения в оставшейся части цепи.
Важно помнить, что для применения этих методов необходимо знать значения сопротивлений каждого резистора и иметь информацию об общем напряжении в цепи. Также стоит учитывать, что в реальных схемах могут присутствовать дополнительные факторы, такие как внутреннее сопротивление источника питания, которые могут влиять на расчет напряжения.
Метод замещения: определение и применение

Для применения метода замещения необходимо знать значения сопротивлений всех резисторов в смешанном соединении. Затем нужно выделить интересующую нас часть цепи и заменить ее эквивалентным резистором. Этот эквивалентный резистор имеет такое же сопротивление, как и исходная часть цепи, но представлен в виде одного простого элемента.
После замены резисторов эквивалентными значениями, можно использовать более простую схему для решения задачи. Например, если задача находится в напряжении на одном из резисторов, то после замены можно использовать законы Кирхгофа и закон Ома для определения напряжения на эквивалентном резисторе.
Применение метода замещения значительно упрощает решение задач, связанных с смешанными соединениями резисторов. Оно позволяет сократить количество элементов цепи и провести анализ с использованием известных законов электрических цепей.
Пример:
Допустим, у нас есть схема смешанного соединения резисторов, в которой присутствуют резисторы R1, R2 и R3. Чтобы использовать метод замещения, мы выделяем часть цепи, включающей резисторы R2 и R3, и заменяем эту часть эквивалентным резистором R23.
После замены резисторов R2 и R3 эквивалентным резистором R23, мы получаем более простую схему, в которой оставшиеся резисторы соединены последовательно. Теперь мы можем использовать законы электрических цепей для определения напряжения на резисторе R23 или на любом другом резисторе в схеме.
Таким образом, метод замещения позволяет упростить решение сложных электрических цепей, смешанных соединений резисторов. Он является мощным инструментом в расчетах и анализе электрических схем.
Пример использования метода замещения для нахождения напряжения

Рассмотрим следующую ситуацию: имеется смешанное соединение с двумя параллельными резисторами - R1 и R2, а также последовательно подключенным к ним резистором R3. Необходимо найти напряжение на резисторе R3.
Для начала применим метод замещения для параллельных резисторов R1 и R2. Заменим их эквивалентным резистором Rp сопротивлением Rp = 1 / (1 / R1 + 1 / R2).
Теперь получившуюся схему можно упростить: резистор Rp параллельно подключен к резистору R3. Это означает, что напряжение на резисторе Rp также будет напряжением на резисторе R3.
Таким образом, чтобы найти напряжение на резисторе R3, достаточно найти напряжение на эквивалентном резисторе Rp. Для этого можно использовать любой известный метод определения напряжения, например, закон Ома.
Таким образом, применение метода замещения позволяет существенно упростить сложные смешанные соединения и легче находить напряжения на отдельных резисторах.
Метод комплексных амплитуд: что это и как применять

Для применения метода комплексных амплитуд вам необходимо знать значения сопротивлений каждого резистора в цепи и частоту переменного тока, применяемого в цепи.
Для начала вам необходимо преобразовать каждое сопротивление резистора в комплекснозначное сопротивление, используя формулу: Z = R + jωL, где Z - комплексное сопротивление, R - сопротивление резистора, j - мнимая единица, ω - угловая частота переменного тока, L - индуктивность резистора.
Затем вычислите общее комплексное сопротивление цепи, суммируя все комплексные сопротивления резисторов с помощью алгебраической операции сложения. Полученное значение обозначим как Zобщ.
Напряжение в смешанном соединении резисторов можно определить с помощью формулы: U = I * Zобщ, где U - напряжение, I - сила тока.
Зная значение напряжения, вы можете использовать его для решения других электрических задач, например, для вычисления тока в цепи или мощности резисторов.
Метод комплексных амплитуд является эффективным инструментом для анализа смешанных соединений резисторов, поскольку он позволяет учесть как активное, так и реактивное сопротивление цепи. Он также является основой для более сложных методов анализа цепей, таких как метод узловых потенциалов или метод контурных токов.
Теперь вы знаете, что такое метод комплексных амплитуд и как его применять для определения напряжения в смешанном соединении резисторов. Используйте этот метод, чтобы более точно анализировать и решать электрические задачи.
Пример использования метода комплексных амплитуд для нахождения напряжения

Для наглядности рассмотрим пример: имеется смешанное соединение из двух резисторов R1 и R2, подключенных к источнику переменного напряжения с амплитудой V0 и частотой f. Необходимо найти напряжение на резисторе R2.
Шаг 1: Преобразование резисторов в комплексные импедансы. Для этого используем формулу Z = R + jX, где R - активное сопротивление (реальная часть импеданса), X - реактивное сопротивление (мнимая часть импеданса). Для резисторов X = 0.
- R1 = 10 Ом, X1 = 0;
- R2 = 20 Ом, X2 = 0.
Шаг 2: Суммирование импедансов резисторов. Для смешанного соединения, импеданс можно найти как сумму импедансов отдельных элементов.
Z_total = Z1 + Z2 = (R1 + jX1) + (R2 + jX2).
- При подстановке значений из шага 1 получаем: Z_total = (10 + j0) + (20 + j0) = 30 + j0 Ом.
Шаг 3: Расчет тока через смешанное соединение. Для этого используем закон Ома: I = V / Z_total, где V - амплитуда напряжения источника переменного тока.
- Пусть V = V0 * exp(jωt), где ω = 2πf. Тогда I = (V0 * exp(jωt)) / (30 + j0).
Шаг 4: Нахождение напряжения на резисторе R2. Для этого используем закон Ома: U = I * Z2, где U - амплитуда напряжения на резисторе R2.
- Исходя из шага 3, можно записать: U = I * (R2 + jX2) = ((V0 * exp(jωt)) / (30 + j0)) * (20 + j0).
- Выполнив необходимые алгебраические преобразования, получим: U = (2/3)V0 * exp(jωt).
Итак, мы получили выражение для напряжения на резисторе R2 в смешанном соединении:
U = (2/3)V0 * exp(jωt).
Этот пример демонстрирует, как метод комплексных амплитуд может быть использован для нахождения напряжения на отдельных элементах смешанного соединения резисторов. Применение комплексной алгебры и импедансов позволяет упростить расчеты и получить точные результаты.
Как выбрать наиболее подходящий метод для нахождения напряжения в смешанном соединении резисторов?

Нахождение напряжения в смешанном соединении резисторов может быть вызовом, но существует несколько методов, которые могут помочь вам успешно решить эту задачу. Какой метод выбрать? Это зависит от конкретной ситуации и от вашего уровня знаний в области электричества.
Один из самых простых методов - это использование закона Ома. Согласно этому закону, разность потенциалов между двумя точками на цепи равна произведению силы тока на сумму сопротивлений на пути этого тока. Если вам известны значения сопротивлений и сила тока, вы можете легко вычислить напряжение.
Если смешанное соединение резисторов содержит параллельные ветви, то можно воспользоваться правилом сопротивлений при последовательном соединении. Согласно этому правилу, общее сопротивление цепи равно сумме сопротивлений в параллельных ветвях. Затем можно использовать закон Ома для нахождения напряжения.
Если вы ищете более сложный метод для нахождения напряжения в смешанном соединении резисторов, вы можете использовать метод узловых потенциалов или метод контурных токов. Эти методы основаны на применении систем уравнений с учетом законов Кирхгофа.
Все эти методы имеют свои преимущества и ограничения. При выборе метода учитывайте его сложность, доступность необходимой информации и ваши личные навыки в решении подобных задач. Практика и опыт помогут вам выбрать наиболее подходящий метод для решения конкретной задачи.