Треугольник – одна из самых основных и изучаемых геометрических фигур. Большинство задач, связанных с треугольниками, требуют знания нескольких параметров, включая основание и высоту. Часто случается, что основание треугольника неизвестно, но известна только его высота. В данной статье мы рассмотрим, как определить основание треугольника по заданной высоте.
Основа треугольника – это одна из его сторон, которая лежит на линии, перпендикулярной к высоте. Основание служит началом и концом отсчета длины всех других сторон треугольника. Определить основание треугольника по высоте можно с помощью простой формулы, которую мы рассмотрим далее.
Существует несколько способов определения основы треугольника по его высоте. Во-первых, можно воспользоваться формулой, которая связывает площадь треугольника с длиной его высоты и основания. Формула имеет вид:
Площадь = (Основание * Высота) / 2.
Используя эту формулу, можно выразить основание треугольника:
Основание = (Площадь * 2) / Высота.
Что такое треугольник и его основание?

Основание может быть любой из сторон треугольника, и его выбор зависит от контекста задачи или геометрической фигуры, с которой мы работаем. Обычно основание обозначается буквой "a", "b" или "c", что соответствует сторонам треугольника.
Высота треугольника - это отрезок, проведенный из вершины треугольника до основания под прямым углом. Высота может быть опущена из любой из вершин треугольника.
Определение основания треугольника по высоте важно при решении различных задач из геометрии и использовании формул для вычисления площади треугольника или других его характеристик.
Важно помнить, что основание треугольника и его высота взаимосвязаны, и знание одной из этих величин позволяет нам рассчитать другую.
Зачем нужно определить основание треугольника по высоте?

Одной из наиболее распространенных ситуаций, когда необходимо определить основание треугольника по его высоте, является нахождение площади этой фигуры. Для этого используется формула: площадь треугольника равна произведению половины основания на высоту треугольника. Таким образом, зная высоту и площадь треугольника, можно выразить основание и узнать его значение.
Определение основания треугольника по высоте также полезно при решении задач на подобие и сходство треугольников. Подобные треугольники имеют пропорциональные стороны, а значит, если известны высоты и одна сторона треугольника, можно найти соответствующие стороны другого треугольника.
Кроме того, зная высоту и основание треугольника, можно провести различные геометрические построения и доказательства, например, найти обратную стрелку, которая соединяет вершину треугольника с серединой основания и перпендикулярна его основанию.
Определение основания треугольника по его высоте имеет широкое применение в геометрии и математике. Это важный инструмент, позволяющий решать различные задачи, находить неизвестные параметры треугольников и проводить геометрические построения.
Как найти основание треугольника по высоте?

Определить основание треугольника по известной высоте может быть полезным для решения различных геометрических задач. Следуя нескольким простым шагам, вы сможете точно найти значение основания треугольника.
1. Вспомните базовую формулу для площади треугольника: S = (b * h) / 2, где S - площадь, b - основание, h - высота.
2. Если вы знаете площадь и высоту треугольника, подставьте значения в формулу и выразите основание: b = (2 * S) / h.
3. Если вы знаете только высоту и одну сторону треугольника, воспользуйтесь формулой для площади: S = (b * h) / 2, где b - основание, h - высота. Выразите основание: b = (2 * S) / h.
4. Если вы знаете только высоту и угол, воспользуйтесь формулой для площади: S = (b * h) / 2, где b - основание, h - высота. Выразите основание: b = (2 * S) / h.
5. Если вы знаете длину двух сторон и угол между ними, примените формулу для площади треугольника: S = (b * h) / 2, где b - основание, h - высота. Выразите основание: b = (2 * S) / h.
6. В некоторых случаях вы можете использовать теорему Пифагора или тригонометрию для нахождения основания треугольника.
Итак, зная высоту и другую информацию о треугольнике, вы сможете без труда определить значение его основания. Удачных вам вычислений!
Метод 1: Формула высоты и площади

Один из способов определения основания треугольника по высоте заключается в использовании формулы высоты и площади. Для этого необходимо знать значение высоты и площади треугольника.
Высота треугольника – это отрезок, проведенный из вершины треугольника до противоположной стороны и перпендикулярный этой стороне. Площадь треугольника может быть найдена, например, по формуле "площадь = 0,5 * основание * высота".
Для определения основания треугольника по высоте воспользуемся этой формулой. Для этого необходимо знать значение высоты и площади треугольника. Подставив эти значения в формулу, можно выразить основание как "основание = (2 * площадь) / высота".
Например, пусть задан треугольник с высотой, равной 6 и площадью, равной 18. Установим значения в формулу и вычислим основание следующим образом: основание = (2 * 18) / 6 = 6.
Таким образом, основание треугольника, при условии заданных высоты и площади, равно 6.
Метод 2: Использование теоремы Пифагора
Предположим, что у нас есть треугольник ABC, где AB - высота, BC - гипотенуза, а AC - основание треугольника.
1. Измерьте длину высоты AB и гипотенузы BC.
2. Возведите длину высоты AB в квадрат и обозначьте эту величину как AB^2.
3. Возведите длину гипотенузы BC в квадрат и обозначьте эту величину как BC^2.
4. Вычислите величину AC^2, используя теорему Пифагора: AC^2 = BC^2 - AB^2.
5. Извлеките квадратный корень из значения AC^2, чтобы найти длину основания AC.
Пример:
Предположим, что у нас есть треугольник ABC, где AB = 6 и BC = 10. Мы хотим найти длину основания AC.
1. AB^2 = 6^2 = 36
2. BC^2 = 10^2 = 100
3. AC^2 = 100 - 36 = 64
4. AC = √64 = 8
Таким образом, длина основания треугольника AC равна 8.
Примеры нахождения основания треугольника по высоте
Для определения основания треугольника по заданной высоте необходимо использовать соответствующие формулы. Рассмотрим несколько примеров:
| Пример | Высота | Основание |
|---|---|---|
| Пример 1 | 6 см | 12 см |
| Пример 2 | 8 см | 16 см |
| Пример 3 | 10 см | 20 см |
Для решения этих примеров мы использовали формулу площади треугольника:
S = 1/2 * a * h,
где S - площадь треугольника, a - основание треугольника, h - высота треугольника.
Зная площадь и высоту треугольника, можно найти основание, используя следующую формулу:
a = 2 * S / h.
Пример 1: Треугольник со сторонами 3, 4 и высотой 2.5
Рассмотрим пример треугольника со сторонами 3 и 4, а также с известной высотой, равной 2.5. С помощью высоты мы можем определить основание данного треугольника.
Для начала, вспомним геометрическое свойство высоты треугольника. Высота проведена из вершины треугольника до основания перпендикулярно этому основанию. Это означает, что она разделяет основание на две равные части.
Данная высота поделит основание на две отрезка, каждый из которых будет равен половине длины основания. Так как высота данного треугольника равна 2.5, а высота проведена перпендикулярно основанию, то основание будет состоять из двух равных отрезков длиной 2.5 каждый.
Итак, в нашем случае, основание будет состоять из двух отрезков длиной 2.5 каждый. Таким образом, мы определили основание треугольника по известной высоте и сторонам.
Пример 2: Равнобедренный треугольник со сторонами 5, высотой 4.8 и равными основаниями
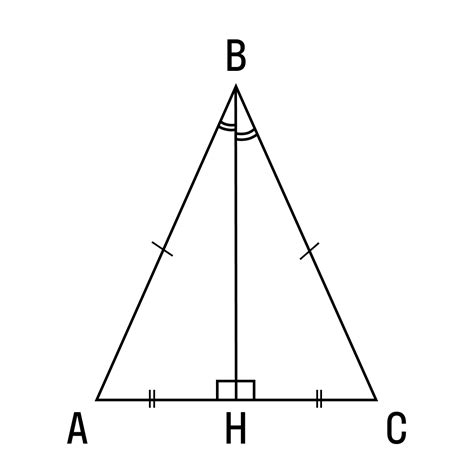
Так как треугольник равнобедренный, значит, его основания также равны. Чтобы определить длину основания, можно воспользоваться следующей формулой:
Основание = 2 * (Площадь треугольника) / Высота
Для нахождения площади треугольника, можно воспользоваться формулой:
Площадь = (Основание * Высота) / 2
Подставляя известные значения в формулу, получим:
Площадь = (Основание * 4.8) / 2
Так как треугольник равнобедренный, значит, его площадь можно найти по формуле прямоугольного треугольника:
Площадь = (Основание * Высота) / 2
Подставляя известные значения в формулу, получим:
Площадь = (Основание * 4.8) / 2
Чтобы найти основание треугольника, подставим известные значения в формулу:
5 = (Основание * 4.8) / 2
5 * 2 = Основание * 4.8
10 = Основание * 4.8
Основание = 10 / 4.8
Основание ≈ 2.08
Таким образом, в данном примере равнобедренный треугольник со сторонами 5, высотой 4.8 и равными основаниями имеет основание примерно равное 2.08.