Определение произведения векторов – одна из основных операций в линейной алгебре и геометрии. Оно позволяет находить новый вектор, который является результатом умножения двух векторов. Процесс определения произведения векторов основывается на двух основных принципах: коммутативности и дистрибутивности.
Принцип коммутативности гласит, что порядок умножения векторов не имеет значения. То есть, результат умножения вектора A на вектор B будет равен результату умножения вектора B на вектор A. Это свойство позволяет упростить вычисления и сократить количество необходимых операций.
Принцип дистрибутивности, в свою очередь, говорит о том, что умножение вектора на сумму векторов равно сумме умножений вектора на каждый из слагаемых суммы. То есть, (A + B) * C = A * C + B * C. Это правило позволяет разбить сложное выражение на более простые компоненты и упростить его решение.
Есть несколько способов определения произведения векторов: скалярное произведение и векторное произведение. Скалярное произведение векторов позволяет находить численное значение, которое показывает, насколько два вектора "похожи" друг на друга. Векторное произведение, в свою очередь, позволяет получить новый вектор, перпендикулярный плоскости, образованной двумя исходными векторами.
Векторные произведения: основные принципы

Основные принципы векторных произведений включают следующее:
| Принцип | Описание |
|---|---|
| Перпендикулярность | Векторное произведение двух векторов всегда перпендикулярно исходным векторам. Это означает, что угол между векторами-сомножителями составляет 90 градусов. |
| Правило левых рук | Для определения направления векторного произведения, можно использовать правило левой руки. Приложите вашу левую руку с изогнутым указательным и средним пальцами к началу первого вектора и поверните ладонь, чтобы указательный палец указывал в сторону второго вектора. Затем изогнутый палец будет указывать в направлении векторного произведения. |
| Длина | Длина векторного произведения равна площади параллелограмма, построенного на исходных векторах. Она рассчитывается с использованием формулы |A| * |B| * sin(θ), где A и B - исходные векторы, и θ - угол между ними. |
Понимание этих основных принципов векторных произведений поможет вам правильно определять направление, длину и перпендикулярность векторных произведений, что важно при решении различных физических и математических задач.
Что такое векторное произведение

Чтобы получить векторное произведение двух векторов, используется правило правой руки. Если указательный, средний и большой пальцы правой руки натянуты перпендикулярно друг к другу, то указательным пальцем можно указать направление векторного произведения. Если правая рука перевернута и указывает в другом направлении, векторное произведение будет иметь противоположное направление.
Векторное произведение имеет множество приложений в физике, геометрии и инженерии. Оно используется для определения момента силы, площади треугольника, проекции вектора и т.д. Векторное произведение также обладает свойством антикоммутативности, то есть результат векторного произведения двух векторов меняет знак при изменении порядка этих векторов.
Способы вычисления векторного произведения
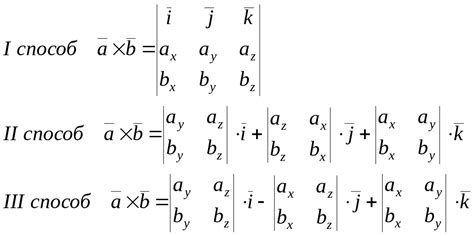
1. Геометрическое определение: для двух векторов a и b векторное произведение вычисляется как вектор, длина которого равна произведению длин векторов a и b на синус угла между ними, а направление определяется правилом правой руки.
2. Алгебраическое определение: векторное произведение вычисляется путем вычисления детерминанта трехмерной матрицы, составленной из координат исходных векторов.
| Примеры векторных произведений: | Геометрическое определение | Алгебраическое определение |
|---|---|---|
| a x b | ab sin(θ) n | i (aybz - azby) - j (axbz - azbx) + k (axby - aybx) |
| b x a | -ab sin(θ) n | -i (aybz - azby) + j (axbz - azbx) - k (axby - aybx) |
3. Векторные свойства: векторное произведение можно вычислить с использованием известных свойств векторов, таких как дистрибутивность, коммутативность и антикоммутативность.
Независимо от выбранного способа вычисления, векторное произведение имеет множество применений в физике, геометрии и механике. Оно позволяет находить площадь параллелограмма, определять направление момента силы, находить нормали к плоскостям и многое другое.
Практическое применение векторных произведений

- Геометрия: Векторные произведения используются для нахождения площади треугольников и объемов параллелепипедов. Также они позволяют определить направление нормали поверхности и расстояние между двумя параллельными прямыми.
- Физика: Векторные произведения применяются в законах электромагнетизма и механики. Например, они используются для нахождения силы Лоренца, момента силы и угла между двумя векторами скорости.
- Графика и компьютерное моделирование: Векторные произведения помогают определять ориентацию объектов в трехмерном пространстве, а также рассчитывать освещенность поверхностей при создании реалистичных изображений.
- Инженерия: Векторные произведения используются для анализа сил и моментов в механизмах, рассчета электромагнитных полей, проектирования антенн и многих других приложений.
В конечном счете, векторные произведения являются мощным математическим инструментом, который применяется в различных научных и технических областях. Они позволяют анализировать и моделировать физические процессы, а также решать реальные задачи, связанные с геометрией, физикой и инженерией.