Простые числа - это натуральные числа больше единицы, которые имеют только два делителя: единицу и само число. Они являются важными элементами в математике и имеют широкий спектр применений в криптографии, компьютерных алгоритмах и других областях. Определение простого числа является одной из фундаментальных задач теории чисел.
Существует несколько методов для определения простых чисел:
1. Перебор делителей: Самый простой способ определить, является ли число простым, - это перебрать все его делители от 2 до корня из числа. Если ни один из делителей не делит число без остатка, то число считается простым.
2. Решето Эратосфена: Этот метод основывается на идее удаления чисел, которые являются кратными простым числам. Сначала создается список всех чисел от 2 до заданного числа. Затем в списке удаляются все числа, начиная с первого простого числа, которые кратны этому числу. Процесс продолжается до тех пор, пока не останутся только простые числа.
3. Тест Ферма: Этот метод основывается на малой теореме Ферма. Если для заданного числа n выполняется условие a^(n-1) ≡ 1 (mod n) для всех a от 1 до n-1, то n с высокой вероятностью является простым числом. Однако, эта теорема не гарантирует полную точность.
Знание методов определения простых чисел является важным для различных областей математики и информатики. Оно позволяет проверять числа на простоту и использовать простые числа в различных приложениях и алгоритмах.
Определение простого числа

Для определения простого числа существует несколько методов. Один из самых простых и распространенных методов - это метод деления на множители. Суть этого метода заключается в том, что нужно проверить, делится ли данное число на какое-либо число из интервала от 2 до корня из самого числа. Если число не делится ни на одно из чисел из этого интервала, то оно является простым.
Другим методом определения простого числа является тест Миллера-Рабина. Этот тест позволяет проверить вероятность простоты числа на основе свойств простых чисел и быстро обнаруживает составные числа.
| Пример простых чисел |
|---|
| 2 |
| 3 |
| 5 |
| 7 |
| 11 |
Методы определения простых чисел являются важными в теории чисел и находят применение в различных областях, включая криптографию, генетику и алгоритмы поиска.
Методы проверки простоты числа

Существует несколько способов проверки простоты числа. Они могут быть различными по эффективности и сложности.
1. Перебор делителей
Этот метод заключается в переборе всех возможных делителей числа, начиная с 2 и заканчивая квадратным корнем из числа. Если при переборе найдется делитель, то число является составным. В противном случае, число является простым.
2. Решето Эратосфена
Этот метод основан на принципе исключения. Сначала создается массив чисел от 2 до n, где n - число, которое нужно проверить на простоту. Затем начинается процесс исключения: из массива удаляются все числа, кратные текущему числу, начиная с 2. После завершения процесса исключения, остаются только простые числа.
3. Тест Ферма
Суть этого теста заключается в том, что если n - простое число, то для любого целого a, такого что 1 < a < n, выполняется следующее равенство: a^(n-1) ≡ 1 (mod n). Если это равенство не выполняется, то число является составным. Но нужно быть осторожным, так как есть числа, для которых это равенство выполняется, но они составные. Такие числа называются числами Кармайкла.
4. Вероятностный тест Рабина-Миллера
Этот метод основан на свойствах простых чисел и модульной арифметики. Следует отметить, что он является вероятностным, то есть может дать неверный результат с некоторой вероятностью. Однако, при необходимости, его можно повторить несколько раз для увеличения точности.
Определение сложного числа

Для того чтобы определить, является ли число сложным, необходимо проверить, есть ли у него делители, отличные от 1 и самого числа. Если найдется хотя бы один такой делитель, то число считается сложным. В противном случае, если число не имеет делителей, кроме 1 и самого себя, то оно является простым.
Примеры сложных чисел: 4, 6, 8, 9, 10 и так далее.
Для определения сложного числа, можно использовать различные методы и алгоритмы, например, перебор всех возможных делителей, или применение алгоритма факторизации. Важно отметить, что определение сложного числа является важной задачей в математике, и имеет широкое практическое применение в криптографии, теории чисел и других областях.
Примеры сложных чисел

Ниже приведены несколько примеров сложных чисел:
1. Число 4
Число 4 можно разложить на множители 2 и 2. Поэтому оно является сложным числом.
2. Число 15
Число 15 можно разложить на множители 3 и 5. Поэтому оно также является сложным числом.
3. Число 27
Число 27 можно разложить на множители 3, 3 и 3. Значит, оно также является сложным числом.
Приведенные выше примеры демонстрируют, что все числа, у которых есть делители помимо 1 и самого числа, являются сложными числами.
Методы проверки числа на простоту

Для проверки числа на простоту существует несколько методов. Рассмотрим некоторые из них:
| Метод | Описание |
|---|---|
| Перебор делителей | Этот метод заключается в переборе всех чисел от 2 до корня из заданного числа и проверке их на делимость. Если найдется хотя бы один делитель, то число не является простым. |
| Решето Эратосфена | Этот метод основан на идее удаления всех чисел, кратных простым числам из заданного диапазона. В результате остаются только простые числа. |
| Тест Миллера – Рабина | Этот метод основан на использовании теста простоты Ферма и теста простоты Миллера – Рабина. Он более сложный, но эффективный для больших чисел. |
При выборе метода проверки числа на простоту необходимо учитывать его эффективность и требования к скорости выполнения.
Проверка делителей
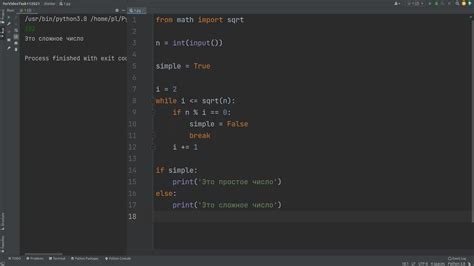
Проверка делителей основана на простом принципе: если у числа есть делитель, то этот делитель не может быть больше, чем корень из этого числа. Например, пусть мы проверяем число 25. Делители 25 - это 1, 5 и 25. Корень из 25 равен 5. Поэтому если мы не нашли делитель меньше или равный 5, то искомое число является простым.
Данный метод является достаточно эффективным для определения простых чисел в небольшом диапазоне. Однако для больших чисел требуется использование более сложных алгоритмов, таких как тест Миллера-Рабина или тест Люка-Лемера.
Примеры определения простого числа:

- Метод проверки делителей: число является простым, если оно не имеет делителей, кроме 1 и самого себя. Для проверки этого условия можно перебирать все числа от 2 до квадратного корня из заданного числа и проверять, делится ли исходное число на каждое из этих чисел без остатка.
- Метод решета Эратосфена: данный метод основан на идее последовательного вычеркивания всех составных чисел до заданного предела. Сначала создается список всех чисел от 2 до заданного предела, затем последовательно вычеркиваются все числа, кратные текущему числу. После прохода по всем числам останутся только простые числа.
- Метод Ферма: данный метод основан на тестировании всех чисел до заданного предела с помощью формулы a^(n-1) mod n, где a - случайное число от 2 до n-1, n - число для проверки. Если для всех чисел a формула возвращает 1, то число с большой вероятностью является простым.
Пример 1

Рассмотрим пример определения простого числа с помощью метода перебора делителей.
Допустим, нам нужно определить, является ли число 17 простым. Мы можем перебрать все числа от 2 до 16 и проверить, делится ли 17 на одно из них без остатка.
Начнем с делителя 2. Если 17 делится на 2 без остатка, то число 17 не является простым, так как оно делится на число, отличное от 1 и самого себя. Однако, мы видим, что 17 не делится на 2 без остатка.
Затем перейдем к делителю 3 и продолжим перебирать все числа до 16. Каждый раз мы будем проверять, делится ли 17 на текущий делитель без остатка.
Таким образом, мы убедимся, что 17 не делится на ни одно число от 2 до 16 без остатка. Следовательно, число 17 является простым.
Пример 2

Первым шагом мы делим число 37 на все числа от 2 до корня из 37 (округленного до ближайшего целого). Если число делится на любое из этих чисел без остатка, то оно не является простым.
| Делитель | 37 mod делитель |
| 2 | 1 |
| 3 | 1 |
| 4 | 1 |
| 5 | 2 |
| 6 | 1 |
| 7 | 2 |
| 8 | 5 |
| 9 | 1 |