Определение сторон при известном периметре статей является одной из важнейших задач в геометрии. Знание длин сторон позволяет решать различные задачи, связанные с нахождением площади, углов и других параметров фигур. В этой статье мы рассмотрим несколько методов и дадим советы, которые помогут вам определить стороны при известном периметре статей.
Первый и наиболее простой метод заключается в разделении периметра статей на количество сторон. Например, если у вас есть пятиугольник и известен его периметр, то можно разделить его на 5, чтобы найти длину каждой стороны. Этот метод применим не только к пятиугольникам, но и к многоугольникам с любым количеством сторон. Однако следует учитывать, что этот метод не всегда применим, особенно к сложным фигурам, в которых стороны имеют различную длину.
Второй метод основан на использовании треугольников. Как известно, сумма длин двух сторон треугольника всегда больше длины третьей стороны. Используя это свойство, можно построить несколько треугольников с двумя известными сторонами и определить длину третьей стороны. Затем можно использовать эти значения для определения длины остальных сторон. Этот метод позволяет достаточно точно определить стороны при известном периметре статей, особенно если известны углы, соответствующие этим сторонам.
Как определить стороны при известном периметре статей: базовые понятия
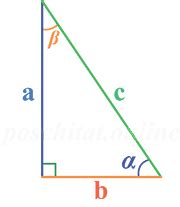
Для определения сторон при известном периметре статей необходимо знать форму фигуры. В зависимости от вида фигуры и количества сторон, которые она имеет, существуют различные подходы к решению данной задачи. Рассмотрим некоторые из них:
1. Квадрат. У квадрата все стороны равны между собой, поэтому для определения сторон мы можем просто разделить периметр на 4.
2. Прямоугольник. У прямоугольника две пары равных сторон. Если известны длины одной пары сторон, то по формуле периметра можно определить длину остальных сторон.
3. Треугольник. У треугольника все стороны могут быть разной длины. Для определения длины сторон при известном периметре можно использовать знания о свойствах разных типов треугольников, таких как равнобедренный треугольник или прямоугольный треугольник.
4. Другие многоугольники. Для более сложных фигур с большим количеством сторон (например, пятиугольник или шестиугольник) также можно использовать формулу периметра и свойства фигур, чтобы определить длины сторон.
Важно помнить, что возможный способ определения сторон зависит от предоставленной информации о фигуре и ее свойствах. При решении задачи по определению сторон при известном периметре статей полезно использовать знания о свойствах фигур и математические формулы.
Методы определения сторон при известном периметре статей

Метод 1: Расчет равных сторон
Если периметр статей известен и все стороны статей равны между собой, можно определить длину каждой стороны, разделив периметр на количество сторон. Например, если периметр составляет 12 см и статья имеет 3 стороны, каждая сторона будет длиной 4 см.
Метод 2: Расчет неравных сторон
Если периметр статей известен, но стороны статей не равны между собой, можно использовать систему уравнений для определения длины каждой стороны. Например, если периметр составляет 18 см и две стороны уже известны (5 см и 7 см), то третья сторона может быть найдена как разность периметра и суммы двух известных сторон (18 см - (5 см + 7 см) = 6 см).
Метод 3: Использование геометрических фигур
Можно использовать геометрические фигуры для определения сторон при известном периметре статей. Например, если периметр статьи составляет 20 см и она имеет форму прямоугольника, можно использовать формулу для периметра прямоугольника (P = 2 * (a + b)), где а и b - соседние стороны, чтобы определить длину каждой стороны.
В зависимости от конкретной ситуации и условий задачи можно выбрать наиболее подходящий метод для определения сторон при известном периметре статей.
Разделение периметра между сторонами

Один из самых простых способов - это равномерное разделение периметра между сторонами. Для этого мы делим общую длину периметра на количество сторон и получаем длину каждой стороны. Например, если у нас есть треугольник с периметром 12 см, то каждая сторона будет иметь длину 4 см (12 см / 3 стороны = 4 см).
Еще один метод - это использование пропорций. Если известно отношение длин двух сторон, мы можем использовать их пропорцию, чтобы найти длину каждой стороны. Например, если у нас есть прямоугольник со сторонами, отношение которых 2:3, и периметр равен 40 см, то мы можем установить пропорцию:
- 2 / (2 + 3) = x / 40,
- где x - это длина первой стороны.
Решив эту пропорцию, мы найдем, что первая сторона равна 16 см, а вторая сторона равна 24 см.
Еще один способ - это разбиение периметра на подразделы. Если у нас есть фигура с несколькими сторонами и известно, что периметр разделен на несколько сегментов, мы можем использовать эту информацию для определения длины каждой стороны. Например, если периметр шестиугольника разделен на три сегмента в отношении 2:3:4, и общий периметр равен 30 см, то мы можем установить пропорцию:
- 2 / (2 + 3 + 4) = x / 30,
- где x - это длина первого сегмента периметра.
Решив эту пропорцию, мы найдем, что первый сегмент периметра равен 6 см, второй сегмент равен 9 см, а третий сегмент равен 12 см. Зная длину каждого сегмента, мы можем определить длины соответствующих сторон.
Таким образом, для определения сторон при известном периметре мы можем использовать различные методы, включая равномерное разделение, использование пропорций и разбиение периметра на подразделы. Выбор метода зависит от специфики задачи и доступной информации.
Соотношение сторон треугольника с известным периметром
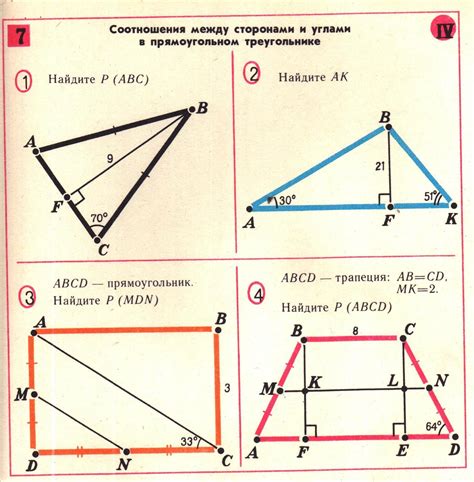
Одним из способов определить соотношение сторон треугольника с известным периметром является использование формулы для нахождения длин отдельных сторон. При известном периметре P и сторонах треугольника a, b и c формула имеет вид:
a + b + c = P
Таким образом, для определения длины каждой стороны треугольника необходимо разделить периметр на 3, что даст значение каждой отдельной стороны.
Кроме того, существуют специальные соотношения для некоторых видов треугольников, например, равносторонний или прямоугольный треугольник:
- В равностороннем треугольнике все стороны равны между собой, поэтому соотношение сторон равно 1:1:1.
- В прямоугольном треугольнике соотношение сторон может быть выражено с помощью теоремы Пифагора: a^2 + b^2 = c^2, где a и b - катеты, а c - гипотенуза треугольника.
Определение соотношения сторон треугольника с известным периметром позволяет более точно описать геометрическую структуру фигуры и использовать это знание в различных расчетах и задачах.
Поиск сторон в прямоугольнике с известным периметром
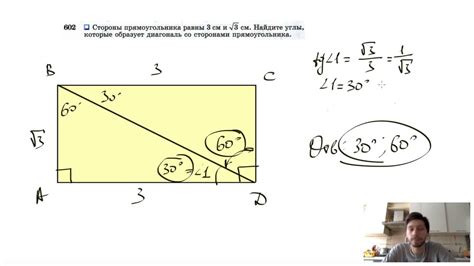
Если известен периметр прямоугольника и необходимо определить его стороны, нужно рассмотреть формулу для периметра и найти подходящие значения.
Периметр прямоугольника вычисляется по формуле: P = 2a + 2b, где P - периметр, a - длина одной стороны и b - длина другой стороны прямоугольника.
Чтобы найти значения сторон, следует решить уравнение с указанными параметрами:
P = 2a + 2b
Предположим, что периметр равен 20. Можно написать уравнение:
20 = 2a + 2b
Выразим одну из сторон через другую:
b = 10 - a
Теперь, заменим значение b в уравнении:
20 = 2a + 2(10 - a)
Раскроем скобки и сократим схожие члены:
20 = 2a + 20 - 2a
20 = 20
Уравнение выполняется, значит, длина сторон прямоугольника равна a = 10 и b = 10 - a = 10 - 10 = 0.
Таким образом, в прямоугольнике с периметром 20 одна сторона равна 10, а вторая сторона равна 0.
Не забывайте, что в реальной жизни стороны прямоугольника не могут быть отрицательными, поэтому такой пример, скорее всего, является теоретическим.
Определение сторон в квадрате с известным периметром
Основной шаг при определении сторон в квадрате с известным периметром – это определение значения периметра. Периметр квадрата вычисляется путем сложения всех его сторон или умножения длины одной стороны на 4.
Пример:
Допустим, у нас есть квадрат с периметром 20 см. Чтобы определить длину стороны, нам необходимо разделить периметр на 4: 20 см / 4 = 5 см. Полученное значение – 5 см – будет длиной каждой стороны этого квадрата.
Важно понимать, что периметр квадрата всегда будет кратен 4, так как все его стороны равны. Если периметр не является кратным 4, то это может быть признаком того, что у вас нет дела с квадратом, а, возможно, с другой фигурой.
Зная длину стороны квадрата, вы сможете проводить различные вычисления, такие как вычисление площади, нахождение диагонали и т.д.
Определение сторон в правильном многоугольнике
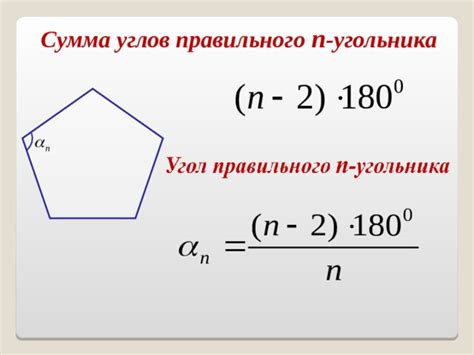
Длина стороны = Периметр / количество сторон.
Например, если у нас есть правильный треугольник с периметром 15 см, мы можем найти длину каждой стороны следующим образом:
Длина стороны = 15 см / 3 = 5 см.
Таким образом, каждая сторона правильного треугольника равна 5 см.
Аналогично, для правильного пятиугольника с периметром 20 см:
Длина стороны = 20 см / 5 = 4 см.
И каждая сторона правильного пятиугольника равна 4 см.
Таким образом, чтобы определить длину сторон в правильном многоугольнике, нужно разделить его периметр на количество сторон.
Примеры применения методов для определения сторон

Пример 1:
Допустим, у нас есть треугольник с известным периметром. Чтобы определить длины его сторон, можно использовать метод полупериметра. Полупериметр треугольника равен сумме длин его сторон, деленной на 2. Зная полупериметр и длину одной из сторон треугольника, можно вычислить длины оставшихся сторон с помощью формулы для нахождения площади треугольника по его сторонам и полупериметру.
Пример 2:
При определении сторон прямоугольника по известному периметру можно воспользоваться формулой, где периметр равен удвоенной сумме двух сторон прямоугольника. Зная периметр и длину одной из сторон, можно вычислить длину второй стороны, разделив периметр на два и вычесть из него длину известной стороны.
Пример 3:
Для определения сторон квадрата по известному периметру достаточно разделить периметр на 4, так как все стороны квадрата равны. Таким образом, длина каждой стороны будет равна периметру, деленному на 4.
Это лишь несколько примеров применения методов для определения сторон при известном периметре. В каждой конкретной задаче необходимо использовать соответствующий метод и формулу, учитывая условия задачи и известные данные. Важно иметь хорошее понимание математических принципов и геометрических свойств для успешного решения задач по определению сторон.
При определении сторон при известном периметре статей есть несколько методов и советов, которые могут помочь вам в этом процессе. Вот некоторые из них:
В первую очередь, необходимо знать, что периметр статьи – это сумма длин всех ее сторон. Используя эту информацию, можно приступить к определению длин отдельных сторон.
Один из методов – это разделение периметра на равные отрезки. Для этого можно разделить периметр статьи на количество равных отрезков, которые вы хотите получить. Например, если периметр статьи равен 20 см, а вы хотите разделить его на 4 равных отрезка, то каждый отрезок будет равен 5 см. Таким образом, вы определите длину каждой стороны.
Еще один метод – это определение длины одной стороны и вычисление длин остальных сторон. Например, если известно, что одна сторона статьи равна 6 см, а периметр статьи равен 20 см, то можно вычислить длины остальных сторон, исходя из того, что сумма всех сторон равна периметру. В данном случае длина оставшихся сторон будет равна 20 - 6 = 14 см, и так как все стороны равны между собой, то каждая из них будет иметь длину 14 / 3 = 4,67 см (округляем до двух десятичных знаков).
Кроме того, при определении сторон при известном периметре статей важно учитывать возможные ограничения, которые предопределены конкретной задачей или условием. Например, некоторые задачи могут требовать, чтобы все стороны были целыми числами или, наоборот, имели определенное количество десятичных знаков.