Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединены между собой. Но как узнать, можно ли по данным отрезкам построить треугольник? Существует несколько способов проверки.
Первый способ заключается в простом сравнении длин сторон треугольника. Для этого нужно взять любые две стороны и сложить их. Если сумма этих двух отрезков больше третьего отрезка, то треугольник будет существовать. Например, если имеются стороны длиной 3, 4 и 7 единиц, то условие выполняется: 3 + 4 = 7. Это значит, что треугольник с такими сторонами может быть построен.
Еще один способ проверки существования треугольника основан на использовании неравенства треугольника. Если для любых трех сторон выполняется условие, что сумма двух сторон больше третьей, то треугольник будет существовать. Например, для сторон длиной 3, 4 и 7 единиц: 3 + 4 > 7, 4 + 7 > 3 и 3 + 7 > 4. Все три неравенства выполняются, поэтому треугольник с такими сторонами может быть построен.
Существование треугольника по сторонам
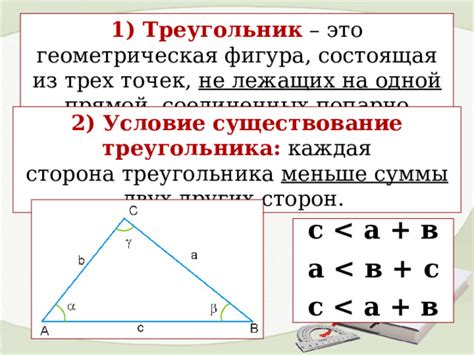
Существует некоторое правило, известное как неравенство треугольника, которое гласит, что сумма длин двух сторон треугольника всегда должна быть больше длины третьей стороны. Другими словами, для треугольника с сторонами a, b и c должно выполняться неравенство a + b > c, a + c > b и b + c > a.
Используя данное правило, можно определить, существует ли треугольник по заданным сторонам. Если неравенство выполняется для всех трех пар сторон, то треугольник существует. В противном случае, если хотя бы одно из неравенств не выполняется, треугольник невозможен.
Чтобы лучше понять и проиллюстрировать это, можно использовать таблицу:
| Сторона a | Сторона b | Сторона c | Существование треугольника |
|---|---|---|---|
| 2 | 3 | 4 | Да |
| 5 | 10 | 4 | Нет |
| 7 | 7 | 7 | Да |
Приведенная таблица демонстрирует различные комбинации сторон и указывает, является ли треугольник возможным или нет. Если в столбце "Существование треугольника" указано "Да", то треугольник с указанными сторонами существует, в противном случае указано "Нет".
Таким образом, для определения существования треугольника по заданным сторонам необходимо проверить, выполняются ли все три неравенства треугольника. Если все неравенства выполняются, то треугольник существует, иначе - нет.
Известные способы определения треугольника по сторонам
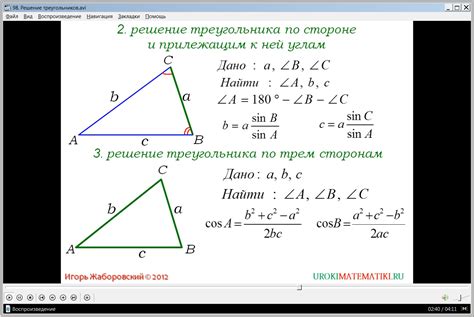
Существует несколько способов определить, можно ли по данным сторонам построить треугольник:
1. Неравенство треугольника: Если сумма двух сторон треугольника больше третьей стороны, то треугольник существует. Другими словами, для сторон a, b, c, треугольник существует, если выполняется неравенство a + b > c, a + c > b и b + c > a.
2. Теорема Пифагора: Если квадрат длины самой длинной стороны треугольника равен сумме квадратов длин двух других сторон, то треугольник прямоугольный. Если это равенство не выполняется, то треугольник не может быть прямоугольным.
3. Правило о трех сторонах: Если сумма двух сторон треугольника равна третьей стороне, то треугольник является вырожденным (имеет нулевую площадь) или треугольник не существует.
4. Правило о двух сторонах: Если сумма двух сторон треугольника меньше третьей стороны, то треугольник не может быть построен.
Используя эти способы, вы можете проверить, сможете ли вы построить треугольник по известным сторонам.
Условия для существования треугольника
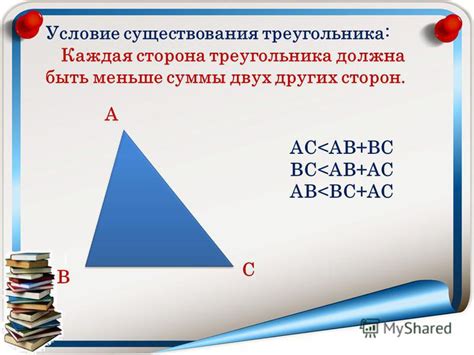
Для того чтобы треугольник существовал, должны выполняться определенные условия:
- Сумма любых двух сторон треугольника должна быть больше третьей стороны. Иначе говоря, если a, b и c - длины сторон треугольника, то выполняется следующее: a + b > c, a + c > b, b + c > a.
- Каждая сторона треугольника должна быть больше нуля. В противном случае треугольник не существует.
Если все указанные условия выполнены, то можно утверждать, что треугольник с такими сторонами существует.
Неравенство треугольника: ключевое правило
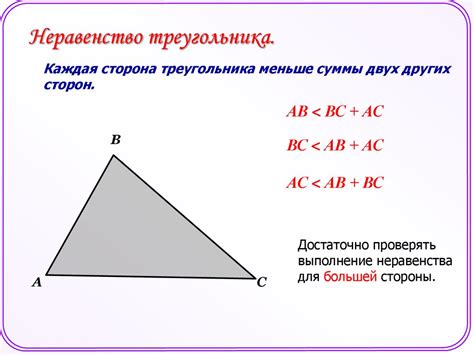
Для произвольного треугольника AВС:
Сумма длин любых двух сторон треугольника всегда должна быть больше длины третьей стороны.
Это правило важно помнить, чтобы избежать ошибок при определении существования треугольника по заданным сторонам.
Например, если заданы стороны треугольника АВС их длиной a, b и c, то условие неравенства треугольника можно записать следующим образом:
a + b > c
b + c > a
c + a > b
Если хотя бы одно из этих условий не выполняется, то треугольник по заданным сторонам нельзя построить.
Неравенство треугольника является фундаментальным свойством геометрических фигур и используется в различных областях, связанных с треугольниками.
Специальные случаи треугольников

Кроме обычных треугольников, которые можно определить по длинам их сторон, существуют специальные случаи треугольников, у которых есть дополнительные свойства.
Равносторонний треугольник: такой треугольник имеет три равные стороны и три равных угла. У всех углов равно по 60 градусов.
Равнобедренный треугольник: у такого треугольника есть две равные стороны и два равных угла. Третья сторона и третий угол могут быть различными.
Прямоугольный треугольник: один из углов такого треугольника равен 90 градусов. По теореме Пифагора, сумма квадратов длин катетов равна квадрату длины гипотенузы.
Остроугольный треугольник: у всех трех углов такого треугольника меньше 90 градусов.
Тупоугольный треугольник: в одном из углов такого треугольника больше 90 градусов.
Вырожденный треугольник: у такого треугольника сумма длин двух из его сторон равна длине третьей стороны, и все три стороны лежат на одной прямой. То есть, фактически это прямая.
Знание этих специальных случаев может быть полезным при анализе геометрических фигур и решении задач, связанных с треугольниками.
Основные свойства треугольника

1. Сумма внутренних углов:
В треугольнике сумма внутренних углов всегда равна 180 градусов. Это свойство называется также прямоугольностью треугольника.
2. Стороны и углы:
Треугольник определяется длинами его сторон и величинами его углов. Существует три типа треугольников:
- Равносторонний треугольник: все стороны равны, все углы равны 60 градусов.
- Равнобедренный треугольник: две стороны равны, два угла равны.
- Разносторонний треугольник: все стороны и углы разные.
3. Неравенство треугольника:
Сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Данное свойство позволяет определить, может ли существовать треугольник по заданным сторонам.
Практическая польза знания о существовании треугольника по сторонам

Знание о существовании треугольника по сторонам имеет широкий спектр применения в различных областях жизни:
1. Архитектура и строительство:
При проектировании и строительстве зданий и сооружений часто возникает необходимость рассчитать геометрические параметры, включая стороны треугольников. Знание о существовании треугольника по сторонам позволяет проектировщикам и инженерам точно определить геометрические свойства сооружений и обеспечить их прочность и устойчивость.
2. Геодезия и навигация:
При проведении линейных и геодезических измерений, а также при навигации часто возникает необходимость определить расстояния между точками и направления на ориентиры. Знание о существовании треугольника по сторонам позволяет геодезистам и навигационным специалистам точно определить позицию и ориентацию объектов на местности.
3. Инженерное дело:
В различных областях инженерии, таких как авиация, автомобилестроение, электротехника и т.д., знание о существовании треугольника по сторонам позволяет инженерам рассчитывать и прогнозировать различные физические параметры и свойства систем и устройств, включая силу, энергию, давление и другие величины.
4. Образование и наука:
Знание о существовании треугольника по сторонам является одним из фундаментальных элементов геометрии, которая широко применяется в математике, физике, компьютерной графике и других областях науки. Понимание треугольников по сторонам позволяет более глубоко изучать и понимать математические и физические концепции.
Таким образом, знание о существовании треугольника по сторонам имеет практическую пользу в различных областях жизни, включая архитектуру, строительство, геодезию, навигацию, инженерное дело, образование и науку.