Математика – это один из основных предметов, изучаемых в школе. Она дает нам мощный инструментарий для решения различных задач и анализа явлений в окружающем мире. Построение графиков функций – одно из ключевых понятий, которое помогает визуализировать и анализировать зависимость переменных между собой.

Процесс построения графика функции включает несколько шагов. Сначала нужно составить таблицу значений, определить диапазон изменения аргумента и построить координатную плоскость. Затем, используя полученные значения, необходимо отметить точки на графике и соединить их линиями.

Важно понимать, что график функции – это геометрическое представление математической зависимости. Изучая его, ученики могут лучше понять особенности функции, определить периодичность, экстремумы и другие характеристики функции. Это позволяет им шире и глубже взглянуть на мир чисел и выразить идеи и представления о нем с помощью графиков функций.

Как построить график функции в 7 классе

1. Определить область значений функции. Для этого нужно понять, какие значения переменной можно подставлять в функцию. Например, если функция задана для всех действительных чисел, то область значений будет неограниченной.

2. Построить таблицу значений функции. Чтобы построить график функции, нужно знать ее значения для различных значений переменной. Подставляйте разные значения переменной в функцию и вычисляйте соответствующие значения функции. Запишите полученные значения в таблицу.

3. Нанести точки на координатную плоскость. Для каждого значения переменной из таблицы значений нужно нанести точку на графике. Горизонтальная координата точки соответствует значению переменной, а вертикальная координата - значению функции.

4. Соединить точки линией. После нанесения всех точек на координатную плоскость, их нужно соединить линией. Ломаная линия соединяет все точки в порядке следования в таблице значений функции.

5. Добавить оси координат. Чтобы график функции был наглядным, нужно добавить оси координат. Они позволяют увидеть положение точек и ориентироваться на плоскости.

6. Подписать оси и график. Не забудьте подписать оси и сам график функции. На горизонтальной оси обычно указывают переменную, а на вертикальной оси - функцию. Также стоит подписать сам график, чтобы было понятно, какая функция изображена.

В результате выполнения всех этих шагов вы получите график функции. Он поможет вам лучше понять зависимость между переменной и функцией. Построение графиков функций является важным навыком для понимания математических концепций и может пригодиться в дальнейшем обучении.

Общие понятия и определения

Оси координат - это две перпендикулярные прямые, которые пересекаются в начале координат и используются для обозначения значений аргумента и значения функции. Горизонтальная ось называется осью x (ось абсцисс) и используется для обозначения значений аргумента. Вертикальная ось называется осью y (ось ординат) и используется для обозначения значений функции.

Точка на графике функции обозначает пару значений (x, y), где x - значение аргумента, а y - значение функции для данного аргумента.

Каждая функция имеет свои характерные особенности в построении графика. Например, если значение функции возрастает при увеличении аргумента, график функции будет направлен вверх. Если значение функции убывает при увеличении аргумента, график функции будет направлен вниз. Если значение функции остается одинаковым при изменении аргумента, график функции будет горизонтальной прямой.

Построение графика функции позволяет визуально анализировать ее свойства, такие как увеличение или убывание, максимум и минимум, пересечение с осями координат и другие характеристики. График функции является мощным инструментом для изучения и понимания математических отношений и зависимостей.

Практические примеры и упражнения

Для более глубокого понимания и закрепления навыков в построении графика функций в 7 классе, рекомендуется выполнить ряд практических примеров и упражнений.

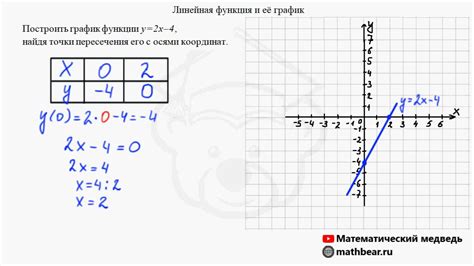
1. Построить график функции y = 2x + 3.

2. Найти область определения функции y = √(x - 1).

3. Построить график функции y = -x^2 + 4x - 3.

4. Найти корни уравнения y = 2x^2 - 5x + 3.

5. Построить график функции y = |x|.

Решение каждого примера и упражнения поможет усовершенствовать навыки в работе с графиками функций и проверить понимание основных понятий и правил.