График квадратичной функции является одним из важных инструментов в математике. Он позволяет наглядно представить зависимость между переменными и проявить основные характеристики функции. Построение графика квадратичной функции может быть полезным в различных областях, от математики до физики и экономики. В этой статье мы рассмотрим инструкцию и дадим несколько полезных советов о том, как построить график квадратичной функции.
Первый шаг, который необходимо сделать для построения графика квадратичной функции, - это определить ее уравнение. Квадратичная функция имеет вид y = ax^2 + bx + c, где a, b и c - это коэффициенты, которые определяют форму и положение графика. Коэффициент a отвечает за открытие и направление параболы, коэффициент b - за смещение по горизонтали, а коэффициент c - за смещение по вертикали.
Для построения графика квадратичной функции необходимо найти несколько точек на плоскости. Самые простые и удобные точки для определения графика - это вершина параболы и пересечение с осями координат. Чтобы найти вершину параболы, можно использовать формулу x = -b/2a. Подставив эту x-координату в уравнение квадратичной функции, можно найти соответствующую y-координату.
Построение графика квадратичной функции также требует определения направления и формы параболы. Если коэффициент a положительный, то парабола будет открыта вверх, а если отрицательный - парабола будет открыта вниз. Зная все эти характеристики, можно провести ось симметрии параболы, отразить ее относительно нее и провести саму параболу через точки, которые мы ранее нашли.
Как построить график квадратичной функции
Построение графика квадратичной функции может быть полезным для визуализации и понимания ее свойств и характеристик. Это позволяет наглядно увидеть, как меняется функция в зависимости от значений переменных.
Для построения графика квадратичной функции необходимо знать ее уравнение вида y = ax^2 + bx + c, где a, b и c - коэффициенты, определяющие форму и положение графика.
Шаги построения графика квадратичной функции:
1. Найти вершину графика. Вершина графика - это точка, в которой функция достигает экстремума. Координаты вершины можно найти с помощью формулы x = -b/2a и подставить найденное значение в уравнение для нахождения y.
2. Найти дополнительные точки. Для построения графика квадратичной функции полезно найти еще несколько точек, чтобы лучше понять ее форму и поведение. Дополнительные точки можно найти, подставив разные значения x в уравнение и вычислив соответствующие значения y.
3. Построить оси координат. График квадратичной функции проходит через начало координат, поэтому необходимо построить горизонтальную ось (ось x) и вертикальную ось (ось y).
4. Построить график. Используя найденные точки, соедините их линией, чтобы получить график квадратичной функции. Вершина функции будет являться точкой экстремума, а форма графика будет определяться коэффициентами a, b и c.
5. Проанализировать график. Построенный график позволяет анализировать различные свойства квадратичной функции, такие как направление открывания параболы, наличие экстремума, а также интервалы возрастания и убывания функции.
Построение графика квадратичной функции является важным инструментом для изучения и анализа ее свойств. Следуя указанным шагам, вы сможете легко построить график и лучше понять поведение функции в зависимости от изменения переменных.
Подготовка к построению графика квадратичной функции
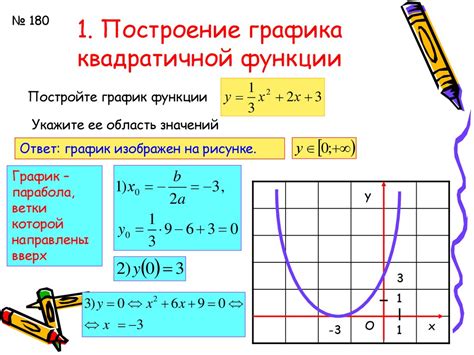
- Определение области определения: перед началом построения графика необходимо определить область определения заданной квадратичной функции. Область определения может быть ограничена, поэтому важно учесть все условия.
- Нахождение вершины параболы: вершина параболы играет важную роль при построении графика квадратичной функции. Чтобы найти вершину, можно воспользоваться формулой: x = -b / (2a), где a и b – коэффициенты квадратичной функции.
- Анализ знака коэффициента a: знак коэффициента a определяет, как будет выглядеть парабола – ветви направлены вверх или вниз. Если a положительное, то парабола будет направлена вверх, если отрицательное – вниз.
- Нахождение точек пересечения с осями координат: чтобы построить график квадратичной функции, необходимо найти точки пересечения параболы с осями координат. Для этого можно приравнять функцию к нулю и решить получившееся квадратное уравнение.
- Определение симметрии параболы: симметричность параболы относительно вертикальной прямой, проходящей через ее вершину, позволяет построить только одну половину графика. Учитывая это, мы можем построить симметричную относительно вершины параболу, отражая ее справа налево.
- Построение графика: после выполнения всех предыдущих шагов можно приступить к построению графика квадратичной функции. Используя значения функции в разных точках, полученные на предыдущих этапах, можно построить гладкую кривую, отображающую форму параболы на координатной плоскости.
Следуя указанным шагам, вы сможете успешно построить график квадратичной функции. Не забывайте, что практика играет важную роль в овладении навыком построения графиков, поэтому регулярное тренирование поможет вам стать более уверенным в этом процессе.
Определение осей и масштаба графика
Для построения графика квадратичной функции необходимо правильно определить оси координат и масштаб графика. Определение осей поможет нам установить границы графика на плоскости, а масштаб позволит нам корректно отобразить значения функции.
Оси координат состоят из вертикальной оси (ось ординат) и горизонтальной оси (ось абсцисс). Ось ординат обозначается буквой y, а ось абсцисс - буквой x. Они пересекаются в точке, называемой началом координат и обозначаемой буквой O.
Для определения масштаба графика необходимо выбрать шаг по осям. Шаг - это расстояние между двумя соседними делениями на оси. Чтобы выбрать подходящий шаг, нужно учитывать диапазон значений функции и доступное пространство на графике.
| Ось | Масштаб |
|---|---|
| Ось ординат (y) | Выберите шаг, учитывая диапазон значений функции по оси y и размер графика |
| Ось абсцисс (x) | Выберите шаг, учитывая диапазон значений аргумента функции по оси x и размер графика |
Определение осей и масштаба графика является важным этапом при построении графика квадратичной функции. Он позволяет нам визуализировать функцию на плоскости и анализировать ее свойства.
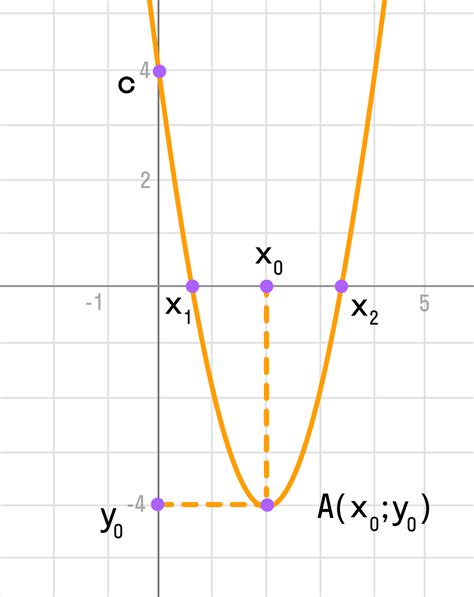
Нахождение вершины и осей симметрии графика
График квадратичной функции имеет форму параболы и может быть описан уравнением вида:
$y = ax^2 + bx + c$
Для построения графика необходимо знать коэффициенты $a$, $b$ и $c$, а также найти вершину и оси симметрии.
Вершина параболы имеет координаты $(x_0, y_0)$, где:
- $x_0 = -\frac{b}{2a}$ - координата вершины по оси $x$
- $y_0 = f(x_0) = a(x_0)^2 + b(x_0) + c$ - координата вершины по оси $y$
Ось симметрии - это прямая, перпендикулярная оси $x$, проходящая через вершину параболы. Ось симметрии является вертикальной прямой и имеет уравнение:
$x = x_0$
Таким образом, используя вышеуказанные формулы, можно найти вершину и ось симметрии графика квадратичной функции.
Построение графика и анализ зависимости
| Шаг | Действие |
|---|---|
| 1 | Запишите квадратичную функцию в стандартной форме: y = ax^2 + bx + c, где a, b и c - коэффициенты функции. |
| 2 | Определите значения x, для которых хотите построить график. Запишите эти значения в виде таблицы. |
| 3 | Вычислите соответствующие значения y для каждого заданного x с помощью квадратичной функции. |
| 4 | Изобразите на координатной плоскости точки с координатами (x, y), полученные на предыдущем шаге. |
| 5 | Соедините точки гладкой кривой, которая будет представлять график квадратичной функции. |
После построения графика квадратичной функции можно проанализировать её зависимость. Например, по графику можно определить, имеет ли функция вершину вниз или вверх и определить её координаты. Также можно выявить особенности ветвей функции и определить, где она пересекает оси координат. График помогает визуализировать поведение функции в зависимости от её коэффициентов и переменных.