Описанная окружность треугольника - это окружность, которая проходит через все три вершины треугольника. Она является одним из важных элементов в геометрии и находит применение как в математике, так и в реальной практике.
Построение описанной окружности треугольника возможно при помощи различных методов и инструментов. Один из простых способов - использование перпендикуляров, опущенных из середин сторон треугольника. Другой метод основан на использовании углов треугольника и их свойств.
Для построения описанной окружности треугольника можно использовать как традиционные инструменты (линейку, циркуль), так и современные компьютерные программы для геометрических расчётов. Описанная окружность имеет множество применений, например, в разработке архитектурных проектов, строительстве, геодезии, картографии, машиностроении и других областях, где требуется точное определение координат и расстояний.
В данной статье мы рассмотрим несколько примеров из реальной практики, где построение описанной окружности треугольника имеет важное значение. Будут рассмотрены примеры из области строительства и геодезии, которые помогут вам лучше понять и применить этот элемент в своей работе.
Описание окружности треугольника
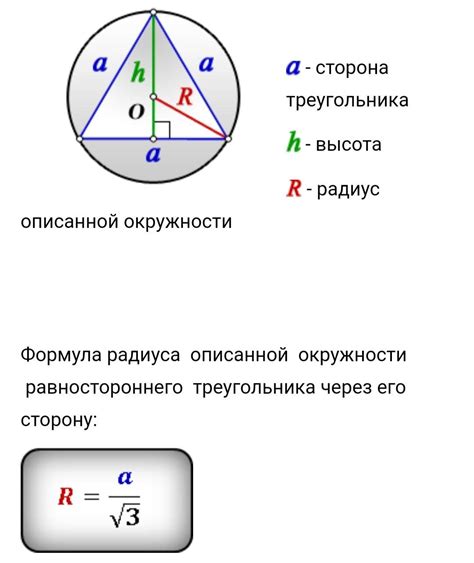
Для того чтобы построить описанную окружность треугольника, необходимо найти центр описанной окружности и радиус, который определяется расстоянием от центра до любой из вершин треугольника. Существует несколько способов построения описанной окружности треугольника.
Один из способов основан на использовании перпендикуляров, проведенных из середин сторон треугольника до противоположных вершин. Точка пересечения этих перпендикуляров будет являться центром окружности, а расстояние от центра до любой вершины треугольника будет равно радиусу описанной окружности.
Другой способ состоит в использовании точек пересечения биссектрис треугольника. Биссектрисы треугольника пересекаются в одной точке, которая является центром описанной окружности. Радиус окружности будет равен расстоянию от центра до любой вершины треугольника.
Описанная окружность треугольника обладает рядом интересных свойств. Например, середины сторон треугольника лежат на окружности, а углы, образованные хордами, равны половине центрального угла, соответствующего этим хордам.
Понимание способов построения и свойств описанной окружности треугольника является важным элементом геометрических вычислений и может быть полезным при решении различных задач, связанных с треугольниками и окружностями.
Что такое описанная окружность треугольника
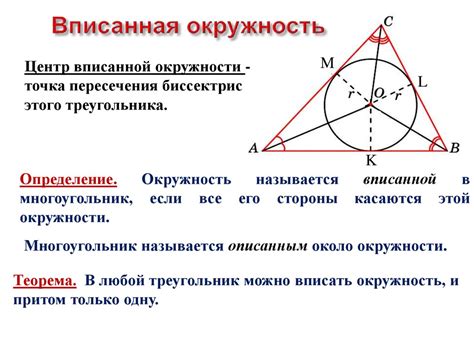
Для того чтобы построить описанную окружность треугольника, необходимо найти центр окружности и ее радиус. Центр окружности лежит на перпендикуляре, опущенном из середины стороны треугольника, а радиус равен половине длины этой стороны.
Описанная окружность треугольника имеет множество свойств, которые часто используются в геометрии. Например, длина хорды, проведенной на этой окружности, равна произведению радиуса на тангенс половины соответствующего центрального угла. Также, если из одной точки внутри треугольника провести линии, соединяющие эту точку с вершинами треугольника, то точка пересечения этих линий будет лежать на описанной окружности треугольника.
Описанная окружность треугольника широко применяется в различных областях, таких как математика, физика, компьютерная графика и дизайн. Она является важным инструментом для решения различных задач и построения геометрических конструкций.
Построение описанной окружности через окружность Эйлера
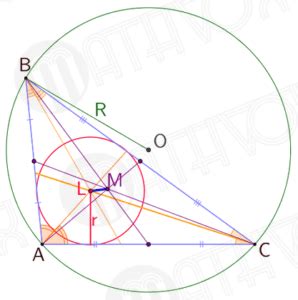
Окружность Эйлера – это окружность, проходящая через основания высот и середины сторон треугольника. Для построения описанной окружности через окружность Эйлера, нужно следовать следующим шагам:
- Построение высот треугольника: Проведите высоты треугольника из каждой вершины к противоположной стороне. В итоге вы получите точки пересечения высот, образующие окружность Эйлера.
- Построение середин сторон: Найдите середины каждой стороны треугольника.
- Проведение окружности через точки пересечения и середины сторон: Проведите окружность, проходящую через точки пересечения высот и середины сторон треугольника. Эта окружность будет описанной окружностью треугольника.
Построение описанной окружности через окружность Эйлера является одним из методов, который позволяет легко и точно определить положение описанной окружности относительно треугольника. Этот метод широко используется в геометрии и строительстве для решения различных задач и построений.
Примеры описанных окружностей в геометрических конструкциях
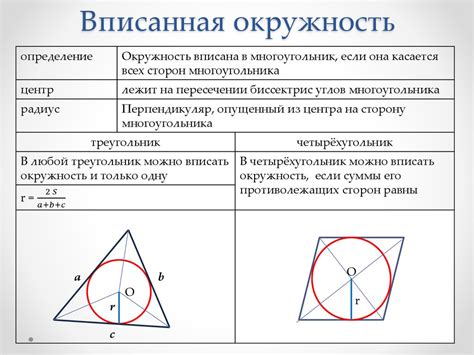
1. Треугольники Паскаля. Описанная окружность треугольников Паскаля - это окружность, проходящая через вершины треугольников Паскаля, которые образуются при построении треугольника из биномиальных коэффициентов. Описанная окружность треугольников Паскаля имеет интересные свойства и используется, например, в теории вероятностей и комбинаторике.
2. Окружность Эйлера. Описанная окружность треугольника Эйлера - это окружность, проходящая через середины сторон треугольника Эйлера и центр описанной окружности исходного треугольника. Описанная окружность треугольника Эйлера используется в различных геометрических конструкциях, включая построение эксцентров треугольника.
3. Квадратичные диаграммы. В графическом представлении квадратичных диаграмм, описанная окружность является важным элементом. Квадратичные диаграммы используются, например, в математическом анализе и теории оптимизации для визуализации квадратичных функций и их свойств.
Примеры описанных окружностей в геометрических конструкциях демонстрируют, как это понятие играет роль в различных областях математики и науки. Описанная окружность треугольника имеет много интересных свойств и может быть использована для решения различных задач и построений.
Применение описанных окружностей в инженерии и архитектуре
Одним из применений описанных окружностей в инженерии является проектирование и строительство дорог. При проектировании дорожных развязок и кривых участков дороги, знание описанных окружностей позволяет инженерам стабильно определять различные параметры, такие как радиус поворота и угол поворота, что важно для безопасного движения автотранспорта.
В архитектуре описанные окружности применяются для создания уникальных и гармоничных форм зданий и сооружений. Архитекторы могут использовать описанную окружность для разработки планов зданий, определения расположения дуг и сводов, а также для создания эффектных фасадов.
Кроме того, описанные окружности в инженерии и архитектуре могут быть применены в вычислительной геометрии. Математические модели, основанные на описанных окружностях, позволяют инженерам и архитекторам эффективно решать сложные задачи, связанные с определением точного положения объектов и проведением точных измерений.
Таким образом, описанные окружности играют важную роль в инженерии и архитектуре, помогая создавать безопасные и эстетически привлекательные сооружения, а также решать сложные геометрические задачи.