Треугольник - это одна из самых простых и известных геометрических фигур. Он образуется тремя отрезками, которые называются сторонами треугольника. Но как гарантированно построить треугольник по заданным сторонам? В этой статье мы расскажем вам об этом подробнее.
Для построения треугольника нужно знать длины всех его сторон. Это основное условие, которое необходимо выполнить. Если у вас есть эти данные, то вы можете перейти к следующему шагу.
Перед тем как приступить к построению треугольника, важно провести проверку возможности его существования. Существует такое правило: сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. Если данное условие не выполняется, то треугольник с такими сторонами построить невозможно.
Основные понятия
При построении треугольника по трем сторонам важно знать следующие основные понятия:
- Стороны треугольника: каждая сторона треугольника образуется между двумя его вершинами.
- Вершины треугольника: точки пересечения сторон треугольника.
- Углы треугольника: области или пространства между сторонами треугольника.
- Биссектриса: прямая, которая делит угол на две равные части.
- Периметр треугольника: сумма длин всех трех его сторон.
- Полупериметр треугольника: половина суммы длин всех его сторон.
- Высота треугольника: проведенная перпендикулярно к одной из сторон треугольника из противоположной вершины.
- Площадь треугольника: площадь, ограниченная треугольником.
- Треугольник со строго прямым углом: треугольник, у которого один из его углов равен 90 градусов.
- Треугольник равнобедренный: треугольник, у которого две его стороны равны.
- Треугольник равносторонний: треугольник, у которого все его стороны равны.
- Треугольник разносторонний: треугольник, у которого все его стороны различны.
Понимание этих основных понятий поможет правильно построить треугольник по трем сторонам и провести различные дополнительные построения и расчеты в геометрии.
Инструменты для построения треугольника
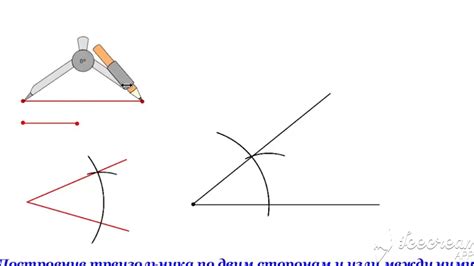
При построении треугольника, помимо знания длин сторон, полезно использовать некоторые инструменты и методы, которые помогут в достижении точности и превосходных результатов.
1. Линейка: Инструментом, без которого не обойтись при построении треугольника, является линейка. С ее помощью можно измерить и отметить длины сторон треугольника, а также провести прямые линии с нужными углами.
2. Транспортир: Для определения и построения углов треугольника, полезно использовать транспортир. С его помощью можно точно измерить и нарисовать углы треугольника.
3. Карандаш и ластик: Использование карандаша и ластика позволяет осуществлять предварительные отметки и корректировать погрешности при необходимости.
4. Интернет-ресурсы: Существуют онлайн-инструменты и приложения, которые помогают строить треугольники с использованием ввода значений сторон или измерений. Они могут быть полезны, если у вас нет необходимых инструментов или вам нужно быстро и легко построить треугольник.
Не забывайте, что при построении треугольника важно быть внимательным, следить за точностью измерений и проведения линий. Используйте данные инструменты и методы для достижения наилучших результатов при построении треугольника.
Шаги построения

Для того чтобы построить треугольник по заданным сторонам, следуйте следующим шагам:
1. Нарисуйте отрезки, соответствующие длинам заданных сторон, используя линейку и карандаш. Обозначьте эти отрезки как AB, BC и AC.
2. Выберите одну из сторон, например AB, и используйте ее в качестве базовой стороны треугольника. На противоположной стороне AC отметьте точку D.
3. С помощью циркуля и компаса проведите дугу с центром в точке D и радиусом BC, чтобы получить точку E на продолжении AB.
4. Соедините точки B и E отрезком.
5. С помощью циркуля и компаса проведите дугу с центром в точке B и радиусом AC, чтобы получить точку F на продолжении BC.
6. Соедините точки C и F отрезком.
Важно: Убедитесь, что отрезки BE и CF имеют одинаковую длину, чтобы треугольник ABC был соответствующим треугольником с заданными сторонами.
После завершения этих шагов вы получите построенный треугольник ABC, у которого длины сторон соответствуют заданным значениям AB, BC и AC.
Шаг 1: Расчет углов треугольника
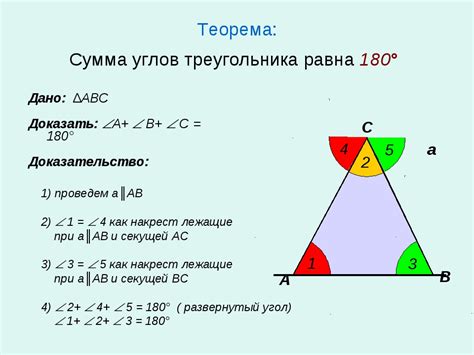
Перед тем как построить треугольник по трем сторонам, необходимо вычислить значения его углов. Для этого можно воспользоваться теоремой косинусов или теоремой синусов.
Теорема косинусов позволяет найти углы треугольника, если известны длины его сторон. Формула для расчета угла A выглядит следующим образом:
cos(A) = (b^2 + c^2 - a^2) / (2bc)
где a, b, и c - длины сторон треугольника, а A - угол противолежащий стороне a.
Таким образом, для расчета углов треугольника необходимо взять каждую сторону и применить формулу косинусов, чтобы найти все три угла.
Теорема синусов также позволяет вычислить углы треугольника, но в этом случае нужно знать длины сторон и соответствующие им противолежащие углы. Формула для расчета угла A выглядит следующим образом:
sin(A) = (a / c) * sin(C)
где A - угол противолежащий стороне a, C - противолежащий угол, a - длина стороны, c - длина противолежащей стороны.
Таким образом, если известны длины сторон и соответствующие противолежащие углы, можно использовать формулу синусов для расчета углов треугольника.
После выполнения этих математических операций, у вас будет полная информация о углах треугольника - вы готовы переходить к следующему шагу, а именно, построению треугольника по трем сторонам.
Шаг 2: Расчет длин сторон треугольника
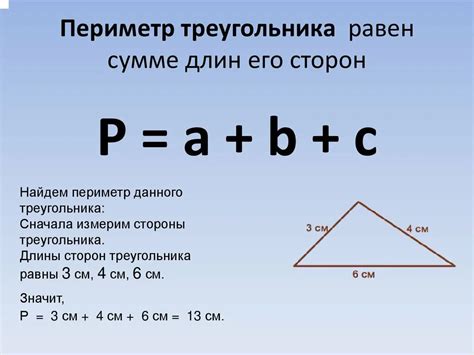
После выбора трех сторон треугольника необходимо провести расчет их длин. Это важный шаг, так как длины сторон будут определять форму и размеры треугольника.
Для расчета длин сторон можно использовать теорему Пифагора. Согласно этой теореме, сумма квадратов длин катетов прямоугольного треугольника равна квадрату гипотенузы.
Для не прямоугольного треугольника можно использовать формулу Герона. Данная формула позволяет найти площадь треугольника, зная длины всех его сторон. С помощью площади и длин сторон можно получить длины высот, медиан и биссектрис треугольника.
При расчете стоит обратить внимание на единицы измерения. Длины сторон обычно измеряются в сантиметрах (см) или метрах (м). Убедитесь, что используете одну и ту же единицу для всех сторон.
Важно быть внимательным при проведении вычислений, чтобы избежать ошибок и получить правильные значения длин сторон треугольника.
Шаг 3: Построение треугольника по заданным параметрам

После определения длин сторон треугольника, мы можем перейти к его построению. Для этого необходимо:
- Нарисовать отрезки, соответствующие длинам сторон. На плоскости можно использовать линейку и карандаш для этого шага. Начните с выбора точки начала отрезка, а затем отмерьте необходимую длину и нарисуйте отрезок.
- Соединить концы отрезков. Этот шаг представляет собой соединение отрезков вместе, чтобы образовать треугольник. Для этого вы можете использовать линейку или просто нарисовать линию, соединяющую все концы отрезков.
После выполнения этих двух шагов, вы получите построенный треугольник на плоскости, используя заданные параметры. Убедитесь, что полученная фигура имеет три стороны и три угла, и соответствует данным, которые вы использовали для построения.
Замечание: если длины сторон не соответствуют правилам построения треугольника, построение может быть невозможно. В этом случае вам потребуется изменить длины сторон или использовать другие методы для построения треугольника.
Примеры построения
Рассмотрим несколько примеров построения треугольника по трем сторонам.
Пример 1:
- Выберите произвольную линейку и отложите на ней первую сторону треугольника.
- Выберите точку на линейке, соответствующую второй стороне треугольника, и поставьте там острие компаса.
- Сделайте дугу, используя для радиуса расстояние, равное третьей стороне треугольника.
- Поставьте острие компаса в точку пересечения дуги и линейки.
- Нарисуйте линию, соединяющую начальную точку и точку пересечения дуги и линейки - это третья сторона треугольника.
Пример 2:
- На линейке отложите первую сторону треугольника.
- Закрепите уголок адаптера к точке отложенной первой стороны треугольника.
- Повторите эти действия для второй стороны треугольника.
- Оставшийся конец адаптера будет указывать на третью сторону треугольника - его можно отметить.
Пример 3:
- Выберите точку на бумаге - это будет одна из вершин треугольника.
- Отметьте вторую вершину треугольника на некотором расстоянии от первой.
- Используя линейку, соедините первую и вторую вершины и продолжите линию за ее пределы.
- Отметьте третью вершину треугольника на пересечении продолженной линии и другой линии.
Следуя подобным методам, вы можете построить треугольник по трем сторонам. Убедитесь, что ваши измерения точны, чтобы получить корректную форму треугольника.
Пример 1: Построение треугольника по известным сторонам
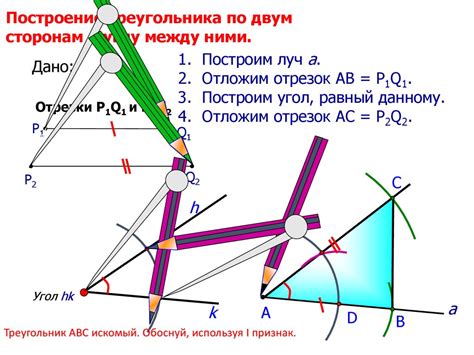
Для построения треугольника по известным сторонам нужно выполнить следующие шаги:
- Измерьте длины трех сторон треугольника с помощью линейки или машины для измерения длины.
- Выберите самую длинную сторону и назовите ее основой треугольника.
- Отложите на основе треугольника отрезок, равный длине второй стороны.
- Разместите ластика на конце отрезка и установите радиус ластика равным длине третьей стороны.
- Поворачивайте ластик вокруг точки, где он касается основы треугольника, пока он не коснется первой точки на основе треугольника. Третья точка, где ластик пересекает основу треугольника, будет вершиной треугольника.
Теперь вы можете нанести отрезки между вершинами треугольника, чтобы закончить его конструкцию.