Сопротивление в электрической схеме - одна из основных характеристик, которая определяет сложность в расчетах и эффективность ее работы. Перед тем как приступить к расчетам, необходимо определить общее сопротивление цепи - сумму всех сопротивлений, подключенных к ней.
Рассчитывая общее сопротивление, важно учитывать как активное, так и реактивное сопротивление. Активное сопротивление характеризует силу сопротивления, испытываемую электрическим током, тогда как реактивное сопротивление связано с изменением напряжения в конденсаторах и катушках индуктивности в электрической цепи.
Сопротивление в проводнике можно рассчитать с помощью закона Ома, который устанавливает пропорциональную зависимость между силой тока и напряжением: R = U/I. Здесь R - сопротивление, U - напряжение, а I - сила тока.
Для определения общего сопротивления цепи, вам потребуются знания о параллельном и последовательном соединении сопротивлений. При последовательном соединении сопротивлений, общее сопротивление равно сумме всех индивидуальных сопротивлений. При параллельном соединении, обратное значения сопротивления равно сумме обратных величин каждого сопротивления, а общее сопротивление можно вычислить обратившись к закону Ома.
Определение общего сопротивления
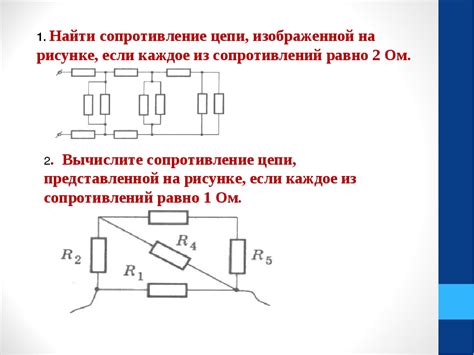
Для нахождения общего сопротивления необходимо знать значения сопротивлений каждого резистора в цепи. Если в цепи присутствуют параллельно соединенные резисторы, то сначала необходимо найти их эквивалентное сопротивление, а затем сложить его с сопротивлением резисторов, соединенных последовательно.
Если в цепи присутствуют только сопротивления, соединенные последовательно, то общее сопротивление вычисляется путем простого сложения значений сопротивлений. Для этого можно использовать формулу:
Общее сопротивление (Rобщ) = R1 + R2 + ... + Rn
где R1, R2, ..., Rn - значения сопротивлений каждого резистора в цепи.
| Сопротивление (R) | Единица измерения |
|---|---|
| Ом | Ω |
Теперь, когда вы знаете, как определить общее сопротивление, вы сможете успешно выполнять расчеты в электрических цепях и применять полученные значения для решения различных задач.
Формула для расчета

Общее сопротивление двух или более резисторов, подключенных последовательно, можно рассчитать с помощью следующей формулы:
Rобщ = R1 + R2 + ... + Rn
где Rобщ - общее сопротивление соединения;
R1, R2, ..., Rn - сопротивления каждого резистора, подключенного в последовательность.
Если в цепи имеются резисторы, подключенные параллельно, расчет общего сопротивления будет немного отличаться:
1/Rобщ = 1/R1 + 1/R2 + ... + 1/Rn
где Rобщ - общее сопротивление соединения;
R1, R2, ..., Rn - сопротивления каждого резистора, подключенного параллельно.
Используя эти формулы, вы сможете точно рассчитать общее сопротивление цепей с любым количеством резисторов, подключенных последовательно или параллельно.
Как работать с последовательным сопротивлением

1. Определите количество резисторов, соединенных последовательно в цепи. Это может быть любое количество резисторов, но они должны быть подключены друг за другом без несоединенных узлов.
2. Измерьте сопротивление каждого резистора с помощью мультиметра. Запишите значения сопротивлений для последующего использования.
3. Сложите значения сопротивлений всех резисторов вместе. Это даст вам общее сопротивление последовательного соединения. Например, если у вас есть резисторы с сопротивлением 10 Ом, 20 Ом и 30 Ом, то общее сопротивление будет равно 10 Ом + 20 Ом + 30 Ом = 60 Ом.
4. Учтите учет влияния кабелей и контактов на общее сопротивление. Если у вас есть дополнительные провода или соединения, учитывайте их сопротивление при расчете общего сопротивления.
Теперь у вас есть все необходимые знания, чтобы работать с последовательным сопротивлением. Помните, что общее сопротивление будет равно сумме сопротивлений всех резисторов, подключенных последовательно в цепи, плюс сопротивление проводов и контактов. Эти знания помогут вам эффективно работать с электрическими цепями и решать различные задачи, связанные с сопротивлением.
Как работать с параллельным сопротивлением

Когда имеется несколько сопротивлений, соединенных параллельно, общее сопротивление может быть рассчитано с помощью формулы. Общее сопротивление в параллельном соединении можно найти с использованием следующей формулы:
1/Общее сопротивление = 1/Сопротивление1 + 1/Сопротивление2 + 1/Сопротивление3 + ...
Пример:
Если у нас есть два сопротивления, Сопротивление1 равное 4 Ом и Сопротивление2 равное 6 Ом, мы можем рассчитать общее сопротивление.
1/Общее сопротивление = 1/4 + 1/6 = 3/12 + 2/12 = 5/12
Общее сопротивление будет равно:
Общее сопротивление = 12/5 Ом
Рассчитав общее сопротивление, мы можем использовать его в дальнейшем анализе электрической цепи или при расчетах тока и напряжения.
Теперь вы знаете, как работать с параллельным сопротивлением и как найти общее сопротивление в параллельной схеме.
Сочетание последовательного и параллельного сопротивления
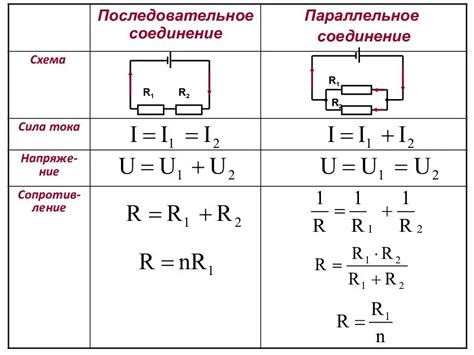
При решении практических задач часто возникает необходимость вычислить общее сопротивление цепи, в которую входят как последовательное, так и параллельное сопротивления. Для решения таких задач необходимо знать законы комбинирования сопротивлений.
При сочетании последовательного и параллельного сопротивлений общее сопротивление можно вычислить с помощью формулы:
1/Rekv = 1/R1 + 1/R2 + ... + 1/Rn
где Rekv - общее сопротивление цепи, R1, R2, ..., Rn - значения соответствующих сопротивлений. При этом, если в цепи присутствует только последовательное или только параллельное соединение, то соответствующие слагаемые в формуле равны нулю.
При наличии последовательного соединения общее сопротивление равно сумме всех сопротивлений в цепи:
Rekv = R1 + R2 + ... + Rn
При наличии параллельного соединения общее сопротивление можно рассчитать по следующей формуле:
Rekv = 1/(1/R1 + 1/R2 + ... + 1/Rn)
Зная значения сопротивлений в цепи, можно применить эти формулы для нахождения общего сопротивления. Таким образом, сочетание последовательного и параллельного сопротивлений позволяет моделировать различные электрические схемы и решать различные задачи в электротехнике.
Примеры расчетов

В данном разделе приведены несколько примеров расчетов общего сопротивления для различных электрических цепей.
Пример 1:
Рассмотрим простую электрическую цепь, состоящую из двух резисторов, подключенных последовательно.
- Резистор 1: R1 = 5 Ом
- Резистор 2: R2 = 10 Ом
Общее сопротивление цепи можно рассчитать с помощью формулы:
R = R1 + R2 = 5 Ом + 10 Ом = 15 Ом
Пример 2:
Рассмотрим цепь, состоящую из нескольких резисторов, подключенных параллельно.
- Резистор 1: R1 = 2 Ом
- Резистор 2: R2 = 4 Ом
- Резистор 3: R3 = 6 Ом
Общее сопротивление параллельной цепи можно рассчитать с помощью формулы:
1/R = 1/R1 + 1/R2 + 1/R3 = 1/2 Ом + 1/4 Ом + 1/6 Ом = 1/1 Ом
R = 1/(1/1 Ом) = 1 Ом
Пример 3:
Рассмотрим сложную электрическую цепь, состоящую из последовательного и параллельного соединения резисторов.
- Резистор 1: R1 = 3 Ом
- Резистор 2: R2 = 6 Ом
- Резистор 3: R3 = 2 Ом
- Резистор 4: R4 = 4 Ом
Для удобства расчетов можно сначала найти общее сопротивление для каждого параллельно соединенного участка:
Общее сопротивление для резисторов R2 и R3:
1/Rpar = 1/R2 + 1/R3 = 1/6 Ом + 1/2 Ом = 2/3 Ом
Rpar = 1/(2/3 Ом) = 3/2 Ом
Общее сопротивление для резисторов R1 и Rpar:
R = R1 + Rpar = 3 Ом + 3/2 Ом = 9/2 Ом = 4.5 Ом
Таким образом, общее сопротивление данной цепи равно 4.5 Ом.
Практические рекомендации

В процессе нахождения общего сопротивления электрической схемы могут возникать определенные сложности. В этом разделе приведены несколько полезных советов, которые помогут вам справиться с задачей более эффективно.
1. Анализируйте схему: перед тем как приступить к вычислениям, внимательно изучите схему и выделите все параллельные и последовательные соединения. Это позволит вам определить, какие законы и формулы можно применить.
2. Используйте правила соединений: помните, что при последовательном соединении сопротивления их значения складываются, а при параллельном - обратно складываются. Учтите эти правила при расчетах.
3. Обращайте внимание на сопротивление проводов: в некоторых случаях провода могут иметь существенное сопротивление, которое надо учитывать в расчетах. Особенно это актуально при работе с длинными проводами или при высоких токах.
4. Применяйте частные случаи: в некоторых случаях можно использовать известные формулы или законы для более простого расчета. Например, при работе с симметричными схемами можно использовать формулу для сопротивления резисторов в параллельном соединении.
5. Проверяйте результаты: после завершения расчетов рекомендуется проверить полученные значения общего сопротивления схемы с использованием других методов или программных средств. Это поможет избежать возможных ошибок.
Следуя этим практическим рекомендациям, вы сможете более уверенно и эффективно находить общее сопротивление электрической схемы.
Использование общего сопротивления в электротехнике
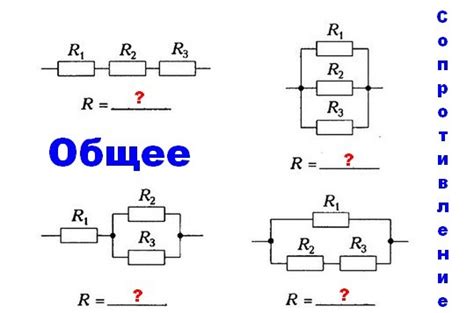
В электротехнике понятие общего сопротивления играет важную роль при расчете электрических цепей. Общее сопротивление представляет собой суммарное сопротивление, которое встречает электрический ток в цепи при его движении.
Определение общего сопротивления может быть полезно для решения различных задач, включая расчет тока, напряжения и мощности в цепях с несколькими параллельными или последовательными сопротивлениями. Чтобы найти общее сопротивление, необходимо учитывать законы Ома и рассчитывать силу тока и напряжение в различных участках цепи.
Для расчета общего сопротивления в цепи соединенных последовательно сопротивлений необходимо сложить их значения. Таким образом, если имеется ряд последовательно соединенных резисторов с сопротивлениями R1, R2, R3, ..., то общее сопротивление R обозначается как R = R1 + R2 + R3 + ...
В случае цепи, где сопротивления соединены параллельно, общее сопротивление рассчитывается по формуле:
- Вычислим обратные значения каждого сопротивления: 1/R1, 1/R2, 1/R3, ...
- Сложим обратные значения: 1/R = 1/R1 + 1/R2 + 1/R3 + ...
- Найдем общее сопротивление как обратное значение полученной суммы: R = 1/(1/R)
Зная общее сопротивление, можно рассчитать ток и напряжение в цепи с применением закона Ома (U = I * R), а также определить мощность, потребляемую цепью (P = I^2 * R).
Использование концепции общего сопротивления позволяет эффективно анализировать и проектировать сложные электрические цепи, облегчая решение задач и снижая погрешности в расчетах.