Смешанное произведение векторов – это важный математический инструмент, который находит свое применение в различных научных дисциплинах. Оно позволяет определить объем параллелограмма, построенного на трех векторах в трехмерном пространстве. Однако, как проверить корректность расчетов и достоверность полученного результата на русском языке? Давайте разберемся вместе.
Первым шагом в проверке смешанного произведения векторов является вычисление его значения. Для этого нам понадобятся координаты трех векторов и формула, которая выражает смешанное произведение через координаты. Важно обратить внимание на правильность расчетов и возможные ошибки при подстановке значений.
Понятие смешанного произведения векторов

Смешанное произведение трех векторов {a, b, c} обозначается как (a, b, c) и определяется как:
- Если векторы a, b и c образуют правую тройку, то смешанное произведение равно объему параллелепипеда, образованного этими векторами. В этом случае смешанное произведение положительно.
- Если векторы a, b и c образуют левую тройку, то смешанное произведение равно отрицательному объему параллелепипеда. В этом случае смешанное произведение отрицательно.
- Если векторы a, b и c лежат в одной плоскости или два из них совпадают, то смешанное произведение равно нулю. В этом случае параллелепипед вырождается в плоскость или отрезок.
Смешанное произведение векторов имеет много важных приложений в физике, геометрии и механике. Например, оно используется для определения площади треугольника в трехмерном пространстве, вычисления момента силы, определения объема тетраэдра и т.д.
Математические основы смешанного произведения векторов

Смешанное произведение задается следующей формулой:
(a × b) · c = det([a, b, c])
где a, b и c - трехмерные векторы, det - определитель матрицы, составленной из компонент векторов.
Свойства смешанного произведения:
- Смена порядка векторов изменяет знак результата: (b × a) · c = -(a × b) · c = (a × b) · (-c)
- Смешанное произведение равно нулю, если векторы лежат в одной плоскости или только один из них ненулевой.
- Смешанное произведение равно объему параллелепипеда, построенного на векторах a, b и c.
Смешанное произведение используется в физике, например, для определения момента силы и момента импульса. Оно также применяется в векторном анализе, геометрии и других областях математики и физики.
Формула для вычисления смешанного произведения векторов
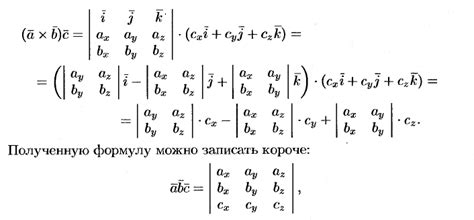
(A × B) · C = (A · C) × B
где A, B и C – это трехмерные векторы. Знак " × " обозначает векторное произведение, а " · " обозначает скалярное произведение. Вычисления проводятся в результате последовательного умножения и сложения компонент векторов.
Формула смешанного произведения векторов широко используется в различных областях, включая геометрию, физику и инженерию. Она позволяет определить объем параллелепипеда, который образуется тремя векторами.
Примеры применения смешанного произведения векторов

1. Механика: Смешанное произведение векторов используется для вычисления объёма параллелепипеда, образованного тремя векторами. Это позволяет определить объём тела, занимаемого объектом или жидкостью.
2. Электродинамика: В этой области смешанное произведение векторов применяется для расчёта магнитного потока через поверхность, ограниченную несколькими векторами. Также с его помощью можно определить момент силы, действующей на проводник в магнитном поле.
3. Геометрия: Смешанное произведение векторов используется для определения ориентации трёх точек в пространстве. Оно помогает определить, лежат ли точки на одной прямой или находятся в одной плоскости.
4. Физика: В физике смешанное произведение векторов применяется для вычисления работы, совершаемой силой при перемещении точки в трёхмерном пространстве. Также оно используется для вычисления момента импульса системы частиц.
Это лишь несколько примеров применения смешанного произведения векторов, которое находит своё применение во многих областях естественных и точных наук. Понимание и использование этого математического инструмента является важным для решения различных задач и исследований.
Свойства смешанного произведения векторов

Свойства смешанного произведения векторов:
1. Замкнутость:
Смешанное произведение векторов всегда является скалярной величиной, то есть не зависит от выбора координатной системы или базиса.
2. Антисимметричность:
Если поменять местами любые два вектора в смешанном произведении, значение останется таким же, но с противоположным знаком.
3. Линейность:
Смешанное произведение линейно относительно каждого из трех векторов. Если умножить один из векторов на скаляр, то значение смешанного произведения также умножится на этот скаляр.
4. Геометрическое значение:
Смешанное произведение векторов имеет геометрическую интерпретацию - оно равно объему параллелепипеда, построенного на этих векторах.
Таким образом, смешанное произведение векторов обладает рядом важных свойств, которые могут быть использованы при решении задач в физике, геометрии и других областях.
Практические способы проверки смешанного произведения векторов в русском языке

В математике, смешанное произведение векторов используется для определения объема параллелепипеда, образованного этими векторами. Для проверки смешанного произведения векторов, вам понадобятся знания о линейной алгебре и базовые навыки векторных операций.
Вот несколько практических способов проверки смешанного произведения векторов:
| Способ | Описание |
|---|---|
| 1 | Вычисление по формуле |
| 2 | Геометрическая интерпретация |
| 3 | Использование координатных векторов |
1. Вычисление по формуле:
Смешанное произведение векторов (A, B, C) вычисляется по следующей формуле:
(A x B) · C = Ax * (By * Cz - Bz * Cy) + Ay * (Bz * Cx - Bx * Cz) + Az * (Bx * Cy - By * Cx)
Здесь Ax, Ay, Az - координаты вектора A; Bx, By, Bz - координаты вектора B; Cx, Cy, Cz - координаты вектора C.
2. Геометрическая интерпретация:
Смешанное произведение векторов можно интерпретировать геометрически. Если объем параллелепипеда, образованного векторами A, B, C, равен нулю, то смешанное произведение векторов также будет равно нулю.
3. Использование координатных векторов:
Если векторы A, B, C заданы в виде координатных векторов, то смешанное произведение можно проверить, вычислив определитель матрицы, составленной из координатных векторов:
| Ax Ay Az |
| Bx By Bz |
| Cx Cy Cz |
Если определитель равен нулю, то смешанное произведение также будет равно нулю.
Это лишь несколько практических способов проверки смешанного произведения векторов в русском языке. В зависимости от конкретной задачи и доступных данных, можно использовать различные методы для проверки данной математической операции.