Окружность - одна из базовых и наиболее изученных в геометрии фигур. Ее длина и свойства вызывают постоянный интерес у математиков и физиков. Если вы хотите узнать, как вычислить длину окружности, образованной сечением шара, то этот материал для вас!
Формула для вычисления длины окружности известна уже более двух тысяч лет. Она была открыта в Древней Греции великими учеными Архимедом и Евклидом. Однако, чтобы применить эту формулу к сечению шара, нам потребуется некоторое знание математики.
Для начала, вспомним, что радиус окружности - это отрезок, который соединяет центр окружности с любой точкой на ней. Также важно понимать, что шар - это трехмерный объект, у которого каждой точке на поверхности соответствует свой радиус. Поэтому, для вычисления длины окружности сечения шара, нам потребуется знать радиус шара и радиус сечения.
Определение длины окружности

В математике существует формула для вычисления длины окружности. Пусть r – радиус окружности, тогда длина окружности вычисляется по формуле:
Длина = 2πr,
где π (пи) – математическая константа, примерно равная 3,14159.
Таким образом, если известен радиус окружности, можно легко вычислить ее длину. Например, если радиус равен 5 сантиметрам, то длина окружности будет:
Длина = 2π * 5 см ≈ 31,42 см.
Зная длину окружности, можно решать различные задачи связанные с геометрией, строительством, проектированием и другими областями науки и техники.
Окружность и ее свойства
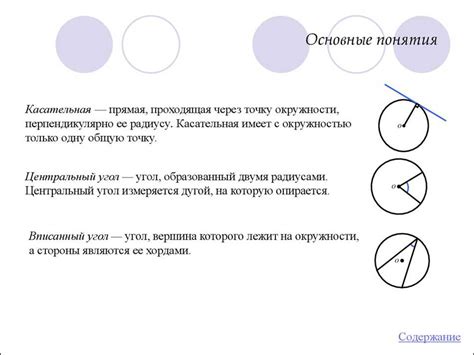
Свойства окружности:
- Диаметр окружности – отрезок, соединяющий две точки на окружности и проходящий через ее центр.
- Радиус окружности – отрезок, соединяющий центр окружности с любой точкой на ней.
- Длина окружности – периметр окружности, выражаемый по формуле L = 2πr, где L – длина окружности, а r – радиус окружности.
- Площадь круга – площадь, ограниченная окружностью. Она вычисляется по формуле S = πr^2, где S – площадь круга, а r – радиус окружности.
Длина окружности является важной характеристикой, используемой в геометрии и естественных науках. Она позволяет нам измерять расстояния по окружности, а также определять периметр и дуги на плоскости.
Зная радиус окружности, мы можем легко вычислить ее длину и использовать эту информацию для решения различных задач и проблем, связанных с окружностями.
Сечение шара и его особенности
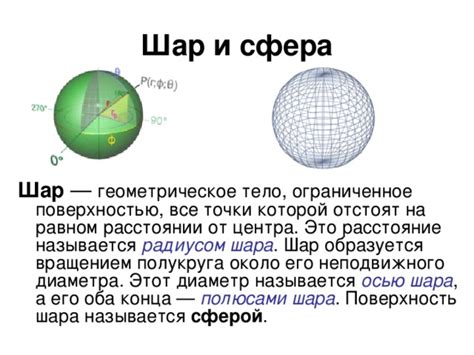
Наиболее часто встречающимся сечением шара является круглое сечение. При таком сечении плоскость проходит через центр шара, и результатом является окружность.
Для расчета длины окружности сечения шара существует специальная формула, которая учитывает радиус шара и угол, под которым плоскость пересекает шар. Формула имеет вид:
L = 2πr sin(α/2),
где L - длина окружности сечения шара, r - радиус шара и α - угол сечения.
Зная радиус шара и угол сечения, можно легко вычислить длину окружности и использовать эту информацию для решения различных задач в геометрии и математике.
Важно отметить, что при угле сечения, равном 180 градусам, сечение шара будет представлять собой плоскость, а при угле меньше 180 градусов – сферический сегмент.
Формула для вычисления длины окружности
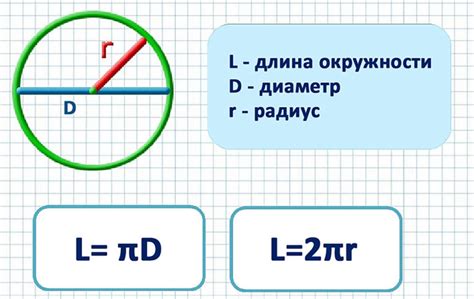
Формула для вычисления длины окружности:
C = 2πr
Где:
C – длина окружности
π – математическая константа, приблизительно равная 3,14159
r – радиус окружности
Чтобы вычислить длину окружности, необходимо умножить радиус на две, а затем умножить полученное значение на π (пи).
Например, если радиус окружности равен 5 единицам, то длина окружности будет равна:
C = 2π × 5 = 10π единиц
Таким образом, формула для вычисления длины окружности позволяет легко и эффективно определить этот параметр геометрической фигуры.
Примеры вычисления длины окружности
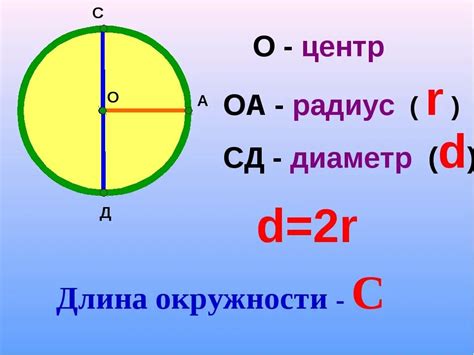
Например, рассмотрим окружность с радиусом 5 сантиметров. Для вычисления длины окружности применим формулу: C = 2πr = 2 * 3.14159 * 5 = 31.4159 сантиметров.
Если радиус окружности измеряется в метрах, то длину окружности можно вычислить по той же формуле, учитывая, что результат будет выражен в метрах.
Например, для окружности с радиусом 2 метра: C = 2πr = 2 * 3.14159 * 2 = 12.56636 метра.
Знание формулы для вычисления длины окружности позволяет производить её расчёты в различных единицах измерения и использовать в различных сферах, например при планировании строительства или изготовлении круглых предметов.
Оптимизация формулы для упрощения расчетов

Формула для вычисления длины окружности сечения шара может быть оптимизирована для упрощения расчетов. Данная формула применяется в различных областях, включая математику, физику, геометрию и инженерию. Оптимизация формулы позволяет сократить количество операций и упростить процесс расчетов.
Исходная формула для вычисления длины окружности сечения шара:
L = 2πr(1 - cos(α))
Для оптимизации формулы можно использовать следующие подходы:
- Использование альтернативных выражений для тригонометрических функций. Например, вместо cos(α) можно использовать √(1 - sin²(α)).
- Использование предварительно вычисленных значений для тригонометрических функций. Например, можно создать таблицу со значениями sin(α), cos(α) и использовать их в формуле.
- Упрощение выражений путем алгебраических преобразований. Например, можно использовать тригонометрические тождества для упрощения формулы.
Применение этих подходов позволяет сократить количество операций и упростить процесс расчетов. Оптимизированная формула может иметь вид:
L = 2πr√(2sin(α))
Таким образом, оптимизация формулы для вычисления длины окружности сечения шара позволяет существенно упростить и ускорить расчеты на практике.
Формула для вычисления длины окружности сечения шара очень полезна и применима в различных сферах жизни.
Во-первых, она широко используется в геометрии и геодезии. Зная радиус шара и угол сечения, можно очень точно вычислить длину окружности, что позволяет строить и проектировать различные объекты. Например, в строительстве используются шаровые купола и башни, и для их создания необходимо знать длину окружности сечения.
Во-вторых, данная формула применяется в физике и механике. Она позволяет вычислить длину траекторий движения шаровых объектов, что важно при моделировании и расчете движения различных тел.
Кроме того, формула имеет практическое применение в других областях, таких как архитектура, дизайн, создание упаковок и технических устройств.
Важно отметить, что для получения точных значений рекомендуется использовать большую точность в вычислениях, так как округление может привести к искажению результатов.