Призма - это геометрическое тело, образованное к трем или более вертикальным граням и двумя теми же по размеру и форме гранями, расположенными в основании. Однако, что делать, если требуется рассчитать объем призмы, у которой одно или несколько оснований отсечены? Не стоит паниковать, ведь существует специальная формула, позволяющая решить эту задачу.
Формула для расчета объема призмы с отсеченными основаниями выглядит следующим образом: V = Sh * H, где V - объем призмы, Sh - площадь основания, H - высота призмы. Однако, чтобы понять, как применить эту формулу на практике, полезно рассмотреть несколько примеров.
Пример 1: Пусть дана призма с прямоугольным основанием, у которой одно основание отсечено. Площадь верхней грани (Sh) равна 40 квадратных сантиметров, а высота (H) составляет 10 сантиметров. Для начала найдем площадь полного основания (S), умножив длину на ширину: S = 5 см * 8 см = 40 квадратных сантиметров. Теперь можем рассчитать объем, подставив все значения в формулу: V = 40 квадратных сантиметров * 10 см = 400 кубических сантиметров.
Пример 2: Рассмотрим призму с треугольным основанием, у которой одно основание отсечено. Площадь верхней грани (Sh) равна 24 квадратных метра, а высота (H) составляет 6 метров. Найдем площадь полного основания (S), используя формулу площади треугольника: S = 1/2 * a * h = 1/2 * 8 м * 6 м = 24 квадратных метра. Подставим значения в формулу для объема призмы: V = 24 квадратных метра * 6 м = 144 кубических метра.
Теперь, когда ты знаешь, как рассчитать объем призмы с отсеченной областью, ты сможешь успешно решать подобные задачи. Запомни формулу V = Sh * H и правильно подставляй значения. Удачи в изучении геометрии!
Определение отсеченной области

Для определения объема отсеченной области, необходимо знать площадь основания фигуры, ширину и высоту отсечки. Формула для расчета объема отсеченной области зависит от типа геометрической фигуры.
Например, для расчета объема отсеченной области прямоугольного параллелепипеда, необходимо умножить площадь основания на высоту отсечки:
Объем отсеченной области прямоугольного параллелепипеда = Площадь основания x Высота отсечки
Аналогично, для расчета объема отсеченной области пирамиды или призмы, необходимо умножить площадь основания на высоту отсечки и поделить результат на 3:
Объем отсеченной области пирамиды или призмы = (Площадь основания x Высота отсечки) / 3
Используя соответствующую формулу для своего случая, вы сможете легко определить объем отсеченной области нужной фигуры и использовать эту информацию при выполнении задач и решении практических задач.
Формула расчета объема призмы
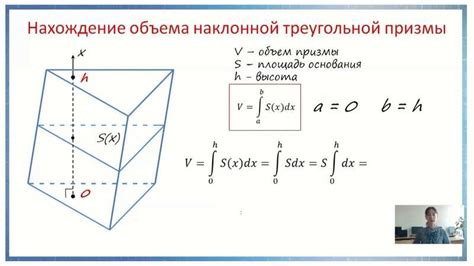
Объем призмы может быть рассчитан с помощью следующей формулы:
| Формула | Описание |
| V = S * h | Объем призмы равен произведению площади основания (S) на высоту (h). |
Где:
- V - объем призмы;
- S - площадь основания;
- h - высота.
Для расчета объема призмы, необходимо знать площадь основания и высоту. Если данные известны, достаточно перемножить их, чтобы получить объем призмы.
Например, если площадь основания составляет 5 м², а высота равна 10 метрам, то объем призмы будет:
V = 5 м² * 10 м = 50 м³
Таким образом, объем призмы составит 50 кубических метров.
Пример 1: Расчет объема призмы с отсеченной областью
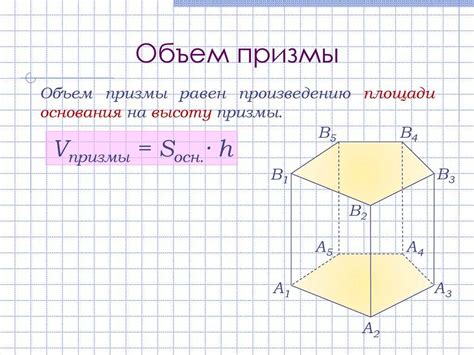
Допустим, у нас есть призма соответствующая начертанию в таблице ниже:
| Размеры | Значение |
|---|---|
| Высота призмы (h) | 10 см |
| Площадь верхней основы (S1) | 20 кв.см |
| Площадь нижней основы (S2) | 10 кв.см |
Для расчета объема такой призмы с отсеченной областью, нужно вычислить разницу между объемом призмы с общими размерами и объемом отсеченной части. Формула для расчета объема призмы с отсеченной областью выглядит так:
Объем = Высота призмы (h) * (Площадь верхней основы (S1) + Площадь нижней основы (S2) + √(Площадь верхней основы (S1) * Площадь нижней основы (S2))) / 2
Подставив значения из таблицы, получаем:
Объем = 10 см * (20 кв.см + 10 кв.см + √(20 кв.см * 10 кв.см)) / 2
Выполняя вычисления, получаем:
Объем = 10 см * (20 кв.см + 10 кв.см + √(200 кв.см2)) / 2
Объем = 10 см * (20 кв.см + 10 кв.см + 14,14 кв.см) / 2
Объем = 10 см * (44,14 кв.см) / 2
Объем = 220,7 куб.см
Таким образом, объем призмы с отсеченной областью составляет 220,7 куб.см.
Пример 2: Как рассчитать объем призмы с отсеченной пирамидальной областью
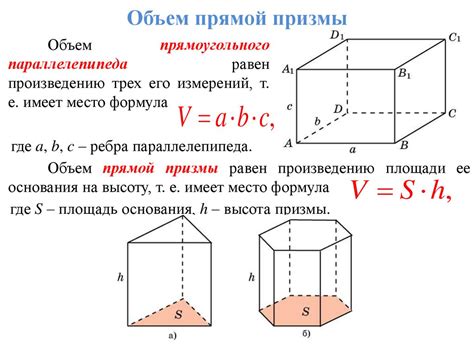
Для расчета объема такой призмы мы можем разбить ее на две части: основную часть, которая является прямоугольной призмой, и отсеченную часть, которая является пирамидой.
1. Рассчитаем объем основной части призмы. Он равен площади основания (a * b) умноженной на высоту призмы (h):
V1 = a * b * h
2. Рассчитаем объем отсеченной пирамидальной области. Он равен площади верхнего основания пирамиды (S) умноженной на высоту отсеченной области (h1) и деленной на 3:
V2 = (S * h1) / 3
3. Общий объем призмы с отсеченной пирамидальной областью равен сумме объемов основной части и отсеченной части:
V = V1 + V2
| Величина | Значение |
|---|---|
| a | 5 см |
| b | 8 см |
| h | 10 см |
| S | 16 см2 |
| h1 | 4 см |
1. Рассчитаем объем основной части призмы:
V1 = 5 см * 8 см * 10 см = 400 см3
2. Рассчитаем объем отсеченной пирамидальной области:
V2 = (16 см2 * 4 см) / 3 = 21,33 см3
3. Общий объем призмы с отсеченной пирамидальной областью:
V = 400 см3 + 21,33 см3 = 421,33 см3
Таким образом, объем призмы с отсеченной пирамидальной областью составляет 421,33 см3.
Пример 3: Как рассчитать объем призмы с отсеченными вершинами

Чтобы рассчитать объем призмы с отсеченными вершинами, необходимо знать высоту призмы (h), площадь отсеченной вершины (Abase), а также площадь основания (Atop).
Формула для расчета объема такой призмы выглядит следующим образом:
V = (h / 3) * (Abase + Atop + √(Abase * Atop))
Давайте рассмотрим пример. Предположим, у нас есть призма с высотой 6 единиц, площадью отсеченной вершины 12 единиц квадратных и площадью основания 16 единиц квадратных. Найдем объем этой призмы.
Подставим известные значения в формулу:
V = (6 / 3) * (12 + 16 + √(12 * 16))
Выполняем вычисления:
V = (2) * (12 + 16 + √(192))
V = 2 * (12 + 16 + 13.856)
V = 2 * (41.856)
V ≈ 83.712
Таким образом, объем призмы с отсеченными вершинами равен примерно 83.712 единицам кубическим.
Эта формула и методика расчета могут быть использованы для призм с различными формами отсеченных вершин.
Особые случаи: Сферическая отсеченная область
Когда рассчитывается объем отсеченной области, в которой формой служит сфера, возникают особые случаи. В таких ситуациях, вместо формулы для прямоугольной или треугольной отсеченной области, мы должны использовать формулу для сферы.
Для расчета объема сферической отсеченной области необходимо знать внешний и внутренний радиусы сферы, а также высоту отсеченного сегмента.
Формула для расчета объема сферической отсеченной области выглядит следующим образом:
V = (1/6) * π * h * (3(R_1^2 + R_2^2 + R_1*R_2) - h^2),
где V - объем отсеченной области, π - математическая константа, h - высота отсеченного сегмента, R_1 и R_2 - внутренний и внешний радиусы сферы соответственно.
Например, предположим, что у нас есть сфера с внутренним радиусом 4 м и внешним радиусом 6 м. Высота отсеченного сегмента равна 2 м. Мы можем использовать формулу для расчета объема сферической отсеченной области, чтобы найти результат.
V = (1/6) * 3.14 * 2 * (3(4^2 + 6^2 + 4*6) - 2^2)
После выполнения математических операций получаем:
V ≈ 285.71 м^3
Таким образом, объем сферической отсеченной области равен примерно 285.71 кубическому метру.
Значение и применение расчета объема призмы по отсеченной области
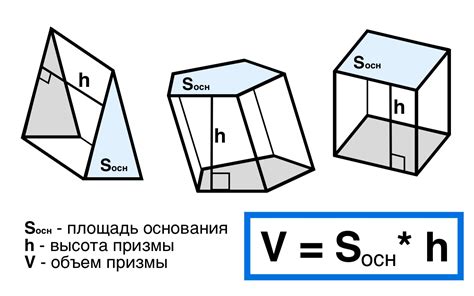
Расчет объема призмы по отсеченной области имеет большое значение в математике и геометрии. Этот расчет позволяет определить объем трехмерной фигуры, у которой вершины образуют отсеченную область двух параллельных плоскостей.
Применение данного расчета может быть найдено в различных сферах, таких как архитектура, инженерное строительство, дизайн и других областях, где требуется определить объем пространства с отсеченной формой.
Для расчета объема призмы по отсеченной области используется формула, основанная на вычислении площади сечения и длины высоты:
V = S * h
где:
- V - объем призмы;
- S - площадь отсеченной области;
- h - длина высоты призмы.
Примером применения рассчета объема призмы по отсеченной области может служить оценка объема жидкости, находящейся в резервуаре нестандартной формы, либо определение объема пустоты внутри объекта, созданного методами трехмерного моделирования.
Таким образом, расчет объема призмы по отсеченной области позволяет учесть нестандартные формы и дать более точные результаты в различных областях науки и техники.