Параллельные векторы являются основным понятием в линейной алгебре и находят широкое применение в физике, геометрии и других науках. Сложение параллельных векторов является одной из основных операций с векторами и позволяет получить новый вектор, который имеет такое же направление и противоположную или равную длину.
Для сложения параллельных векторов необходимо совместить их начала (точки приложения) и построить вектор, который их "суммирует". Если векторы имеют противоположные направления, то их сумма будет вектором нулевой длины. В случае, если векторы имеют одинаковое направление, то сумма будет равна вектору, который имеет такое же направление и равную длину.
Когда необходимо сложить несколько параллельных векторов, можно использовать метод последовательного сложения. Для этого нужно первый вектор поставить на начало второго вектора и построить новый вектор, который соединяет конец первого вектора с концом второго. После этого последовательно добавляются остальные векторы, построив новые векторы, которые соединяют концы уже сложенных векторов с началом следующих. В результате получится вектор, который является суммой всех векторов.
Векторы: как их сложить
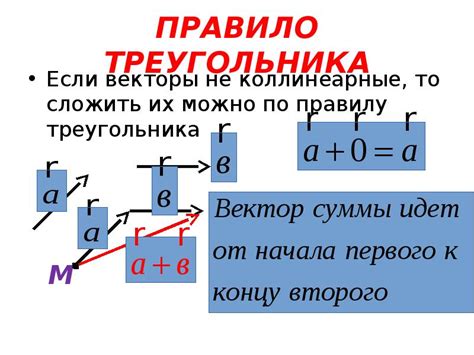
Для сложения параллельных векторов, эти векторы должны иметь одно и то же направление и быть одинаковой длины. Проще говоря, они должны быть сонаправленными и равными друг другу.
Следующие шаги помогут нам сложить параллельные векторы:
- Выравниваем векторы таким образом, чтобы их начальные точки были в одной и той же позиции.
- Прокладываем новый вектор, начинающийся в начальной точке первого вектора и заканчивающийся в конечной точке последнего вектора. Этот новый вектор будет являться их суммой.
- Измеряем длину этого нового вектора с помощью линейки или другого измерительного инструмента. Это даст нам результат сложения параллельных векторов.
Параллельные векторы могут использоваться, например, для определения силы тяжести, векторов движения или сил, действующих на объекты в физике и инженерии. При сложении параллельных векторов важно учесть их направление и равенство.
Определение вектора и его свойства

Свойства векторов:
| Свойство | Описание |
|---|---|
| Длина | Вектор имеет определенную длину, которая определяется модулем (абсолютной величиной) вектора. |
| Направление | Вектор имеет определенное направление, которое можно определить с помощью угла между вектором и некоторой базовой осью или другим вектором. |
| Противоположный вектор | Для каждого вектора существует противоположный вектор, который имеет ту же длину, но противоположное направление. |
| Сумма векторов | Сумма двух векторов определяется как вектор, который имеет направление и длину, равные сумме направлений и длин векторов-слагаемых. |
| Умножение вектора на скаляр | Умножение вектора на скаляр приводит к изменению его длины, сохраняя при этом его направление. Положительное умножение на скаляр увеличивает длину вектора, а отрицательное – уменьшает. |
Сложение векторов: основные принципы
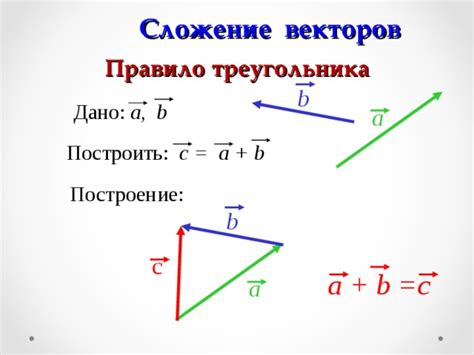
Основной принцип сложения параллельных векторов состоит в следующем: чтобы сложить два вектора, их начало должно совпадать. Затем, к концу первого вектора прилагается второй вектор, и точка, в которой они пересекаются, становится конечной точкой суммарного вектора.
Важно помнить, что сложение векторов подчиняется закону коммутативности, то есть порядок слагаемых не влияет на итоговый результат. Также стоит отметить, что результат сложения векторов имеет свои характеристики, такие как длина (модуль) и направление.
При сложении векторов необходимо учитывать их ориентацию. Если два вектора направлены в одну сторону, то итоговый вектор будет иметь такое же направление. Если же векторы направлены в противоположные стороны, то итоговый вектор будет иметь направление, противоположное первым двум.
Хорошо освоив основные принципы сложения параллельных векторов, вы сможете успешно применять их в решении задач физики, математики и других наук, связанных с векторами.
Графический метод сложения векторов

Для сложения двух параллельных векторов необходимо взять начало первого вектора и построить второй вектор от того же начала. По сути, второй вектор будет сложен с первым.
Таким образом, если мы хотим найти сумму двух векторов A и B, мы должны построить векторную диаграмму, где A будет первым вектором, а B - вторым. Результатом сложения будет вектор, проведенный от начала первого вектора до конца второго вектора.
На векторной диаграмме также можно найти длину и направление полученного вектора. Длина вектора определяется масштабом построения диаграммы, а направление - углом между исходными векторами.
Графический метод сложения векторов является наглядным способом визуализации операции сложения и часто используется в физике и математике для объяснения основных понятий векторов.
Уравнения для сложения векторов

Сложение параллельных векторов может быть выражено с помощью уравнений.
Пусть у нас есть два параллельных вектора A и B, которые направлены вдоль одной прямой. Сложение этих векторов можно записать следующим образом:
A + B = C,
где C - это вектор, полученный в результате сложения A и B.
Уравнения для сложения векторов можно записать в координатной форме. Если вектор A имеет координаты (x1, y1, z1) и вектор B имеет координаты (x2, y2, z2), то координаты вектора C будут:
xc = x1 + x2,
yc = y1 + y2,
zc = z1 + z2.
Таким образом, чтобы сложить два параллельных вектора, необходимо сложить соответствующие координаты каждого вектора.
Примеры сложения параллельных векторов
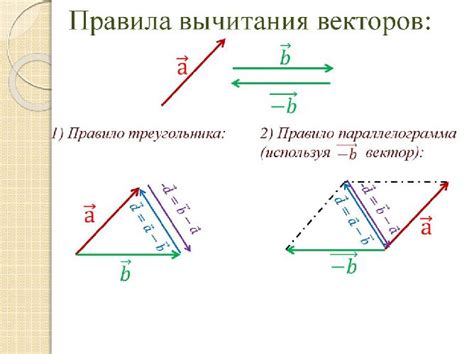
Пример 1:
Даны два параллельных вектора: вектор AB и вектор BC. У вектора AB длина 4 единицы, а у вектора BC длина 2 единицы. Чтобы сложить эти векторы, нужно просто сложить их координаты по каждой оси. В данном случае, координата x для вектора AB равна 3, а для вектора BC равна 1. Результатом сложения будет вектор AC с координатами (3+1, 0), то есть (4, 0).
Пример 2:
Даны два параллельных вектора: вектор PQ и вектор QR. У вектора PQ длина 6 единиц, а у вектора QR длина 3 единицы. Также известно, что вектор PQ направлен вправо, а вектор QR – влево. Для сложения этих векторов, нужно вычислить разность их координат по каждой оси. В данном случае, координата x для вектора PQ равна 6, а для вектора QR равна -3. Результатом сложения будет вектор PR с координатами (6+(-3), 0), то есть (3, 0).
Пример 3:
Даны три параллельных вектора: вектор UV, вектор VW и вектор WX. У всех векторов длина 5 единиц и они направлены в одну сторону. Чтобы сложить такие векторы, нужно сложить их координаты по каждой оси. В данном случае, координата x для всех векторов равна 2. Результатом сложения будет вектор UX с координатами (2+2+2, 0), то есть (6, 0).
Таким образом, сложение параллельных векторов сводится к сложению их координат по каждой оси.
Практическое применение сложения векторов
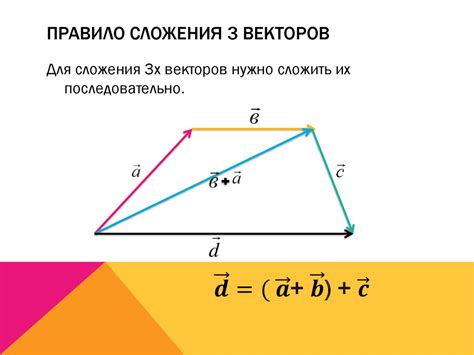
Одним из практических примеров применения сложения векторов является навигация. Например, при планировании маршрута движения корабля на море или самолета в воздухе необходимо учитывать не только направление движения, но и силу и скорость ветра. Ветер в данном случае будет представлять собой вектор, который необходимо сложить с вектором движения транспортного средства.
Еще одним примером применения сложения векторов является механика. При расчетах различных физических систем, таких как движение тела по наклонной плоскости или удар теннисного мяча, необходимо учитывать все силы, действующие на объект. Каждая из этих сил может быть представлена как вектор, и для расчетов необходимо сложить все эти векторы в соответствии с их направлением и силой.
Сложение векторов также широко применяется в графике и компьютерных играх. Например, при моделировании движения персонажа в игре необходимо учитывать множество факторов, таких как сила гравитации, сопротивление воздуха и направление движения игрока. Векторное сложение позволяет объединить все эти факторы и получить итоговый вектор движения персонажа.
Таким образом, сложение векторов имеет широкое практическое применение и играет важную роль в различных областях науки и техники. Понимание принципов данной операции позволяет решать разнообразные задачи, связанные с движением и взаимодействием объектов в пространстве.