Составление уравнения прямой – один из ключевых навыков в геометрии, который необходимо освоить в 9 классе. Зная две точки на плоскости, можно построить прямую, которая проходит через них. Для этого необходимо составить уравнение прямой, которое будет описывать ее положение относительно осей координат.
Уравнение прямой состоит из линейной алгебраической формулы, в которой каждая переменная имеет свой коэффициент. Для составления уравнения прямой по двум точкам необходимо учесть, что прямую можно задать двумя способами: угловым и каноническим.
Угловой способ состоит в использовании углового коэффициента, который определяется как отношение разности координат по оси ординат (y) к разности координат по оси абсцисс (x). На основе углового коэффициента и известных точек можно составить линейное уравнение вида y = kx + b, где k – угловой коэффициент, b – свободный член прямой.
Канонический способ состоит в использовании изначального уравнения прямой вида Ax + By + C = 0, где A, B и C – коэффициенты, определяющие прямую. Подставив значения известных точек и решив систему уравнений, можно найти нужные коэффициенты, а следовательно, и уравнение прямой.
Описание задачи на составление уравнения прямой

В геометрии существует задача о построении уравнения прямой по двум заданным точкам. Эта задача встречается в 9 классе при изучении геометрии и алгебры.
Итак, предположим, у нас есть две заданные точки на плоскости: A(x₁, y₁) и B(x₂, y₂). Наша задача - составить уравнение прямой, проходящей через эти точки.
Для начала, нам необходимо найти наклон прямой, то есть изменение координат y и x между точками. Это можно сделать с помощью следующих формул:
Наклон прямой (m) = (y₂ - y₁) / (x₂ - x₁)
Теперь, когда у нас есть наклон прямой, мы можем использовать один из двух доступных методов для составления уравнения прямой:
1. Уравнение вида y = mx + c
Мы можем использовать уравнение вида y = mx + c, где m - наклон прямой, а c - значение оси y при x = 0. Подставляем значения m и одной из заданных точек в это уравнение, получаем значение c:
y = mx + c
y₁ = m * x₁ + c
c = y₁ - m * x₁
Теперь у нас есть полное уравнение прямой, проходящей через заданные точки A и B.
2. Уравнение вида Ax + By + C = 0
Мы также можем использовать уравнение вида Ax + By + C = 0, чтобы составить уравнение прямой. Используем следующие формулы:
A = y₂ - y₁
B = x₁ - x₂
C = x₂ * y₁ - x₁ * y₂
Теперь мы можем записать уравнение прямой в виде Ax + By + C = 0, где A, B и C - коэффициенты, полученные из формул.
Оба этих метода позволяют нам составить уравнение прямой, проходящей через две заданные точки A и B. Эти уравнения могут быть использованы для решения различных задач, связанных с геометрией и алгеброй.
Начальные данные
Координаты каждой точки представляют собой пару чисел (x, y), где x - это значение абсциссы, а y - значение ординаты. Например, первая точка может быть задана координатами (x1, y1), а вторая точка - координатами (x2, y2).
Важно отметить, что координаты точек могут быть целыми или десятичными числами, положительными или отрицательными. Знание координат точек позволяет нам определить угловой коэффициент прямой и ее сдвиг по осям.
Даны две точки на плоскости
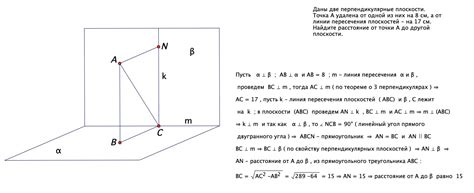
Для составления уравнения прямой, проходящей через две заданные точки на плоскости, необходимо воспользоваться формулой исходя из основного свойства прямой:
Уравнение прямой в декартовой системе координат имеет вид y = kx + b, где k - это коэффициент наклона прямой, а b - это смещение относительно оси y.
Для определения коэффициента наклона прямой (k) используется формула:
| k = (y2 - y1) / (x2 - x1) |
| где (x1, y1) и (x2, y2) - это координаты заданных точек. |
После определения коэффициента наклона (k), можно найти смещение (b) при помощи формулы:
| b = y1 - k * x1 |
Таким образом, мы можем составить уравнение прямой, проходящей через две заданные точки (x1, y1) и (x2, y2):
| y = kx + b |
Где k и b определяются с помощью формул, указанных выше.
Координаты точек
Например, точка A с координатами (2, 3) имеет абсциссу 2 и ординату 3. Точка B с координатами (-1, 5) имеет абсциссу -1 и ординату 5.
Зная координаты двух точек A(x1, y1) и B(x2, y2), мы можем найти угловой коэффициент прямой (k) с помощью формулы:
k = (y2 - y1) / (x2 - x1)
Кроме того, мы можем найти значение свободного члена (b) уравнения прямой, подставив координаты одной из точек (например, A) и значение углового коэффициента в уравнение прямой:
y - y1 = k(x - x1)
Подставляя значения координат точки A, получим уравнение прямой:
y - y1 = k(x - x1)
где k - угловой коэффициент, x1 и y1 - координаты точки A.
Понятие уравнения прямой

Для составления уравнения прямой по двум точкам необходимо знать координаты этих точек. Обозначим координаты первой точки как (x1, y1), а координаты второй точки как (x2, y2).
Для определения уравнения прямой мы будем использовать основную формулу:
y - y1 = (y2 - y1) / (x2 - x1) * (x - x1)
Где:
- y и x - переменные, представляющие координаты точки на прямой
- x1, y1 - координаты первой точки
- x2, y2 - координаты второй точки
Подставляя значения в эту формулу, мы можем получить уравнение прямой, которое будет описывать все точки на этой прямой.
Например, если первая точка имеет координаты (2, 3), а вторая точка - (5, 7), то уравнение прямой будет выглядеть следующим образом:
y - 3 = (7 - 3) / (5 - 2) * (x - 2)
Изучение уравнений прямых поможет нам не только лучше понять их свойства, но и решать задачи, связанные с геометрией, алгеброй и физикой.
Описание уравнения прямой в координатной плоскости

Чтобы составить уравнение прямой по двум точкам, необходимо знать координаты обеих точек. Пусть даны точки A(x1, y1) и B(x2, y2). Для начала найдем коэффициент наклона прямой.
Коэффициент наклона прямой k вычисляется следующим образом:
k = (y2 - y1) / (x2 - x1)
После определения коэффициента наклона k, можно найти свободный член буквы b. Для этого подставим значения координат одной из точек (например, A) и найденный коэффициент наклона в исходное уравнение, и решим его относительно b:
b = y - kx
Подставляя значения в исходное уравнение, можно получить конечный вид уравнения прямой в координатной плоскости.
Например, у нас есть точки A(2, 3) и B(4, 5), и мы хотим найти уравнение прямой. Сначала вычислим коэффициент наклона:
k = (5 - 3) / (4 - 2) = 2/2 = 1
Затем, используя этот коэффициент и координаты точки A(2, 3), найдем свободный член b:
b = 3 - 1 * 2 = 3 - 2 = 1
Таким образом, уравнение прямой будет иметь вид y = x + 1.
Отлично! Теперь вы знаете, как составить уравнение прямой в координатной плоскости, используя две точки!
Поиск наклона прямой

Для составления уравнения прямой по двум точкам необходимо определить ее наклон.
Наклон прямой можно найти, используя формулу:
m = (y2 - y1) / (x2 - x1)
где m - наклон прямой, (x1, y1) и (x2, y2) - координаты двух точек на прямой.
Если наклон прямой положительный, то прямая наклонена вправо. Если наклон отрицательный, то прямая наклонена влево. Если наклон равен нулю, то прямая горизонтальна.
Используя найденный наклон и одну из точек (x1, y1) можно записать уравнение прямой в виде:
y - y1 = m(x - x1)
где y и x - переменные, обозначающие координаты точки на прямой. Зная наклон m и координату одной точки (x1, y1), мы можем определить уравнение прямой, проходящей через эти точки.
Формула для вычисления наклона прямой через две точки

Для того чтобы составить уравнение прямой через две заданные точки, необходимо знать наклон этой прямой. Наклон прямой показывает, насколько она отклоняется от горизонтального положения.
Формула для вычисления наклона прямой между двумя точками имеет следующий вид:
| Формула: | m = (y2 - y1) / (x2 - x1) |
| Где: |
|
После вычисления наклона прямой с помощью данной формулы, можно перейти к составлению уравнения прямой в общем виде.
Определение углового коэффициента
Чтобы найти угловой коэффициент прямой, необходимо вспомнить определение наклона, который представляет собой отношение вертикального изменения и горизонтального изменения между двумя точками на прямой.
Если даны две точки (x1, y1) и (x2, y2) на прямой, то угловой коэффициент (m) прямой можно найти по формуле:
m = (y2 - y1) / (x2 - x1)
Где m - угловой коэффициент прямой, а (x1, y1) и (x2, y2) - координаты двух точек на прямой.
Знание углового коэффициента позволяет нам легко определить наклон прямой и строить ее график на координатной плоскости.
Вычисление углового коэффициента прямой

Чтобы вычислить угловой коэффициент прямой, необходимо знать координаты двух точек на этой прямой. Обозначим одну точку как (x₁, y₁), а другую как (x₂, y₂).
Угловой коэффициент прямой можно найти по формуле:
m = (y₂ - y₁) / (x₂ - x₁)
Где:
- m - угловой коэффициент прямой
- (x₁, y₁) - координаты первой точки
- (x₂, y₂) - координаты второй точки
Зная угловой коэффициент прямой, можно составить ее уравнение в виде y = mx + b, где b - свободный член.
Теперь вы можете легко вычислить угловой коэффициент прямой по двум заданным точкам и составить ее уравнение.
Поиск свободного коэффициента

Для того чтобы найти свободный коэффициент, необходимо подставить координаты одной из двух заданных точек в уравнение прямой и решить его относительно свободного коэффициента. Решение этого уравнения даст нам искомое значение свободного коэффициента.
После нахождения свободного коэффициента, мы можем записать уравнение прямой в виде y = kx + b, где k - это коэффициент наклона прямой, а b - свободный коэффициент. Таким образом, у нас есть полное уравнение прямой, которое полностью описывает ее позицию на координатной плоскости.