Графики на координатной плоскости – одна из основных тем, изучаемых в курсе информатики в 8 классе. Они являются важным инструментом для визуализации математических функций и данных. Научиться рисовать графики – значит научиться анализировать зависимости и находить решения различных задач.
Координатная плоскость – это плоская поверхность, на которой отображается график. Она состоит из двух перпендикулярных прямых – осей координат. Горизонтальная ось называется осью абсцисс, а вертикальная ось – осью ординат. Точка пересечения этих осей называется началом координат.
Чтобы нарисовать график на координатной плоскости, нужно знать уравнение соответствующей функции. Уравнение задает связь между значениями абсциссы (x) и ординаты (y). Список значений для x и соответствующие значения y позволяют построить график функции.
Основные понятия о координатной плоскости
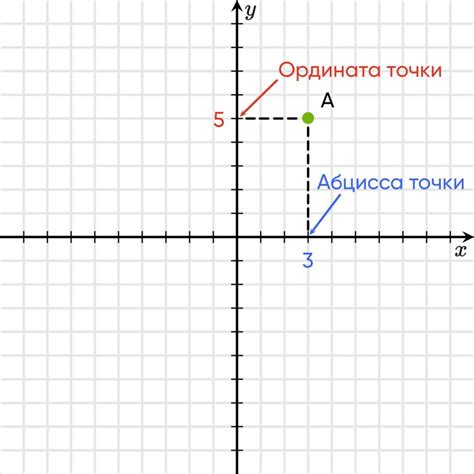
Каждая точка на координатной плоскости имеет свои координаты, которые определяются величиной разности между данной точкой и началом координат (точкой пересечения осей). Координаты точек записываются в виде упорядоченных пар чисел - (x, y), где x - значение по горизонтальной оси, y - значение по вертикальной оси.
Координатная плоскость также разделена на четыре части, называемых квадрантами. Каждый из квадрантов имеет свой знак величины координат x и y, определяющий положение точки относительно осей.
| Квадрант | Знаки координат |
|---|---|
| I | x > 0, y > 0 |
| II | x 0 |
| III | x |
| IV | x > 0, y |
На координатной плоскости также обозначены единичные отрезки, которые позволяют определить масштаб и выражать координаты точек в единицах измерения. Как правило, горизонтальная ось обозначается x, а вертикальная ось - y.
Координатная плоскость широко используется для построения и анализа графиков функций и различных геометрических фигур. На ней можно отображать данные, визуализировать информацию и решать задачи различных дисциплин, включая информатику.
Построение координатной плоскости на бумаге
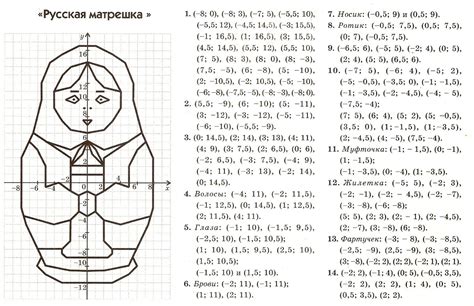
Для начала нарисуйте две перпендикулярные оси – горизонтальную ось OX и вертикальную ось OY. На пересечении этих двух осей будет находиться начало координат точка O.
Правильное масштабирование очень важно при построении графика. Оно позволит вам создавать более точные и понятные графики. Выберите шаг для делений на осях, например, 1 единица на деление. Подписывайте деления на осях начиная от точки O в обоих направлениях.
Теперь вам нужно определить точки на графике. Нарисуйте точки, соответствующие значениям вашей функции, и соедините их прямыми линиями. Не забудьте подписать график функции.
Построение графика на координатной плоскости в информатике – это интересный и важный навык. Практикуйтесь в построении графиков разных функций, чтобы лучше разобраться в этой теме.
Основные элементы графика на координатной плоскости
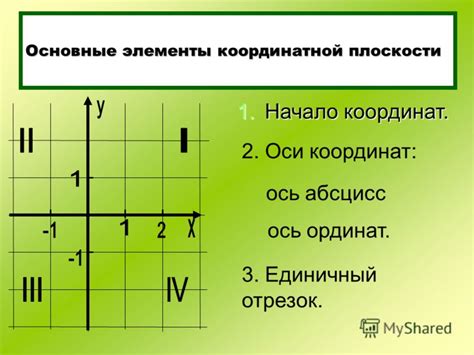
Основные элементы графика на координатной плоскости включают:
- Оси координат: вертикальная ось Y и горизонтальная ось X. Они пересекаются в точке, называемой началом координат, и делят плоскость на четыре квадранта.
- Единицы измерения: значения на осях могут быть выражены в различных единицах измерения, например, в метрах, секундах, градусах и т.д.
- Метки на осях: числа или значения, указывающие на расстояние от начала координат до определенной точки на осях. Они помогают интерпретировать данные на графике.
- Точки данных: отображение значений переменных на графике. Точки могут быть отмечены каким-либо специальным символом или цветом для отличия различных данных или категорий.
- Легенда: пояснение к графику, которое объясняет значения или категории, представленные на графике. Легенда может быть расположена в углу графика или в отдельной области.
Используя эти основные элементы, можно создавать различные типы графиков, такие как линейные, столбчатые, круговые, искусственные и другие, чтобы представить данные в наиболее наглядной и информативной форме.
Построение графика функции на координатной плоскости

Для построения графика функции на координатной плоскости необходимо определить диапазон значений аргумента, затем вычислить соответствующие значения функции. Далее с помощью точек на плоскости строится график, в котором каждая точка соответствует значению аргумента и значению функции.
Для начала, определим диапазон значений аргумента, который будет отображен на графике. Это может быть указано в условии задачи или определено на основе рассмотрения функции. Затем выбираем значения аргумента из этого диапазона с определенным шагом, например, каждый шаг может быть равен 1.
Для каждого значения аргумента вычисляем соответствующее значение функции. Если функция задана явно, то можно вычислить значение функции, подставив значение аргумента в выражение функции. Если функция задана графически или в виде таблицы значений, то можно взять значение функции из графика или таблицы для данного значения аргумента.
Полученные значения аргумента и функции образуют координаты точек на плоскости. Для каждой пары координат строится точка на плоскости. Когда все точки построены, соединяем их линиями, чтобы получить график функции на координатной плоскости.
Важно помнить, что правильное построение графика функции требует точности в выборе шага и определении диапазона значений аргумента. Также следует учесть особенности функции, например, её периодичность или область определения. Используя правильные значения и методы, можно получить точное и наглядное представление о зависимости значений функции.
Примеры задач по построению графика в информатике
Ниже приведены несколько примеров задач, в которых необходимо построить график на координатной плоскости в информатике:
Задача №1: Нарисуйте график функции y = 2x + 3 на интервале от -5 до 5.
Задача №2: Постройте график функции y = x^2 на интервале от -10 до 10.
Задача №3: Нарисуйте график функции y = sin(x) на интервале от 0 до 2π.
Задача №4: Постройте график функции y = |x + 2| на интервале от -5 до 5.
Задача №5: Нарисуйте график функции y = 1/x на интервале от -10 до 10.
В каждой задаче требуется построить график функции на заданном интервале, отметить оси координат и подписать оси и график функции. Эти задачи помогут вам лучше понять, как работать с координатной плоскостью и строить графики функций в информатике.