Высказывание – это утверждение или утвердительное предложение, имеющее значение "истина" или "ложь". Построение таблицы истинности для сложного высказывания позволяет определить все возможные комбинации истинности его составляющих частей.
Для построения таблицы истинности мы должны знать, какие операторы связывают части высказывания и как они влияют на его истинность. Наиболее распространенными операторами являются отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.
Отрицание - это оператор, меняющий истинность высказывания на противоположную. Если исходное высказывание истинно, то после применения отрицания оно станет ложным, и наоборот.
Конъюнкция, или логическое "и", объединяет два или более высказывания и истинно только тогда, когда все составляющие высказывания истинны. Если хотя бы одно из них ложно, то все высказывание становится ложным.
Таблица истинности: определение и использование
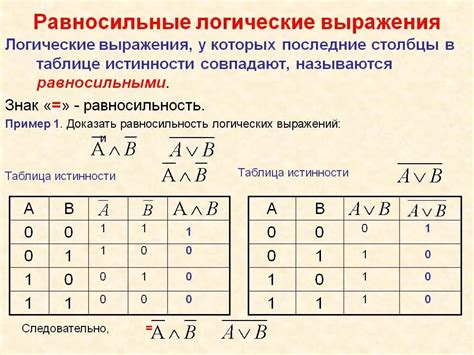
Таблица истинности состоит из заголовка и тела. В заголовке указываются все переменные, участвующие в выражении. В теле таблицы перечислены все комбинации значений переменных с соответствующими значениями истинности выражения.
Использование таблицы истинности позволяет выявить закономерности и свойства выражений, а также определить их значения в зависимости от значений переменных. С помощью таблицы истинности можно проверить, является ли выражение тождественно истинным или ложным.
Построение таблицы истинности начинается с определения количества переменных в выражении. Затем перечисляются все возможные комбинации значений переменных и вычисляются значения выражения. Истинным значениям присваивается "1", а ложным - "0".
Таблица истинности является мощным инструментом для анализа сложных логических выражений. Она позволяет выявить причинно-следственные связи, обнаружить ошибки в рассуждениях и принять обоснованные решения на основе логических законов.
| A | B | Выражение |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Основные элементы таблицы истинности
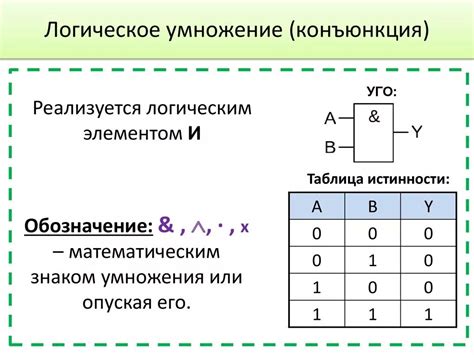
Основными элементами таблицы истинности являются:
- Высказывания - это переменные, которые могут принимать значения истины (T) или лжи (F). Каждое высказывание представляет отдельную колонку в таблице истинности.
- Комбинации значений - это все возможные комбинации значений истинности для каждого высказывания. Например, если имеется два высказывания (A и B), то возможны следующие комбинации: (T, T), (T, F), (F, T), (F, F).
- Результат - это значение истинности сложного выражения, которое строится на основе комбинаций значений для каждого высказывания. Результат представляет отдельную колонку в таблице истинности.
В таблице истинности каждая строка соответствует одной комбинации значений, а каждая колонка соответствует одному высказыванию или результату. Таким образом, таблица истинности представляет собой матрицу, где значения истинности располагаются в ячейках.
Используя таблицу истинности, можно анализировать и определять логические связи между высказываниями, а также определять значения истинности сложных выражений в зависимости от значений высказываний, что помогает в решении логических задач и принятии решений.
Построение таблицы истинности на примере простого высказывания

Для построения таблицы истинности сложного высказывания необходимо разобрать его на простые высказывания и определить все возможные комбинации значений этих высказываний. Для наглядности используется таблица, где каждая строка представляет одну комбинацию значений, а каждый столбец соответствует простому высказыванию.
Рассмотрим пример:
Пусть у нас есть два простых высказывания: "А" и "Б". Каждое высказывание может иметь два значения: истина (1) или ложь (0).
| А | Б |
|---|---|
| 0 | 0 |
| 0 | 1 |
| 1 | 0 |
| 1 | 1 |
Таким образом, получаем все возможные комбинации значений простых высказываний. Далее, для каждой комбинации нужно определить значение сложного высказывания. Для этого используются логические операции (конъюнкция, дизъюнкция, исключающее ИЛИ и т. д.), которые объединяют простые высказывания.
Например, пусть сложное высказывание "С" состоит из конъюнкции простых высказываний "А" и "Б". Значения высказывания "С" будут следующими:
| А | Б | С = А * Б |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Таким образом, мы построили таблицу истинности для простого и сложного высказывания, которая отображает все возможные комбинации значений и результаты применения логических операций.
Сложное высказывание: определение и примеры

Сложное высказывание представляет собой логическую конструкцию, состоящую из двух или более простых высказываний, объединенных логическими операторами. Эти операторы включают в себя связки "и" (/\), "или" (\/), "не" (~), "импликация" (=>) и "эквивалентность" ().
Рассмотрим примеры сложных высказываний:
| Высказывание | Оператор | Значение |
|---|---|---|
| Петя и Вася идут в кино | /\ | Истина |
| Мама или папа приготовили обед | \/ | Истина |
| Не все студенты сдали экзамен | ~ | Истина |
| Если пойдет дождь, то я возьму зонтик | => | Истина |
| Дверь открывается, только если у тебя есть ключ | Истина |
Комбинирование простых высказываний для построения сложного

При построении таблицы истинности сложного высказывания необходимо комбинировать простые высказывания с использованием логических операций. Логические операции, такие как отрицание, конъюнкция, дизъюнкция, импликация и эквивалентность, позволяют создавать новые высказывания на основе уже существующих.
Простые высказывания представляют собой утверждения, которые могут быть либо истинными, либо ложными. Например, высказывание "Солнце светит" может быть истинным, если солнце действительно светит, или ложным, если солнце закрыто облаками.
Логические операции позволяют комбинировать простые высказывания для создания сложных высказываний. Например, операция отрицания позволяет инвертировать истинность высказывания. Так, если исходное высказывание "Солнце светит" является истинным, то его отрицание "Солнце не светит" будет ложным.
Операции конъюнкции, дизъюнкции, импликации и эквивалентности позволяют комбинировать два или более высказывания в одно сложное высказывание.
Таблица истинности является графическим инструментом, позволяющим исследовать и определить истинность сложного высказывания в зависимости от истинности его составляющих. Она содержит все возможные комбинации истинности простых высказываний, а также истинность сложного высказывания, получаемого на основе этих простых высказываний и логических операций.
Построение таблицы истинности сложного высказывания

Для построения таблицы истинности сложного высказывания необходимо учесть все его составляющие, такие как логические операторы (конъюнкция, дизъюнкция, импликация и др.) и логические переменные (истинность или ложность которых требуется определить).
Таблица истинности представляет собой матрицу, в которой перечислены все возможные комбинации истинности логических переменных. Каждой комбинации соответствует значение высказывания при данной комбинации истинности переменных.
Для заполнения таблицы истинности сначала необходимо определить количество переменных в сложном высказывании, а затем составить все возможные комбинации истинности для этих переменных. После этого с помощью логических операторов можно определить значения высказывания для каждой комбинации.
Таблица истинности позволяет систематизировать информацию и логически анализировать различные высказывания. Она может быть использована для проверки правильности выражений, для доказательства утверждений и для поиска закономерностей.
| Переменная A | Переменная B | Высказывание |
|---|---|---|
| Истина | Истина | Значение высказывания при данной комбинации истинности |
| Истина | Ложь | Значение высказывания при данной комбинации истинности |
| Ложь | Истина | Значение высказывания при данной комбинации истинности |
| Ложь | Ложь | Значение высказывания при данной комбинации истинности |
Построение таблицы истинности сложного высказывания является важным инструментом в логике и математике, позволяющим разбираться в сложных логических выражениях и проводить анализ их истинности.
Применение таблицы истинности в логических операциях и решении задач
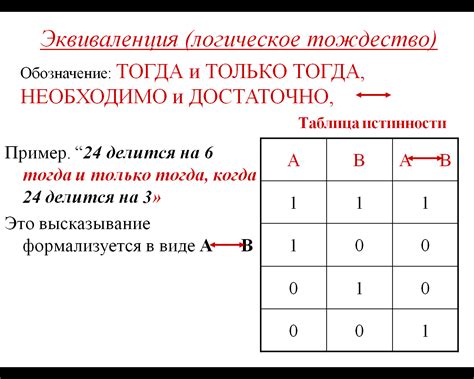
При помощи таблицы истинности можно оценить, когда составное высказывание будет истинным или ложным, в зависимости от значений истинности простых высказываний, составляющих его.
Решение задач, основанных на логических операциях, также может быть упрощено при помощи таблицы истинности. Для этого необходимо разобраться в условиях задачи, выделить простые высказывания, составить таблицу истинности для каждой логической операции и, наконец, сделать заключение на основе полученных результатов.
Примером такого решения может быть задача о поиске пропавшего кота. Предположим, у нас есть следующие простые высказывания:
- А: Кот находится в доме
- В: Кот оставил следы на полу
- С: Кота видели соседи
Используя логические операции, мы можем сформулировать составное высказывание:
Если кот оставил следы на полу ИЛИ его видели соседи, то кот находится в доме.
Составим таблицу истинности для данной задачи:
| А | В | С | А ИЛИ В | Следовательно, кот в доме? |
|---|---|---|---|---|
| Истина | Истина | Истина | Истина | Истина |
| Истина | Истина | Ложь | Истина | Истина |
| Истина | Ложь | Истина | Истина | Истина |
| Истина | Ложь | Ложь | Ложь | Ложь |
| Ложь | Истина | Истина | Истина | Истина |
| Ложь | Истина | Ложь | Истина | Истина |
| Ложь | Ложь | Истина | Ложь | Ложь |
| Ложь | Ложь | Ложь | Ложь | Ложь |
Из таблицы истинности видно, что составное высказывание верно только в том случае, если как минимум одно из простых высказываний истинно, и кот будет находиться в доме.
Таким образом, таблица истинности является полезным инструментом для анализа логических операций и решения задач, основанных на логическом мышлении. Она позволяет оценить истинность или ложность составного высказывания на основе значений истинности простых высказываний.