Степень числа – одна из основных операций в математике. Возведение в степень позволяет умножить число на себя определенное количество раз. Эта операция широко используется в различных областях, включая физику, экономику, программирование и другие.
Для возведения числа в степень вам понадобится знать основные правила и методы. В этом руководстве мы рассмотрим несколько способов выполнения этой операции и дадим вам подробные инструкции по каждому из них.
Первый способ – возведение числа в степень с использованием оператора "**" в языке программирования Python. Этот язык предоставляет удобный и простой в использовании синтаксис для математических операций. Мы покажем вам, как использовать этот оператор для получения результата возведения числа в степень.
Пример:
number = 2
exponent = 3
result = number ** exponent
В результате переменная "result" будет содержать значение 8, так как 2 в третьей степени равно 8.
Второй способ – использование встроенной функции "Math.pow()" в языке программирования JavaScript. Эта функция позволяет возвести число в указанную степень и вернуть результат. Мы покажем вам пример использования этой функции:
Пример:
var number = 2;
var exponent = 3;
var result = Math.pow(number, exponent);
В результате переменная "result" будет содержать значение 8, так как 2 в третьей степени равно 8.
В зависимости от вашего языка программирования или задачи возведения в степень, вы можете выбрать один из этих способов или использовать другие методы, предоставленные вашим языком программирования.
Основы степени числа

В математике термин "степень" обозначается с помощью знака "^" (вышестрочная стрелка) и числового показателя, указывающего степень. Например, 2^3 значит "2 в степени 3".
В основе степени числа лежит идея умножения числа на само себя заданное количество раз. Например, 2^3 можно представить как 2 * 2 * 2, что равно 8.
Показатель степени может быть как положительным, так и отрицательным числом. Положительный показатель указывает на повторное умножение числа на само себя, а отрицательный показатель - на обратную операцию, деление числа на само себя заданное количество раз.
Важно отметить, что 0 в степени 0 не имеет определенного значения. В разных математических концепциях это может быть определено по-разному или вовсе не иметь смысла.
Степень числа имеет множество приложений и используется в различных областях науки и техники. Например, степень числа может применяться для расчета вероятности, моделирования процессов роста и распада, и т. д.
В Python оператор "**" используется для возведения числа в степень. Например, 2 ** 3 возвращает результат 8.
Итак, основы степени числа состоят в повторном умножении числа на само себя заданное количество раз и обозначаются с помощью знака "^" и числового показателя. Степень числа может быть как положительным, так и отрицательным числом.
Что такое степень числа
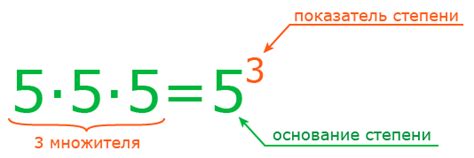
Степень числа записывается в виде an, где a - это число, а n - показатель степени.
Например, степень числа 2 возводится в виде 23, что означает умножение числа 2 на само себя три раза:
23 = 2 * 2 * 2 = 8
Таким образом, число 2 в третьей степени равно 8.
Степень числа может быть как положительной, так и отрицательной. Положительная степень означает умножение числа на себя несколько раз, а отрицательная степень - деление числа на себя несколько раз.
Как работает степень

Основание - это число, которое возводится в степень. Оно может быть любым положительным или отрицательным числом, а также нулем. Показатель степени - это целое число, которое определяет, сколько раз нужно умножить основание на само себя.
Для удобства и наглядности вычислений степени числа используются нотации и правила:
- Для обозначения степеней используется символ "^", например, "2^3" означает возвести число 2 в степень 3.
- Если степень положительная, то основание умножается на себя столько раз, сколько указано в показателе. Например, "2^3" равно 2 * 2 * 2, что равно 8.
- Если степень отрицательная, то основание возводится в обратную степень, то есть, дробится на 1 столько раз, сколько указано в показателе. Например, "2^-2" равно 1 / (2 * 2), что равно 1 / 4.
- Если показатель степени равен нулю, то результат всегда равен 1. Например, "2^0" равно 1.
Также существуют некоторые математические свойства степени, которые используются для выполнения различных операций:
- Сумма степеней: если два числа одинакового основания возводятся в степень с одинаковым показателем, то их можно сложить. Например, "2^3 + 2^3" равно "2 * 2 * 2 + 2 * 2 * 2", что равно 16.
- Разность степеней: если два числа одинакового основания возводятся в степень с одинаковым показателем, то их можно вычесть. Например, "2^4 - 2^3" равно "2 * 2 * 2 * 2 - 2 * 2 * 2", что равно 8.
- Умножение степеней: если число возводится в степень, а затем результат возводится в другую степень, то их показатели можно перемножить. Например, "(2^3)^2" равно "(2 * 2 * 2)^2", что равно 64.
- Деление степеней: если число возводится в степень, а затем результат делится на число, возводимое в другую степень, то показатели можно вычесть. Например, "(2^3) / (2^2)" равно "(2 * 2 * 2) / (2 * 2)", что равно 4.
Понимание основных правил работы со степенями поможет вам легче решать задания и применять их в практических ситуациях.
Основные понятия степени

Основные термины, связанные со степенью, включают:
| Термин | Описание |
|---|---|
| Основание | Число, которое возводится в степень. |
| Показатель степени | Число, задающее количество раз, на которое нужно умножить основание. |
| Степень | Результат операции возведения в степень. |
Обозначение степени записывается вверху у числа, и называется также "верхним индексом". Например, число 5 возводится в степень 2, записывается как 52.
Степени могут быть как положительными, так и отрицательными. В случае отрицательной степени, число становится дробным.
Возведение в степень может быть представлено в виде последовательного умножения или путем использования математической функции возведения в степень.
Как выполнять степень числа

Чтобы выполнить степень числа, нужно:
| 1 | Взять число, которое нужно возвести в степень, и записать его. Это будет основание степени. |
| 2 | Записать число, на которое нужно возвести основание степени. Это будет показатель степени. |
| 3 | Умножить основание степени само на себя столько раз, сколько указано в показателе степени. Полученное число будет результатом возведения в степень. |
Например, если нужно возвести число 2 в степень 3, то нужно умножить 2 на 2 на 2 (2 * 2 * 2) и получим результат 8.
Также стоит учитывать некоторые особенности при выполнении степени числа. Если показатель степени равен 0, то результатом всегда будет 1. Если показатель степени отрицательный, то результатом будет дробное число.
Возведение числа в степень является важной операцией в математических вычислениях и имеет много применений. Например, степень числа может использоваться для выполнения экспоненциальных функций, решения уравнений и многих других задач.
Методы выполнения степени

Существует несколько методов для выполнения степени числа:
- Использование оператора
**. - Использование функции
Math.pow(). - Использование цикла
forилиwhile.
Предлагается рассмотреть каждый из этих методов подробнее.
Использование оператора
**позволяет возвести число в определенную степень. Синтаксис:число ** степень.Пример:
let x = 2;
let result = x ** 3; // результат равен 2 * 2 * 2 = 8Использование функции
Math.pow()позволяет также возвести число в степень. Синтаксис:Math.pow(число, степень).Пример:
let x = 2;
let result = Math.pow(x, 3); // результат равен 2 * 2 * 2 = 8Использование цикла
forилиwhileпозволяет выполнить степень числа путем многократного умножения числа на себя.Пример с использованием цикла
for:let x = 2;
let exponent = 3;
let result = 1;
for (let i = 0; i < exponent; i++) {
result *= x;
}
// результат равен 2 * 2 * 2 = 8
Выбор метода выполнения степени зависит от требуемой логики программы и предпочтений разработчика.
Примеры выполнения степени

Рассмотрим несколько примеров выполнения степени числа:
- Чтобы возвести число 2 в квадрат, нужно умножить его само на себя, то есть 2 * 2 = 4.
- Для степени с отрицательным показателем, например (-3)^2, сначала нужно возвести число в квадрат, а затем полученный результат умножить на минус один: (-3)^2 = 3^2 * -1 = 9 * -1 = -9.
- При возведении числа в степень 0, результат всегда будет равен 1. Например, 5^0 = 1.
- Если число возводится в отрицательную степень, то оно должно быть представлено в виде дроби с знаменателем, равным модулю степени. Например, 2^(-3) = 1 / 2^3 = 1 / 8 = 0.125.
- При возведении числа, большего единицы, в степень, результат будет зависеть от значения степени. Например, 3^2 = 3 * 3 = 9, а 3^3 = 3 * 3 * 3 = 27.
Важно помнить, что при выполнении степени важно следовать определенным правилам и порядку выполнения операций для получения правильного результата.