Все мы знаем, что любое число, возводимое в степень, дает результат, отличный от нуля. Но что же происходит, когда ноль сам оказывается возводимым в степень? Многие поначалу удивятся, ведь обычно мы привыкли к тому, что ноль играет роль нейтрального элемента в математике. Неужели он может как-то замутить результат вычислений, подвергаясь степени? Давайте разберемся вместе!
Оказывается, вопрос "Что будет, если возвести ноль в степень?" имеет объяснение, несмотря на то, что на первый взгляд кажется, что результатом должен быть ноль. Однако, по определению, ноль возводимый в степень всегда будет равен нулю. Это связано с особенностями алгебры и доказывает, что ноль является уникальным числом.
Вы можете спросить: "Зачем вообще возможна такая операция, в которой результатом всегда будет ноль?". Ответ на этот вопрос прост: в подобных вычислениях, когда ноль возводится в степень, секретом является тот факт, что в математике можно оперировать не только числами, но и символами, описывающими их свойства и значения. Именно в таких случаях возведение нуля в степень может иметь смысл и эффект.
Оставайтесь с нами, чтобы узнать больше секретов и советов, связанных с возведением нуля в степень.
Математический феномен

Однако, по математическим конвенциям, существует некоторое исключение для нуля. Ноль возводят в положительную степень, чтобы получить ответ 0. Например, 02 = 0. Здесь ноль многократно умножается на себя, но результат будет всегда ноль.
Важно отметить, что ноль в отрицательной степени невозможно. Поэтому 0-2 или 0-1 не имеют математического значения и не имеют определенного ответа. Как говорят математики, данное выражение не определено или бесконечно.
Таким образом, математический феномен возвести ноль в степень связан с особыми правилами, которые позволяют нулю оставаться нулем при возведении в положительную степень, но не имеют значения при возведении в отрицательную степень.
Теоретическое объяснение

В математике существует специальное правило, которое говорит о том, что любое число, возведенное в степень ноль, равно единице. Это правило можно записать следующим образом:
- а0 = 1, если а ≠ 0
Однако, когда речь идет о числе ноль в степени ноль, ситуация становится несколько сложнее. Исходя из определения, ноль возводится в степень как множитель, которого нужно умножить сам с собой определенное количество раз.
При рассмотрении значения нуля в степени ноль возникает проблема – невозможно определить точное значение этого выражения. Некоторые математики считают, что результат должен быть равен единице, поскольку при умножении произвольного числа на ноль оно обращается в ноль, и чтобы сохранить свойство равенства, приходится заменять ноль на единицу и утверждать, что оно обладает свойством равенства. Другие математики, наоборот, отказываются от замены значения и аргументируют свое мнение подходом, основывающимся на анализе графика функции, где ноль возводится в степень.
Таким образом, вопрос о значении ноля в степени ноль остается спорным и не имеет однозначного решения. Исследователи и математики до сих пор не достигли консенсуса по этому вопросу, а различные математические дисциплины могут предлагать разные подходы к решению этого вопроса.
Значение и применение

Это свойство нуля в степени имеет ряд практических применений. Оно может быть полезным в различных математических и инженерных задачах. Например, в решении уравнений или в расчетах при моделировании физических систем.
Значение нуля в степени также имеет теоретическое значение в математике и является одной из основных свойств алгебры. Оно позволяет определить некоторые математические операции и системы с более точной и строгой формулировкой.
Знание и понимание свойства нуля в степени является важным элементом при изучении математики и его применении в реальных задачах.
Исторические аспекты

Вопрос о том, как возвести ноль в степень, имеет давнюю историю. Стремление человека к познанию и пониманию окружающего мира привело к поиску способов работы с математическими операциями. Знание о возведении числа в степень имеет свои истоки еще в Древней Греции и Древнем Египте.
Заслугой греческих математиков является разработка системы алгебраических символов, с помощью которых стали возможными более сложные вычисления. Один из фундаментальных математиков Древней Греции - Евклид - в своем труде "Начала" подробно описал основные правила работы с числами, включая возведение в степень.
Великий ученый Аристотель также внес свой вклад в развитие математики, изучая, в том числе, возведение чисел в натуральные степени. Египетские математики, в свою очередь, разрабатывали способы работы с арифметическими выражениями и занимались проблемой возведения в степень некоторых чисел, включая ноль.
Тем не менее, вопрос о том, как возвести ноль в степень, оставался открытым на протяжении многих веков. В течение этого времени были разработаны именно теоретические основы математики, которые необходимо знать для того, чтобы правильно работать с возведением нуля в степень.
Первые упоминания
Индийский математик из IV века, Брахмагупта, в своем труде "Брахмаспутасиддханта" упомянул, что ноль в степени равняется единице. Он сформулировал правило, согласно которому ноль в степени нуль или отрицательное число также равны единице.
В арабском мире развивались исследования нуля в степени. Математик и физик ал-Хорезми в IX веке, в своей книге "Китаб ал-Хисаб ал-Хинди" (Книга индийского счета), предложил правило, согласно которому ноль в степени равняется нулю. Он представил таблицу из пяти возведений нуля в степень, начиная с нулевой степени и заканчивая четвертой: ноль в нулевой степени равняется нулю, а остальные возведения нуля в степень давали ноль в результате.
Первые упоминания о возведении нуля в степень находятся в древних источниках, и эта тема стала предметом дискуссий и споров на протяжении многих веков. Каждое упоминание дает нам понять, что математики из разных культур стремились объяснить и вникнуть в сути этого сложного математического вопроса.
Важные открытия и открытые вопросы

Важным открытием стало математическое доказательство того, что ноль в любой степени, кроме нулевой, равен нулю. Это открытие имеет глубокое значение для различных областей науки и технологии.
Однако, возникают открытые вопросы, связанные с самим понятием "нулевая степень". Некоторые математики исследовали возможность определения значения выражения 0^0, однако пока что ни одно определение не получило всеобщего признания.
Другим важным открытием является применение нулевой степени в различных областях, таких как физика, экономика и компьютерные науки. В каждой из этих областей имеется свое своеобразное понимание и использование нулевой степени.
Возможность возведения нуля в степень исследовалась и в прикладных задачах, в частности в математическом моделировании при описании различных процессов.
Таким образом, вопрос о возведении нуля в степень является одним из важных открытых вопросов в математике, который продолжает привлекать внимание ученых и исследователей.
Формулы и алгоритмы
Возвести ноль в степень может показаться довольно простой задачей. Однако, в математике существует несколько способов подхода и формул, которые помогут нам найти правильный результат.
Одной из наиболее распространенных формул для возведения числа в степень является следующая:
| а0 | = 1 |
| 00 | = 1 |
Таким образом, результат возведения нуля в ноль равен единице.
Кроме того, существует ряд алгоритмов, которые помогают нам получить правильный результат в случае возведения нуля в степень. Один из таких алгоритмов может быть описан следующим образом:
Если степень равна нулю, то результат равен единице.
Если степень положительная, то результат равен нулю.
Если степень отрицательная, то результат является неопределенным и может быть получен с помощью предела.
Использование соответствующей формулы или алгоритма поможет нам получить правильный результат при возведении нуля в степень.
Основные формулы
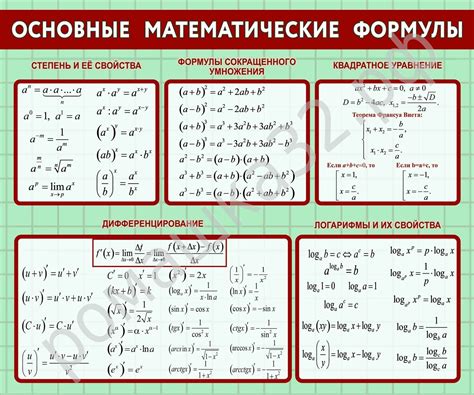
1. Возведение в степень нуля:
Правило простое: любое число, кроме нуля (a ≠ 0), возведенное в степень 0, равно 1:
a0 = 1
2. Умножение числа на ноль:
Правило также простое: умножение любого числа на ноль всегда будет равно нулю:
a * 0 = 0
3. Деление нуля на число:
В результате деления нуля на любое число (кроме самого нуля) получаем ноль:
0 / a = 0, (где a ≠ 0)
4. Любое число, кроме нуля, деленное на ноль:
Если попытаться разделить любое число (a), кроме нуля, на ноль (0), результатом будет бесконечность или неопределенность:
a / 0 = ∞, (где a ≠ 0)
или
a / 0 = не определено, (где a ≠ 0)
5. Возведение нуля в ненулевую положительную степень:
Ноль, возведенный в ненулевую положительную степень (a > 0), всегда будет равен нулю:
0a = 0, (где a > 0)
6. Возведение нуля в отрицательную степень:
При возведении нуля в отрицательную степень (a < 0), результатом будет бесконечность или неопределенность:
0a = ∞, (где a < 0)
или
0a = не определено, (где a < 0)
Запомните эти основные формулы, они помогут вам правильно решать задачи, связанные с возведением нуля в степень.
Специализированные алгоритмы

Существуют специализированные алгоритмы, разработанные для возведения нуля в степень. Они позволяют избежать математического противоречия и обеспечить корректность полученного результата.
Одним из таких алгоритмов является алгоритм нахождения нулевой степени с помощью логарифмической функции. Суть данного алгоритма заключается в следующем:
- 1. Проверяем, является ли степень равной нулю.
- 2. Если степень равна нулю, возвращаем результат равный 1.
- 3. Если степень отрицательная, меняем знак степени на положительный и выполняем далее.
- 4. Вычисляем логарифм нуля по основанию 10.
- 5. Умножаем полученный логарифм на степень.
- 6. Используя обратную функцию - экспоненту - находим число, которое равно результату умножения логарифма на степень.
- 7. Возвращаем полученный результат.
Такие специализированные алгоритмы позволяют избежать ошибок, связанных с возведением нуля в степень, и обеспечить корректность результатов. Они используются в различных математических и программных задачах, требующих возведения нуля в степень.
Практическое применение

Нуль в степени может показаться ненужным и бессмысленным, однако его практическое применение находит свое место в различных областях, особенно в математике и физике.
Например, в математике ноль в степени 0 определяется как единица, что можно использовать при вычислении некоторых сложных функций и формул. В физике нуль в степени может показывать недопустимость некоторых физических величин, а также быть ключевым показателем для определения бесконечно малых величин.
Кроме того, понимание того, как возвести ноль в степень, может помочь разобраться в основных принципах и свойствах математических операций, а также помочь развить логическое мышление и аналитические способности.