Как правильно вычислить объем окружности в цилиндре с помощью формул и примеров

Один из основных элементов, которые могут быть изучены в геометрии, - это цилиндр. Цилиндр - это трехмерная фигура, состоящая из двух круговых оснований и боковой поверхности, которая представляет собой образованную между круговыми основаниями манжету. Объем цилиндра - это объем пространства, занимаемого этим геометрическим телом. Важным элементом для определения объема цилиндра является объем его основания - окружности.

Объем окружности можно вычислить, используя простую формулу и значения радиуса. Формула для вычисления объема окружности в цилиндре представляет собой: V = π * R^2 * H, где V - объем, π - математическая константа, равная приблизительно 3,14, R - радиус основания цилиндра, H - высота цилиндра. Зная все эти значения, можно легко вычислить объем цилиндра.

Например, предположим, что у нас есть цилиндр с радиусом основания 5 м и высотой 10 м. Чтобы найти объем окружности в цилиндре, нам нужно взять значение π (приблизительно 3,14), умножить его на квадрат радиуса (5^2 = 25), а затем умножить на высоту (10). Таким образом, объем окружности в цилиндре будет равен V = 3,14 * 25 * 10 = 785 м^3.

Формула для вычисления объема цилиндра

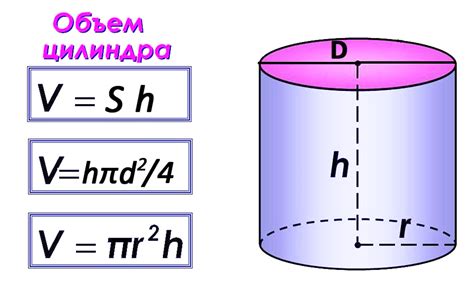
V = П * r² * h

где:

• V - объем цилиндра;
• П - число Пи, примерно равное 3,14;
• r - радиус основания цилиндра;
• h - высота цилиндра.

Чтобы вычислить объем цилиндра, необходимо умножить Пи на квадрат радиуса основания и на высоту цилиндра. Полученное число будет являться объемом цилиндра в выбранных единицах объема (например, кубических сантиметрах или кубических метрах).

Например, если радиус основания цилиндра равен 5 сантиметрам, а высота цилиндра равна 10 сантиметрам, то объем цилиндра можно вычислить следующим образом:

V = 3,14 * 5² * 10 = 3,14 * 25 * 10 = 785 сантиметров кубических.

Таким образом, объем цилиндра с радиусом основания 5 сантиметров и высотой 10 сантиметров равен 785 кубическим сантиметрам.

Как правильно вычислить объем цилиндра с помощью формулы

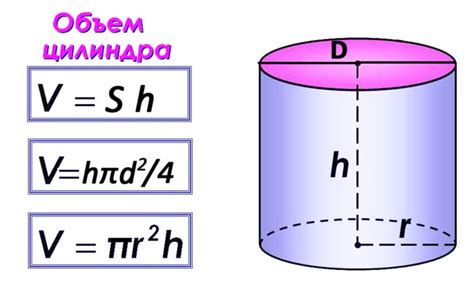
Для вычисления объема цилиндра, вам понадобятся два параметра: радиус основания (r) и высота (h). Объем цилиндра можно вычислить по формуле:

V = S * h

где V - объем цилиндра, S - площадь основания цилиндра, h - высота цилиндра.

Для вычисления площади основания цилиндра, можно использовать формулу площади круга:

S = π * r^2

где π - математическая константа, примерно равная 3.14159, r - радиус основания.

При вычислении объема цилиндра убедитесь, что все единицы измерения согласованы и выражены в одной системе измерения. Например, если радиус основания указан в сантиметрах, то и высоту цилиндра также следует указывать в сантиметрах.

Пример вычисления объема цилиндра:

1. Пусть радиус основания цилиндра равен 5 см.
2. Пусть высота цилиндра равна 10 см.
3. Рассчитаем площадь основания цилиндра:

• S = π * r^2 = 3.14159 * 5^2 = 78.53975 см^2

• V = S * h = 78.53975 * 10 = 785.3975 см^3

Теперь вы знаете, как правильно вычислить объем цилиндра с помощью формулы. Убедитесь, что ваши измерения точны и единицы измерения согласованы, чтобы получить правильные результаты.

Формула для вычисления площади окружности

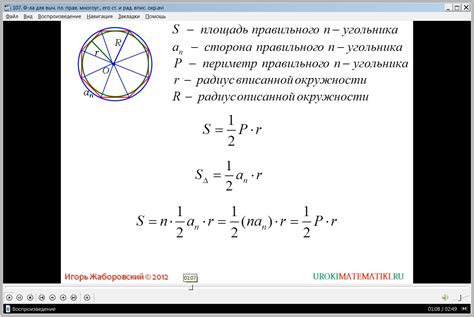
Площадь окружности можно вычислить с помощью следующей формулы:

Где:

• S - площадь окружности
• π - математическая константа, равная примерно 3,14159
• r - радиус окружности

Для того чтобы вычислить площадь окружности, необходимо знать ее радиус. Нужно возвести радиус в квадрат и умножить на π. Например, если радиус окружности равен 5, то вычисление площади будет следующим:

S = 3,14159 * 5² = 3,14159 * 25 = 78,53975

Таким образом, площадь окружности с радиусом 5 составляет примерно 78,54 единиц площади (в выбранной единице измерения).

Как правильно вычислить площадь окружности с помощью формулы

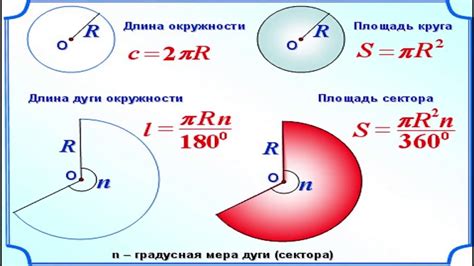
Площадь окружности можно вычислить с помощью простой математической формулы. Для этого понадобится знать радиус окружности.

Формула для вычисления площади окружности: S = π * r^2, где S - площадь окружности, π (пи) - математическая константа, примерно равная 3,14, r - радиус окружности.

Чтобы применить эту формулу, нужно знать радиус. Радиус - это расстояние от центра окружности до её края. Если неизвестен радиус, его можно вычислить, используя диаметр. Диаметр - это расстояние между двумя крайними точками окружности, проходящими через ее центр.

Пример вычисления площади окружности:

1. У вас есть окружность с радиусом 5 см.
2. Применяем формулу: S = 3,14 * 5^2.
3. Выполняем вычисления: S = 3,14 * 25.
4. Получаем ответ: S ≈ 78,5 см².

Таким образом, площадь окружности с радиусом 5 см составляет примерно 78,5 квадратных сантиметров.

Зная формулу и правильно используя ее, можно без проблем вычислять площадь окружности для разных значений радиуса. Это пригодится при решении задач в геометрии, строительстве или других областях, где требуется работать с окружностями.