Вычисление периметра и площади различных фигур может быть сложной задачей, особенно когда речь идет о сложных геометрических формах. Однако, с правильным пониманием основных принципов и некоторыми полезными советами, вы сможете легко рассчитать эти значения и применить их в реальных ситуациях.
Один из основных принципов – это разбиение сложных фигур на более простые компоненты. Например, если у вас есть фигура, состоящая из нескольких треугольников и прямоугольников, вы можете вычислить периметр и площадь каждого отдельного элемента, а затем сложить их значения, чтобы получить общий результат для всей фигуры.
Кроме того, помните о важности точности измерений. При вычислении периметра или площади, используйте точные значения сторон и углов фигуры. Если это возможно, используйте инструменты, такие как линейка или угломер, чтобы получить наиболее точные измерения.
В этой статье мы рассмотрим несколько примеров вычисления периметра и площади сложных фигур, включая комбинацию различных прямоугольников, треугольников и кругов. Вы получите практические советы и шаг за шагом примеры, которые помогут вам освоить эти навыки и применить их в будущих задачах.
Как вычислить периметр и площадь сложных фигур
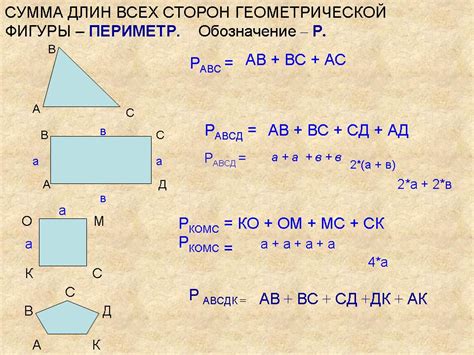
Сложные фигуры могут иметь разнообразные формы и состоять из нескольких простых геометрических фигур, таких как треугольники, прямоугольники, круги и другие. В данной статье мы рассмотрим основные методы вычисления периметра и площади таких фигур.
| Фигура | Формула периметра | Формула площади |
|---|---|---|
| Треугольник | Сумма длин всех сторон | Полупериметр, умноженный на радикаль из разности полупериметра и длин каждой стороны |
| Прямоугольник | Сумма длин всех сторон | Произведение длины и ширины |
| Круг | Двойная длина радиуса, умноженная на число π (пи) | Площадь круга равна квадрату радиуса, умноженному на число π (пи) |
Для составных фигур можно разбить их на простые фигуры, вычислить их площади и периметры, а затем сложить их результаты. Например, для вычисления площади и периметра сложной фигуры, состоящей из треугольника и прямоугольника, нужно вычислить площади и периметры каждой из простых фигур и сложить их.
Важно помнить, что для вычисления площади и периметра сложных фигур необходимо знать формулы для вычисления площадей и периметров простых фигур. Также, при использовании формул, необходимо правильно подставлять значения длин сторон или радиусов для получения корректных результатов.
Какие сложные фигуры существуют?
Ниже приведены некоторые примеры сложных фигур:
- Фракталы - это геометрические фигуры, которые обладают свойством самоподобия. Они состоят из бесконечного количества деталей, похожих на всю фигуру в целом.
- Фигуры вращения - это фигуры, получающиеся при вращении простой формы вокруг оси. Некоторые примеры включают цилиндр, конус и сферу.
- Тлин (кривая Пеано) - это фрактальная кривая, обладающая свойством самопересечения. Она представляет собой замкнутую ломаную, заполняющую плоскость.
- Мандельброт - это известный фрактал, который представляет собой комплексное число, для которого неограниченная последовательность не выходит за границы определенного радиуса.
Это лишь небольшой перечень возможных сложных фигур, которые можно найти в мире геометрии. Каждая из них обладает своими уникальными свойствами и применениями в науке и искусстве.
Как вычислить периметр прямоугольника с дыркой?
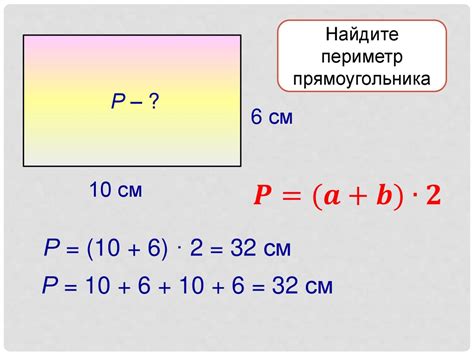
Чтобы вычислить периметр прямоугольника с дыркой, следуйте этим шагам:
- Измерьте длину внешнего прямоугольника.
- Измерьте ширину внешнего прямоугольника.
- Вычислите периметр внешнего прямоугольника, используя формулу: P = 2a + 2b, где a – длина, а b – ширина внешнего прямоугольника.
- Измерьте длину внутренней дырки прямоугольника.
- Измерьте ширину внутренней дырки прямоугольника.
- Вычислите периметр внутренней дырки прямоугольника, используя ту же формулу.
- Из всего периметра внешнего прямоугольника вычтите периметр внутренней дырки, чтобы получить периметр прямоугольника с дыркой.
Например, если длина внешнего прямоугольника равна 10, ширина – 6, длина внутренней дырки – 4 и ширина – 2, тогда:
- Периметр внешнего прямоугольника: P = 2 * 10 + 2 * 6 = 32
- Периметр внутренней дырки: P = 2 * 4 + 2 * 2 = 12
- Периметр прямоугольника с дыркой: 32 - 12 = 20
Теперь у вас есть инструкция для вычисления периметра прямоугольника с дыркой. Помните, что важно правильно измерять стороны и применять формулу для вычисления периметра. Это поможет вам точно определить периметр прямоугольника с дыркой и использовать его в дальнейших вычислениях или задачах.
Как найти площадь треугольника с основанием и высотой?
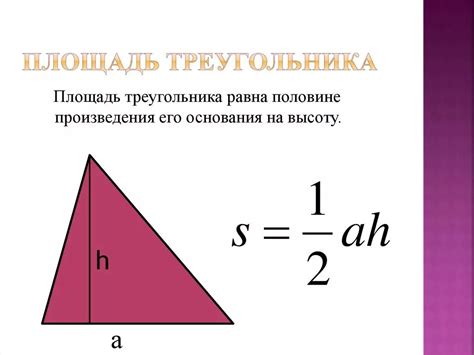
Площадь треугольника можно вычислить разными способами, в зависимости от известных параметров фигуры. Если известны длина основания и высота треугольника, то расчет площади можно выполнить по простой формуле.
Площадь треугольника равна половине произведения длины основания на высоту. Эту формулу можно записать так:
S = 1/2 * a * h
Где S - площадь треугольника, a - длина основания, h - высота треугольника.
Для примера, рассмотрим треугольник со сторонами в 5 см, 8 см и 10 см. Пусть высота этого треугольника будет 6 см. Найдем площадь треугольника по формуле:
S = 1/2 * 5 см * 6 см = 15 см2
Таким образом, площадь треугольника с основанием длиной 5 см и высотой 6 см равна 15 квадратным сантиметрам.
Обратите внимание, что единицы измерения длины основания и высоты должны быть одинаковыми - например, оба в сантиметрах или оба в метрах. Если длина основания и высоты измеряются в разных единицах, их необходимо привести к одной единице измерения перед вычислением площади.
Теперь вы знаете, как найти площадь треугольника, зная длину основания и высоту. Эта простая формула поможет вам рассчитать площадь треугольника в различных задачах и приложениях.
Как рассчитать площадь полукруга?
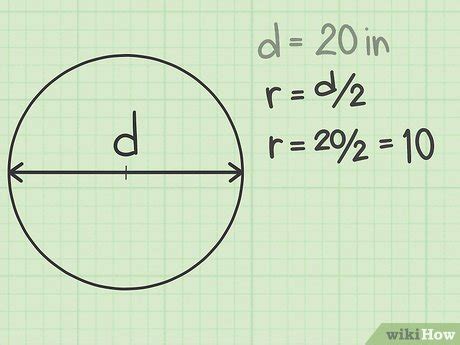
Полукруг представляет собой геометрическую фигуру, которая состоит из половины окружности и отрезка, соединяющего концы диаметра. Рассчитывая площадь полукруга, следует учитывать, что это необычная фигура и требуется специальная формула для ее определения.
Формула для нахождения площади полукруга:
Площадь полукруга равна половине площади окружности, умноженной на 2 и прибавленной к площади сегмента окружности (площадь кусочка окружности, ограниченной полукругом и отрезком).
Для расчета площади полукруга воспользуемся следующими шагами:
- Найдите длину окружности, которой принадлежит полукруг, по формуле Длина окружности = π * диаметр, где π (пи) примерно равно 3.14, а диаметр это удвоенный радиус или двойной отрезок, соединяющий концы диаметра.
- Определите площадь окружности по формуле Площадь окружности = π * радиус^2, где радиус это половина диаметра.
- Вычислите площадь сегмента окружности. Чтобы это сделать, найдите площадь треугольника, образуемого радиусом, сегментом окружности и отрезком, соединяющим концы диаметра. Площадь треугольника можно найти по формуле Площадь треугольника = (основание * высота) / 2, где основание - это длина отрезка, соединяющего концы диаметра, а высота - это перпендикулярное расстояние между основанием и серединой дуги сегмента.
- Найдите площадь полукруга, сложив площадь окружности и площадь сегмента окружности.
Используя эти шаги, вы можете рассчитать площадь полукруга и использовать ее в различных математических и инженерных задачах.
Как вычислить периметр и площадь трапеции?

Периметр трапеции равен сумме длин всех ее сторон. То есть, чтобы найти периметр, нужно сложить длины всех четырех сторон трапеции.
Площадь трапеции можно вычислить по формуле: S = (a + b) * h / 2, где a и b - длины оснований трапеции, h - высота трапеции.
Пример:
Дана трапеция с основаниями a = 5 см и b = 8 см, высота h = 6 см.
Периметр трапеции:
P = a + b + c + d = 5 + 8 + c + d
Чтобы найти длины боковых сторон c и d, нужно использовать теорему Пифагора:
c^2 = h^2 + (b - a / 2)^2
d^2 = h^2 + (b + a / 2)^2
Решив эти уравнения, можно найти значения c и d, и подставить их в формулу периметра.
Площадь трапеции:
S = (a + b) * h / 2 = (5 + 8) * 6 / 2
Результаты вычислений:
Периметр трапеции: P = 5 + 8 + c + d
Площадь трапеции: S = (5 + 8) * 6 / 2
Итак, для расчета периметра трапеции необходимо знать длины всех ее сторон, а для расчета площади - длины оснований и высоту. Используя соответствующие формулы, вы легко сможете вычислить периметр и площадь трапеции.
Как найти площадь многоугольника с помощью разбиения на треугольники?
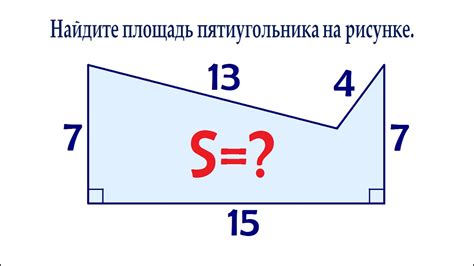
Для того чтобы выполнить разбиение, можно провести диагонали – линии, которые соединяют две вершины многоугольника, не являющиеся соседними. Количество диагоналей, которые можно провести в многоугольнике, зависит от его формы и количества вершин.
После разбиения многоугольника на треугольники, для каждого треугольника можно вычислить площадь с помощью формулы герона:
S = √(p * (p - a) * (p - b) * (p - c))
Где S – площадь треугольника, p – полупериметр (сумма длин сторон, деленная на 2), a, b, c – длины сторон треугольника.
После вычисления площадей всех треугольников, полученные значения можно сложить для получения итоговой площади многоугольника.
Метод разбиения многоугольника на треугольники позволяет достаточно точно вычислить его площадь, особенно если многоугольник имеет сложную форму или у него есть выпуклые части. Кроме того, этот метод легко реализуется при помощи компьютерных алгоритмов.