Квадрат – это геометрическая фигура, которая обладает рядом характерных свойств. Одно из них – симметрия относительно всех осей, а другое – равные стороны и углы. С точки зрения вычислений, квадрат представляет собой удобную фигуру, так как его стороны и углы равны между собой. Но как найти периметр квадрата по заданной площади?
Периметр квадрата – это сумма длин всех его сторон. Так как все стороны квадрата равны друг другу, достаточно знать длину одной из них, чтобы найти периметр. Но как найти эту длину, если известна только площадь квадрата? Для этого нужно применить ряд математических формул и алгоритмов.
Самая простая формула для нахождения периметра квадрата по заданной площади – это извлечение квадратного корня из произведения площади на 4. Другими словами, чтобы найти периметр квадрата, нужно умножить его площадь на 4 и извлечь квадратный корень из этого произведения. Таким образом, периметр квадрата равен корню квадратному из произведения площади на 4.
Что такое периметр квадрата?

Формула для вычисления периметра квадрата очень проста: P = 4 * a, где P - периметр, а - длина стороны квадрата. Таким образом, периметр квадрата равен четырем умножить на длину одной стороны.
Например, если сторона квадрата равна 5 см, то его периметр будет равен: P = 4 * 5 = 20 см.
Периметр квадрата является важной характеристикой, которая позволяет определить длину замкнутой кривой, ограничивающей квадрат. Зная периметр квадрата, мы можем также вычислить его площадь, используя формулу S = a^2, где S - площадь, а - длина стороны.
Знание понятия периметра квадрата полезно во многих сферах, например в архитектуре, геометрии, строительстве и проектировании. Вычисление периметра квадрата может помочь определить длину забора, необходимую для ограждения квадратного участка, или длину боковых сторон квадратной комнаты при расчете площади напольного покрытия.
Зачем нам нужно знать периметр квадрата?

Во-первых, знание периметра помогает определить, сколько материала нужно для обрамления квадратного предмета. Если, например, квадратное полотно нужно обтянуть рамкой, зная периметр, можно точно рассчитать необходимую длину рамки.
Во-вторых, периметр квадрата важен при планировании использования пространства. При размещении объектов на площади квадрата имеет значение длина его сторон. Зная периметр, можно точнее оценить, сколько предметов можно разместить на данной площади.
Кроме того, знание периметра квадрата может быть полезно при определении общего контура объекта. Если квадрат является частью более сложной фигуры, его периметр вместе с периметрами других фигур будет составлять общий периметр всей конструкции.
Итак, знание периметра квадрата не просто теоретическая выкладка, а конкретный инструмент для решения практических задач, связанных с измерением и планированием. Умение вычислять периметр квадрата может быть полезно во многих сферах жизни, и поможет сэкономить время и ресурсы на точных измерениях и расчетах.
Расчет периметра
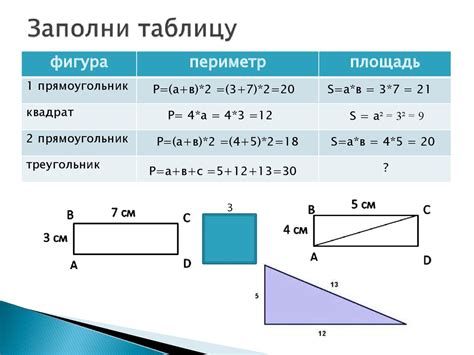
Исходя из этого, формула для расчета периметра квадрата по его площади будет следующей:
P = 4√S
Где Р - периметр квадрата, S - площадь квадрата.
Для расчета периметра квадрата по известной площади, необходимо найти квадратный корень из площади, а затем умножить полученный результат на 4.
Например, если площадь квадрата равна 16, то формула будет такой:
- √16 = 4
- 4 * 4 = 16
Таким образом, периметр квадрата с площадью 16 равен 16.
Помните, что площадь квадрата всегда является квадратом его стороны, а периметр - это сумма длин всех его сторон.
Формула для расчета периметра квадрата
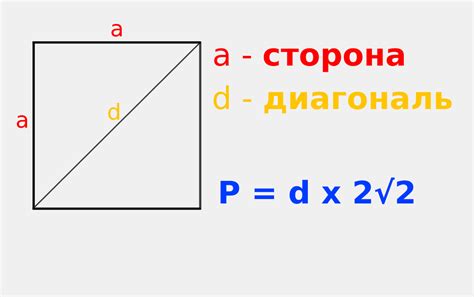
Периметр квадрата, также известного как сумма длин всех его сторон, может быть легко рассчитан с использованием простой формулы.
Если длина стороны квадрата равна а, то формула для расчета его периметра будет такой:
Периметр = 4 × а.
То есть, чтобы найти периметр квадрата по известной длине его стороны, нужно умножить эту длину на 4.
Например, если длина стороны квадрата равна 5, то его периметр будет равен:
Периметр = 4 × 5 = 20.
Примеры решения

Рассмотрим несколько примеров решения задачи по нахождению периметра квадрата по известной площади.
Пример 1:
Известно, что площадь квадрата равна 16 квадратным единицам. Найдем его периметр:
Для начала найдем длину стороны квадрата по формуле сторона = √площадь. В данном случае получаем сторона = √16 = 4.
Теперь умножим длину стороны на 4, чтобы найти периметр квадрата: периметр = 4 * сторона = 4 * 4 = 16.
Таким образом, периметр квадрата с площадью 16 квадратных единиц равен 16 единицам.
Пример 2:
Пусть площадь квадрата равна 25 квадратным единицам. Найдем его периметр:
Аналогично предыдущему примеру, найдем длину стороны квадрата: сторона = √25 = 5. Затем умножим длину стороны на 4: периметр = 4 * сторона = 4 * 5 = 20.
Таким образом, периметр квадрата с площадью 25 квадратных единиц равен 20 единицам.
Пример 3:
Допустим, площадь квадрата равна 36 квадратным единицам. Найдем его периметр:
По аналогии с предыдущими примерами, найдем длину стороны квадрата: сторона = √36 = 6. Затем умножим длину стороны на 4: периметр = 4 * сторона = 4 * 6 = 24.
Таким образом, периметр квадрата с площадью 36 квадратных единиц равен 24 единицам.
Пример 1: Расчет периметра квадрата с заданной площадью
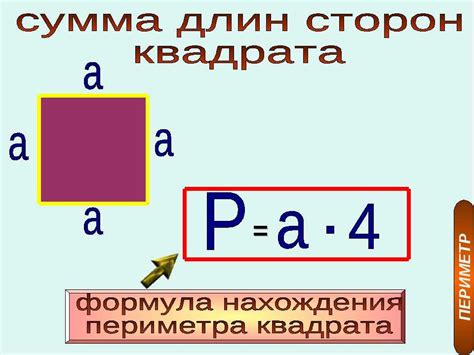
Допустим, у нас есть квадрат со стороной a и известной площадью S. Мы хотим найти периметр этого квадрата. Периметр квадрата можно найти, зная его сторону, так как все стороны квадрата равны.
Формула для нахождения периметра квадрата: P = 4a.
Если нам известна площадь квадрата (S), мы можем найти его сторону (a) с помощью формулы стороны квадрата: a = √S.
Таким образом, чтобы найти периметр квадрата с заданной площадью, мы сначала найдем сторону квадрата по формуле a = √S, а затем подставим полученное значение в формулу периметра: P = 4a.
Давайте рассмотрим пример. Предположим, что у нас есть квадрат с площадью 25 квадратных единиц. Чтобы найти его периметр, мы сначала найдем сторону квадрата: a = √25 = 5 единиц. Затем мы подставим это значение в формулу периметра: P = 4 * 5 = 20 единиц.
Таким образом, периметр квадрата со стороной 5 единиц и площадью 25 квадратных единиц равен 20 единицам.
Пример 2: Расчет периметра квадрата по заданной длине стороны
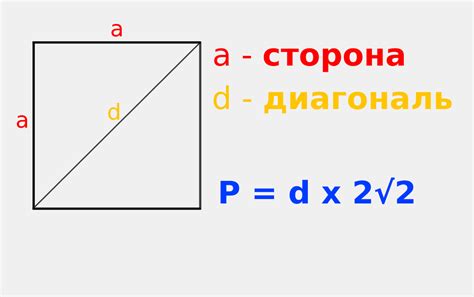
Пусть нам известна длина одной стороны квадрата, например, 5 см. Чтобы найти периметр квадрата, нужно просто умножить длину стороны на 4, так как все стороны квадрата равны.
Таким образом, чтобы найти периметр квадрата с длиной стороны 5 см, нужно выполнить следующий расчет:
- Умножить длину стороны на 4 (5 см * 4).
- Получить результат - периметр квадрата (20 см).
Таким образом, периметр квадрата с длиной стороны 5 см равен 20 см.
Этот метод можно применять для расчета периметра квадратов с любой длиной стороны. Просто умножьте длину стороны на 4 и получите результат - периметр квадрата.