Вычисление значения математического выражения может быть сложной задачей, особенно для тех, кто не имеет достаточного опыта в области математики. Однако, с некоторыми тайными трюками и советами, вы можете легко освоить эту навык и стать настоящим мастером математики!
Первым и самым важным советом для вычисления математического выражения является понимание порядка операций. В математике существует определенная иерархия операций, которую следует соблюдать при вычислении выражения. Например, скобки имеют самый высокий приоритет и должны быть решены первыми, а затем умножение и деление, а в конце сложение и вычитание. Чтение и понимание выражения по частям поможет вам структурировать вычисления и избежать ошибок.
Еще одним полезным советом является использование правил арифметики и свойств чисел для упрощения выражений. Некоторые выражения можно упростить, используя коммутативность или ассоциативность операций. Например, можно менять местами числа при сложении или умножении, или группировать числа по разным операциям. Это может существенно упростить вычисления и сделать задачу более легкой.
Не забывайте, что важно быть внимательным при выполнении математических операций. Опечатки или небрежность могут привести к неверному результату. Проверьте каждый шаг вычисления, используя калькулятор или ручные вычисления. Если вы получите разные значения, вернитесь к предыдущему шагу и убедитесь, что вы не допустили ошибку.
Следуя этим советам и тайным трюкам, вы сможете легко вычислять значения математических выражений и успешно справляться с любыми математическими заданиями. Практика и упорство – вот ключи к успеху в мире математики!
Математические выражения: как вычислить значение
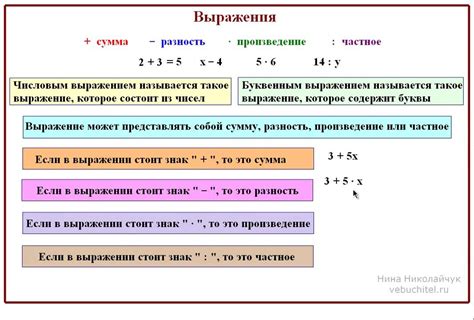
Существует несколько основных правил и методов, которые помогут вам вычислить значение математического выражения:
- Сначала решите все операции внутри скобок. Выполните операции внутри самых внутренних скобок сначала, затем двигайтесь внутрь к внешним скобкам.
- Выполняйте операции умножения и деления слева направо.
- Выполняйте операции сложения и вычитания слева направо.
- Если в выражении есть операторы с одинаковым приоритетом (например, сложение и вычитание), выполните их в порядке, в котором они появляются.
- Замените переменные на известные значения, если это возможно.
Важно помнить о приоритете операций. Умножение и деление имеют более высокий приоритет, чем сложение и вычитание.
Также стоит отметить, что вычисление математических выражений может быть упрощено с использованием специализированных программ и калькуляторов. Они могут автоматически вычислять значения выражений с высокой точностью и скоростью.
Учитесь считать с детства

Считать с детства можно с помощью различных игр и заданий, которые развивают логическое мышление и усиливают память. Детям нравятся игры, которые не только увлекут их, но и помогут им научиться считать. Это может быть игра в арифметические действия, где нужно посчитать количество фруктов или игра с использованием таблицы умножения.
Еще один способ научить детей считать - использовать различные счетные палочки, блоки или игрушки. С помощью них можно проводить различные упражнения, когда ребенок будет считать количество предметов или сложать и вычитать числа.
Но самым важным в этом процессе является постоянное общение с ребенком и постоянное повторение материала. Необходимо находить интересные и увлекательные методики, чтобы привлечь внимание ребенка и сделать процесс обучения приятным.
Еще одним полезным инструментом будут различные учебники и пособия, которые помогут детям понять и освоить основные математические понятия. Важно, чтобы учебники были интересными и доступными для восприятия, чтобы ребенок с удовольствием занимался математикой.
Учитесь считать с детства - это ключ к успеху в будущем. Развивайте математические навыки своего ребенка и помогите ему освоить этот важный предмет. Ведь, умение считать поможет ему не только в учебе, но и в жизни.
Основные математические операции

В математике существуют четыре основные операции:
- Сложение (+) – это операция, позволяющая складывать два или более числа. Например, 2 + 3 = 5.
- Вычитание (-) – это операция, позволяющая находить разность между двумя числами. Например, 5 - 3 = 2.
- Умножение (*) – это операция, позволяющая находить произведение двух или более чисел. Например, 2 * 3 = 6.
- Деление (/) – это операция, позволяющая находить частное двух чисел. Например, 6 / 3 = 2.
Кроме того, в математике используются и другие операции, такие как возведение в степень и извлечение корня. Эти операции позволяют выполнять более сложные вычисления и решать более сложные задачи.
Приоритет операций: важные правила

1. Скобки во главе
Первое правило приоритета операций - скобки. Выражение, находящееся внутри скобок, всегда выполняется первым. Важно правильно определить, какие части выражения находятся внутри скобок, чтобы вычисление происходило корректно.
2. Умножение и деление следом
После скобок выполняются операции умножения и деления. Они имеют одинаковый приоритет и выполняются слева направо. Важно учесть, что деление на ноль недопустимо.
3. Сложение и вычитание последние
После выполнения операций умножения и деления, выполняются операции сложения и вычитания. Они также имеют одинаковый приоритет и выполняются слева направо.
4. Выполнение слева направо
Если в выражении нет скобок, операции выполняются слева направо в соответствии с описанными выше правилами.
5. Использование оператора возведения в степень
Оператор возведения в степень имеет более высокий приоритет, чем умножение, деление, сложение или вычитание. Он выполняется перед всеми остальными операциями.
6. Использование специальных функций
При использовании специальных функций, таких как тригонометрические или логарифмические функции, их выполнение происходит после всех остальных операций.
Правильное понимание и применение приоритета операций - важный навык в математике и программировании. Следуя вышеуказанным правилам, можно вычислить значение математического выражения с высокой точностью и избежать ошибок.
Используйте скобки для ясности

При вычислении математического выражения может возникнуть ситуация, когда порядок выполнения операций становится неоднозначным. Для того чтобы избежать путаницы и установить ясность в порядке вычислений, рекомендуется использовать скобки.
Скобки позволяют группировать операции и указывать явный порядок выполнения действий. Важно помнить, что операции внутри скобок выполняются первыми, а затем уже производятся остальные операции в порядке, определенном приоритетом операций.
Приведем пример:
| Выражение без скобок | Результат |
|---|---|
| 4 + 2 * 3 | 10 |
| (4 + 2) * 3 | 18 |
В первом случае операция умножения выполнится первой, а затем будет произведено сложение. Во втором случае скобки группируют операцию сложения, которая выполняется первой, а затем умножение.
Использование скобок позволяет вам быть уверенным в том, как именно будут вычислены значения в вашем математическом выражении. Не стесняйтесь добавлять скобки, особенно если ваше выражение содержит множество операций разного приоритета или если оно может вызвать путаницу.
Отрицательные числа: не забывайте о знаках
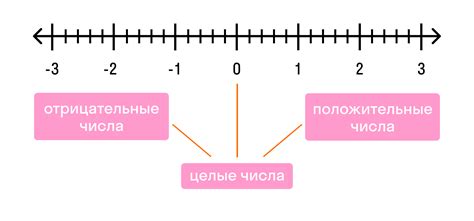
Для правильного определения знака результата необходимо учитывать следующие правила:
- При сложении отрицательного и положительного чисел необходимо вычитать по модулю и сохранять знак числа с большим модулем.
- При вычитании отрицательных чисел аналогично складыванию нужно вычитать по модулю и сохранять знак числа с большим модулем.
- При сложении (вычитании) положительного и отрицательного чисел необходимо прибавить (вычесть) и сохранить знак числа с большим модулем.
- При умножении двух чисел со знаком надо сохранить знак минус, если у чисел есть одинаковые знаки, иначе результат будет положительным.
- При делении двух чисел со знаком результат будет отрицательным, если у чисел разные знаки, иначе результат будет положительным.
Знание этих простых правил позволит избежать распространенных ошибок и получить верный результат при вычислении математических выражений, содержащих отрицательные числа.
Десятичные дроби: работаем с десятичными знаками

Десятичная дробь состоит из целой части, десятичной запятой и дробной части. Десятичная запятая отделяет целую и дробную части и обычно обозначается символом "." или ",".
Правильное использование десятичных знаков позволяет получить точные результаты при вычислении десятичных выражений. Важно помнить следующие правила:
- Позиция десятичной запятой: При работе с десятичными числами необходимо всегда учитывать позицию десятичной запятой. Она указывает, где находится разделитель целой и дробной части числа.
- Округление: При необходимости округления десятичных чисел следует придерживаться определенных правил, например, округлять вниз или вверх в зависимости от требуемой точности.
- Арифметические операции: При выполнении арифметических операций с десятичными дробями необходимо учитывать различные позиции дробных знаков и правильно располагать запятые в результате вычислений.
- Точность и округление в вычислениях: Правильное управление десятичными знаками позволит получить более точные результаты вычислений и избежать погрешностей.
Работа с десятичными дробями требует внимания и аккуратности. Следуя правилам и правильно управляя десятичными знаками, вы сможете точно вычислять значения математических выражений с десятичными числами.
Упрощение сложных выражений

Вычисление сложных математических выражений может быть непростой задачей, особенно если они содержат множество операций и переменных.
Однако, существует несколько фундаментальных правил, которые помогут вам упростить сложное выражение:
- Изучите приоритет операций: умножение и деление выполняются перед сложением и вычитанием. Выражения в скобках всегда вычисляются первыми.
- Упрощайте выражение, выполняя операции с одинаковыми знаками: сложение и вычитание, умножение и деление.
- Выполняйте вычисления по очереди, двигаясь слева направо: вычисляйте первые операции, затем вторые и так далее.
- Используйте свойства операций для упрощения выражения, например, ассоциативность и коммутативность сложения и умножения.
- Заменяйте сложные выражения их эквивалентными формами или подставляйте известные значения переменных.
Не забывайте использовать круглые скобки, чтобы явно указывать порядок операций. Если вы запутались или не уверены в правильности вычисления, вы всегда можете воспользоваться калькулятором или программой для символьных вычислений.
Упрощение сложных выражений требует практики и опыта. Постепенно разбирайтесь с правилами и проводите больше времени на решение задач, чтобы улучшить свои навыки. Следуя этим советам, вы сможете более эффективно вычислять сложные математические выражения.
Советы по решению математических задач

1. Понимание задачи
Перед тем, как приступить к решению математической задачи, важно полностью понять условие. Прочитайте задачу внимательно несколько раз, выделите ключевые слова и определите, что от вас требуется.
2. Построение плана решения
Определите пошаговый план решения задачи. Разбейте ее на более мелкие подзадачи и определите необходимые формулы, методы и инструменты для решения каждой из них.
3. Использование подходящих формул и методов
Определите, какую формулу или метод следует применить для решения задачи. Если необходимо, обратитесь к своим учебникам или другим источникам информации, чтобы найти подходящие математические формулы и методы.
4. Работа с величинами и единицами измерения
Обратите внимание на единицы измерения, представленные в задаче, и убедитесь, что все величины согласованы между собой. При необходимости, выполните все конверсии единиц измерения в одну систему.
5. Проверка ответа
После получения ответа не забудьте проверить его на соответствие условия задачи. Подставьте полученные значения обратно в задачу и убедитесь, что они подтверждают правильность решения.
Следуя этим советам, вы сможете улучшить свои навыки решения математических задач и достичь больших успехов в этой области.
Использование калькуляторов и программ
Сегодня существует множество калькуляторов и программ, которые помогают вычислять математические выражения. Они предоставляют широкий набор функций, позволяющих работать с различными типами данных и операциями.
Одним из самых популярных калькуляторов является обычный настольный калькулятор. Он позволяет выполнять базовые арифметические операции, такие как сложение, вычитание, умножение и деление. Некоторые калькуляторы также имеют возможность вычисления квадратных корней, степеней и других математических функций.
Кроме настольных калькуляторов, существуют также программы-калькуляторы для персональных компьютеров и мобильных устройств. Они обычно предоставляют дополнительные возможности, такие как работа с переменными, сохранение истории вычислений, решение уравнений и интегрирование.
Некоторые программы даже предоставляют возможность создания и выполнения сложных математических выражений с применением функций и переменных. Они достаточно гибки и удобны в использовании, особенно для решения сложных задач, требующих вычислений.
Выбор калькулятора или программы для вычисления математических выражений зависит от конкретных потребностей и предпочтений пользователя. Некоторые предпочитают простые и легкие в использовании калькуляторы, а другие предпочитают более продвинутые программы с большим набором функций. Важно выбрать такой инструмент, который наилучшим образом соответствует вашим потребностям и поможет вам справиться с задачами быстро и эффективно.