Синус - одна из основных тригонометрических функций, широко применяемых в математике и физике. Знание градусной меры синуса позволяет решать различные задачи, связанные с углами и треугольниками. Но часто бывает необходимо найти приближенное значение синуса для угла, который не представлен в таблицах. В таких случаях можно использовать приближенный метод.
Приближенный метод для нахождения градусной меры синуса основан на использовании разложения функции по степеням x. Разложение позволяет приближенно вычислить значение функции для угла любой величины, не ограничиваясь только углами, представленными в таблицах синусов.
Приближенный метод нахождения синуса основан на следующих шагах:
- Переведите градусную меру угла в радианы.
- Выберите метод, с помощью которого будет производиться приближенное вычисление: ряд Тейлора, метод Ньютона или другой.
- Вычислите приближенное значение синуса для данного угла, используя выбранный метод.
- Если необходимо, проверьте полученный результат, сравнив его с точным значением синуса, полученным из таблицы.
Используя описанный приближенный метод, можно определить градусную меру синуса для любого угла с любой точностью. Этот метод является очень полезным, особенно в случаях, когда точные значения синусов для нужных углов отсутствуют. Приближенное значение синуса позволяет решить множество математических и физических задач и упрощает процесс решения.
Что такое градусная мера синуса
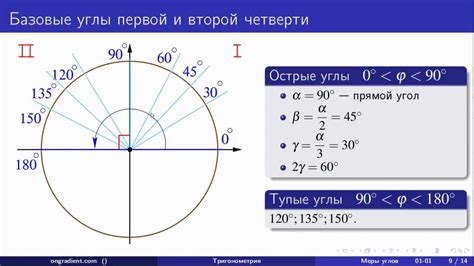
Для измерения угла в градусах с использованием синуса применяется градусная шкала, которая делится на 360 равных частей. Величина синуса угла определяется длиной противолежащего катета и гипотенузы и указывает на соотношение между ними.
Градусная мера синуса играет важную роль в математике и физике. Она используется для решения задач, связанных с геометрией, тригонометрией, механикой, астрономией и другими областями науки и техники. Знание градусной меры синуса позволяет рассчитывать углы и проводить анализ треугольников и других фигур с помощью свойств и формул, связанных с синусом.
| Градус m | Синус (sin(m)) |
|---|---|
| 0 | 0 |
| 30 | 0.5 |
| 45 | 0.7071 |
| 60 | 0.866 |
| 90 | 1 |
Таблица показывает значения синуса для некоторых углов в градусах. Эти значения используются для приближенного определения синуса углов, которые не включены в таблицу.
Описание приближенного метода

Приближенный метод нахождения градусной меры синуса основан на использовании ряда Тейлора для синуса и оценке точности приближения. Этот метод позволяет найти приближенное значение синуса с заданной точностью.
Ряд Тейлора для синуса имеет вид:
- sin(x) ≈ x - (x^3/3!) + (x^5/5!) - (x^7/7!) + ...
Для конкретного значения x, мы можем использовать этот ряд Тейлора для оценки значения sin(x). Однако, чтобы получить более точное приближение, мы должны использовать только некоторое количество членов этого ряда.
Чтобы определить количество членов, которые нужно использовать, чтобы достичь желаемой точности, можно рассмотреть остаточный член ряда. Остаточный член можно оценить с помощью формулы:
- Rn(x) ≤ |(x^(2n+1)/(2n+1)!)|
Где n - количество членов ряда, x - значение для которого нужно найти синус.
Чтобы достичь заданной точности ε, необходимо выбрать такое n, чтобы выполнить условие:
- |Rn(x)| ≤ ε
Таким образом, приближенное значение синуса можно получить, используя формулу:
- sin(x) ≈ x - (x^3/3!) + (x^5/5!) - ... + (-1)^n * (x^(2n+1)/(2n+1)!)
Где n - количество членов ряда, достаточное для достижения заданной точности.
Такой приближенный метод нахождения градусной меры синуса позволяет получить результат с желаемой точностью, используя ряд Тейлора.
Определение приближенного метода нахождения градусной меры синуса

Приближенный метод нахождения градусной меры синуса позволяет получить приближенное значение синуса для заданного угла без использования сложных математических вычислений. Такой метод основан на разложении синуса в бесконечное число слагаемых и использовании только первых нескольких из них.
Одним из удобных приближенных методов нахождения градусной меры синуса является использование ряда Тейлора. Этот ряд представляет собой бесконечную сумму слагаемых, выражающихся через производные функции. Разложение синуса в ряд Тейлора позволяет приближенно вычислить значение синуса для заданного угла.
Для использования приближенного метода нахождения градусной меры синуса необходимо знать значения первых нескольких слагаемых ряда Тейлора для синуса и последовательно складывать их для получения приближенного значения синуса.
Важно отметить, что приближенный метод нахождения градусной меры синуса дает только приближенное значение синуса и может иметь погрешность. Для получения более точных значений синуса следует использовать другие методы, такие как таблицы значений синуса или математические формулы.
Пример вычисления

Допустим, нам нужно найти приближенное значение градусной меры синуса угла 30°.
Мы можем воспользоваться таблицей приближенных значений синуса из учебника:
| Угол (градусы) | Синус |
|---|---|
| 0° | 0 |
| 10° | 0.1745 |
| 20° | 0.3420 |
| 30° | 0.5000 |
| 40° | 0.6428 |
| 50° | 0.7660 |
Из таблицы видно, что синус угла 30° равен 0.5000.
Однако, если нам необходимо получить более точное значение, мы можем воспользоваться рядом Тейлора для синуса:
sin(x) = x - (x^3)/3! + (x^5)/5! - (x^7)/7! + ...
Приближенное значение синуса угла 30° можно найти, используя первые несколько членов ряда:
sin(30°) = 30 - (30^3)/3! + (30^5)/5! - (30^7)/7! + ...
Подставляя значения и вычисляя их, мы получим приближенное значение синуса угла 30°.
Шаги вычисления градусной меры синуса

Шаг 1: Задайте угол в градусах, для которого вы хотите найти синус.
Шаг 2: Переведите градусы в радианы, умножив значение угла на π/180.
Шаг 3: Разложите значение угла в радианах в ряд Тейлора (бесконечную сумму) с точным значением синуса. Ряд Тейлора для синуса имеет вид:
sin(x) = x - (x^3/3!) + (x^5/5!) - (x^7/7!) + ...
Шаг 4: Примените приближенный метод ряда Тейлора, ограничив его конечным числом членов, чтобы получить приближенное значение синуса.
Шаг 5: Проверьте полученное приближенное значение синуса с помощью таблицы значений синуса, чтобы убедиться в его точности.
Преимущества и недостатки

При использовании приближенного метода для нахождения градусной меры синуса существуют как преимущества, так и недостатки:
- Преимущества:
- 1. Простота и доступность метода. Приближенный метод позволяет быстро вычислить приближенное значение синуса без необходимости использования сложных математических операций.
- 2. Малое количество вычислений. Применение приближенного метода требует меньшего количества вычислений, чем точный метод, что ускоряет процесс получения результата.
- 3. Адаптивность к различным ситуациям. Приближенный метод позволяет быстро находить приближенное значение синуса для любого угла без необходимости знать точное значение.
- Недостатки:
- 1. Несовершенство метода. Приближенный метод не гарантирует получение точного значения синуса, возможны погрешности и отклонения от точного результата.
- 2. Ограничения в точности. Приближенный метод может быть менее точным, чем точный метод, особенно при работе с углами близкими к 90 градусам или 270 градусам.
- 3. Зависимость от выбранного метода. Качество приближенного метода может зависеть от выбора конкретного алгоритма или формулы, что может ограничить область его применения.
Таким образом, применение приближенного метода для нахождения градусной меры синуса имеет свои преимущества, такие как простота и доступность, а также недостатки, включающие несовершенство метода и ограничения в точности. При выборе метода важно учитывать конкретные требования и ограничения задачи, а также наличие точных альтернативных методов, которые могут обеспечить более высокую точность результатов.
Преимущества использования приближенного метода

Одним из главных преимуществ приближенного метода является его простота и удобство в использовании. Даже без использования сложных формул и математических операций можно получить достаточно точное значение градусной меры синуса.
Приближенный метод также позволяет получать результаты с высокой степенью точности. Путем увеличения числа итераций можно добиться еще более точного результата. Это особенно важно при работе с задачами, требующими высокой точности вычислений.
Кроме того, приближенный метод позволяет сократить время вычислений. В отличие от других методов, которые требуют сложных и длительных операций, приближенный метод основан на простых вычислениях и последовательности итераций.
Еще одним преимуществом приближенного метода является возможность его применения при решении различных задач. Он может быть использован для нахождения приближенных значений синуса в широком спектре задач, связанных с наукой, инженерией и другими областями, где требуются точные вычисления.
Таким образом, использование приближенного метода позволяет получить точные результаты вычислений с минимальными затратами времени и усилий. Он является удобным и эффективным инструментом для нахождения градусной меры синуса и решения различных математических задач.