Синус угла - одно из основных понятий тригонометрии, которое часто используется при решении задач и расчетах. Но что делать, если у вас нет под рукой таблицы значений синуса? В этой статье мы рассмотрим несколько простых способов, которые помогут вам найти значение синуса угла без необходимости обращаться к таблицам или калькулятору.
Первый способ - использование геометрического представления синуса. Для этого необходимо нарисовать единичную окружность и провести луч, образующий нужный угол. Далее, изображая прямоугольный треугольник, можно легко определить значение синуса, как отношение противолежащего катета к гипотенузе треугольника.
Второй способ - использование треугольника со сторонами 3, 4 и 5. Известно, что для прямоугольного треугольника, где две стороны образуют прямой угол, отношение катетов равно значению синуса угла. Таким образом, треугольник со сторонами 3, 4 и 5 будет иметь синусом равным 3/5.
Как видите, существуют простые геометрические методы, которые позволяют найти синус угла без необходимости использования таблицы. Но помните, что эти методы применимы только для некоторых значений углов, и для более точных расчетов все же рекомендуется использовать таблицы или калькуляторы.
Как найти синус угла без таблицы
Однако не всегда у нас есть таблица синусов, чтобы узнать значение синуса угла. В этом случае нужно знать несколько простых способов расчета синуса без таблицы. Вот некоторые из них:
1. Если у вас есть значение угла в градусах, вы можете использовать тригонометрическую формулу sin(угол) = sin(угол в радианах).
2. Для нахождения синуса угла можно воспользоваться формулой половинного угла: sin(α/2) = √((1 - cosα)/2), где α – исходный угол.
3. Еще один способ – использовать формулу синуса суммы двух углов: sin(α + β) = sinα · cosβ + cosα · sinβ.
4. В случае, если известны значения косинуса и тангенса угла, можно использовать тождество тангенса и синуса: sinα = tgα / √(1 + tg²α) или sinα = √(1 - cos²α).
Это лишь некоторые из методов для вычисления синуса угла без таблицы. На практике часто используются специальные калькуляторы или программы для расчета тригонометрических функций. Также существуют таблицы и диаграммы, которые упрощают нахождение значений синуса угла. Но знание этих простых формул и методов может быть полезным, когда нужно быстро рассчитать синус на устном экзамене или в другой ситуации, где нет доступа к таблицам или калькуляторам.
Применение геометрических фигур

Например, при решении задачи на нахождение синуса угла можно использовать прямоугольный треугольник. Зная длины катетов, можно применить теорему Пифагора для нахождения длины гипотенузы, а затем использовать соотношение между сторонами треугольника: синус угла равен отношению противолежащего катета к гипотенузе.
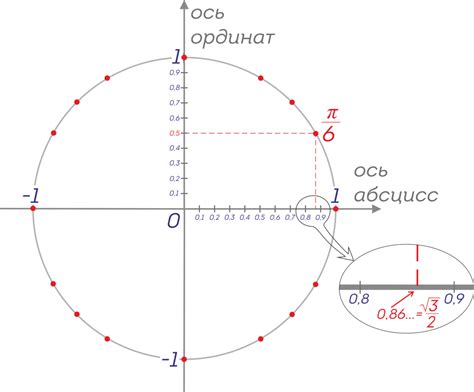
Также можно использовать тригонометрический круг, который является графическим представлением основных тригонометрических функций. На круге соединяют точку на окружности с началом координат и находят значение синуса по вертикальной координате этой точки. Этот метод особенно удобен при работе с углами, измеряемыми в радианах.
Также существуют специальные формулы и тригонометрические идентичности, которые позволяют находить синусы и другие тригонометрические функции при определенных условиях. Например, формулы синуса суммы и разности углов, формулы двойного и половинного угла, формула синуса тройного угла и так далее.
| Геометрическая фигура | Применение |
|---|---|
| Прямоугольный треугольник | Расчет синуса угла по длинам катетов и гипотенузы |
| Тригонометрический круг | Графическое представление синуса угла по его вертикальной координате на круге |
| Тригонометрические формулы и идентичности | Нахождение синусов углов при определенных условиях |
Таким образом, применение геометрических фигур является важным инструментом для нахождения синуса угла без использования таблицы. Оно позволяет визуализировать углы и представить их соотношения с помощью графических представлений или использовать специальные формулы и идентичности для расчетов.
Применение формулы синуса

Формула синуса имеет вид: sin(A) = a / c, где A - угол, a - длина противолежащей стороны, c - гипотенуза.
Чтобы найти синус угла с помощью этой формулы, необходимо знать длины сторон треугольника. Если длины сторон известны, можно подставить их значения в формулу и вычислить значение синуса угла.
Пример: пусть у нас есть треугольник со сторонами a = 6 и c = 10, и мы хотим найти синус угла A. Подставив значения в формулу, мы получим: sin(A) = 6 / 10 = 0.6. Таким образом, синус угла A равен 0.6.
Формула синуса можно применять в различных областях, включая геометрию, физику, инженерные и научные расчеты. Например, она часто используется для определения углов в треугольниках, а также для решения задач, связанных с телом, движущимся по криволинейной траектории.
Зная формулу синуса и имея необходимые данные, мы можем легко вычислить значение синуса угла без таблицы значений и использования специальных приборов.