Ортогональность векторов является важным концептом в линейной алгебре. Она означает, что два вектора перпендикулярны друг другу и составляют прямой угол. В нашем подробном руководстве мы расскажем о различных методах проверки ортогональности векторов.
Первый метод основан на определении скалярного произведения векторов. Для двух векторов A и B, если их скалярное произведение равно нулю, то они ортогональны. Примените формулу скалярного произведения для векторов и проверьте полученный результат.
Второй метод использует понятие ортогональной проекции вектора. Если проекция одного вектора на другой равна нулю, то они ортогональны. Расчет проекции вектора может быть выполнен с использованием специальной формулы, которую мы также рассмотрим в этом руководстве.
Наконец, рассмотрим геометрический подход. Векторы являются ортогональными, если они перпендикулярны на плоскости или в трехмерном пространстве. Проверьте, перпендикулярны ли ваши векторы с помощью графических методов, таких как построение векторов на координатной плоскости или использование трехмерных моделей в программном обеспечении.
Определение ортогональности векторов
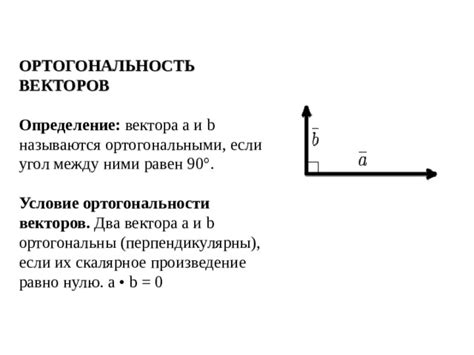
Для проверки ортогональности двух векторов, необходимо вычислить их скалярное произведение. Скалярное произведение двух векторов расчитывается по формуле:
a · b = a1 * b1 + a2 * b2 + ... + an * bn
Если скалярное произведение равно нулю, то векторы являются ортогональными. Если скалярное произведение не равно нулю, то векторы не являются ортогональными.
Также можно проверить ортогональность векторов, используя геометрический метод. Если два вектора перпендикулярны между собой, то их концы лежат на прямой, перпендикулярной этим векторам.
Зная координаты векторов, можно построить их на плоскости и провести перпендикулярную линию. Если векторы ортогональны, то перпендикулярная линия будет проходить через начало координат.
Значение ортогональности векторов в линейной алгебре

В линейной алгебре ортогональность векторов может быть проверена с помощью скалярного произведения, которое определяет угол их между собой. Если скалярное произведение равно нулю, то векторы являются ортогональными. Это можно записать формулой:
a · b = 0
где a и b - два вектора. Если данное уравнение выполняется, то можно сказать, что векторы a и b ортогональны друг другу. Если же скалярное произведение не равно нулю, то векторы не являются ортогональными.
Проверка ортогональности векторов представляет значительный интерес для решения различных задач в линейной алгебре. Например, ортогональные векторы могут быть использованы в качестве базиса для описания пространства, что облегчает вычисления и решение систем уравнений. Кроме того, ортогональность векторов играет важную роль в построении ортогональных проекций, ортогональных матриц и ортогональной декомпозиции векторов. Все эти концепции и методы находят широкое применение в различных областях науки, техники и приложений.
Как проверить ортогональность векторов в трехмерном пространстве

Для проверки ортогональности векторов в трехмерном пространстве следует выполнить следующие шаги:
- Запишите векторы в трехмерном виде. Например, вектор A может быть представлен как A = (a1, a2, a3), а вектор B как B = (b1, b2, b3).
- Вычислите скалярное произведение векторов A и B по формуле: AB = a1*b1 + a2*b2 + a3*b3.
- Если полученное значение скалярного произведения AB равно нулю, то векторы A и B являются ортогональными. Если значение не равно нулю, то векторы не являются ортогональными.
Для наглядности проверки ортогональности векторов в трехмерном пространстве можно использовать таблицу. В первом столбце таблицы указываются координаты вектора A, во втором столбце – координаты вектора B, а в третьем столбце – результат умножения соответствующих координат и сумма всех произведений.
| Вектор A | Вектор B | AB = a1*b1 + a2*b2 + a3*b3 |
|---|---|---|
| (a1, a2, a3) | (b1, b2, b3) | a1*b1 + a2*b2 + a3*b3 |
Если значение в третьем столбце равно нулю, то векторы A и B ортогональны. В противном случае, они не являются ортогональными.
Таким образом, следуя указанным шагам и использованию таблицы, можно легко проверить ортогональность векторов в трехмерном пространстве.
Как проверить ортогональность векторов в двумерном пространстве
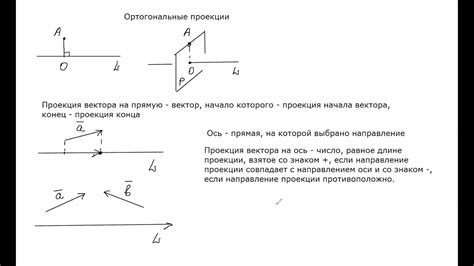
Определение: Векторы в двумерном пространстве называются ортогональными, если их скалярное произведение равно нулю.
Скалярное произведение векторов:
Для двух векторов а = (а₁, а₂) и б = (b₁, b₂) скалярное произведение определяется следующим образом:
a·b = а₁ * b₁ + а₂ * b₂
Шаги для проверки ортогональности:
- Задайте векторы, представленные в виде их координат (а₁, а₂) и (b₁, b₂).
- Вычислите скалярное произведение векторов по формуле a·b = а₁ * b₁ + а₂ * b₂.
- Если полученное значение скалярного произведения равно нулю, то векторы являются ортогональными. Если значение отличается от нуля, то векторы не являются ортогональными.
Пример:
Даны векторы а = (3, 4) и б = (5, -2).
Вычисляем скалярное произведение: a·b = 3 * 5 + 4 * (-2) = 15 - 8 = 7.
Полученное значение скалярного произведения не равно нулю, следовательно, векторы а и б не являются ортогональными.
Теорема ортогональности векторов и ее применение
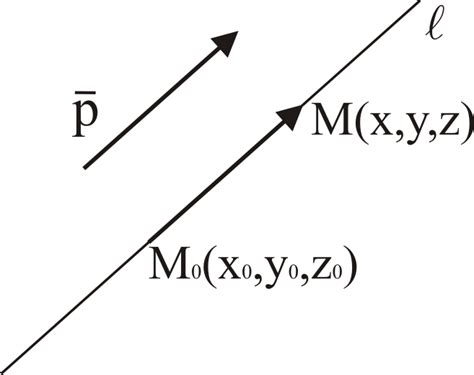
Теорема утверждает, что два вектора являются ортогональными, если и только если их скалярное произведение равно нулю. Скалярное произведение двух векторов определяется как сумма произведений соответствующих координат этих векторов. Если результат скалярного произведения равен нулю, то векторы ортогональны.
Ортогональность векторов имеет множество применений. Она может быть использована для проверки перпендикулярности линий и плоскостей в геометрии. В физике ортогональные вектора используются для описания направлений сил и моментов кручения. В компьютерной графике ортогональность векторов часто используется для расчета освещения и визуализации трехмерных объектов.
Ортогональность векторов также применяется в теории управления. Например, ортогональные базисные векторы могут быть использованы для упрощения сложных систем уравнений, таких как уравнения, описывающие движение объекта в пространстве.
При работе с векторами важно учитывать их ортогональность, так как она позволяет упростить множество вычислений и аналитических задач. Теорема ортогональности векторов служит основой для множества других математических концепций и применений, поэтому важно иметь хорошее понимание этой теоремы и уметь применять ее в различных сферах деятельности.
Способы проверки ортогональности векторов
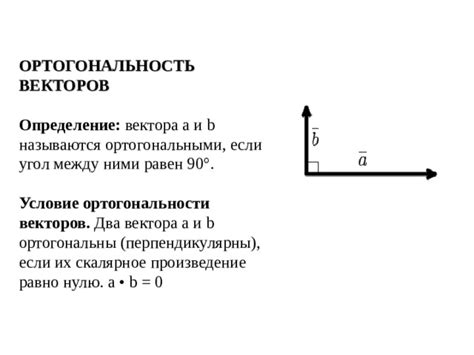
Существует несколько способов проверки ортогональности векторов. Рассмотрим два из них:
| Способ | Описание |
|---|---|
| 1. Проверка скалярного произведения | Для проверки ортогональности двух векторов a и b необходимо вычислить их скалярное произведение. Если результат равен нулю, то векторы ортогональны. |
| 2. Проверка угла между векторами | Другой способ проверки ортогональности векторов - это вычисление угла между ними. Если угол равен 90 градусов или пи/2 радиан, то векторы являются ортогональными. |
Разные способы проверки ортогональности векторов имеют свои преимущества и могут быть применены в различных ситуациях. Рекомендуется использовать тот способ, который наиболее удобен и подходит для конкретной задачи.
Примеры проверки ортогональности векторов
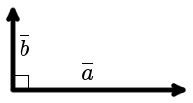
При проверке ортогональности векторов необходимо убедиться, что их скалярное произведение равно нулю. Ниже приведены несколько примеров, чтобы проиллюстрировать этот процесс.
Пример 1:
Даны два вектора: a = (2, 3, 1) и b = (-1, 2, 4).
Для проверки ортогональности векторов нужно вычислить их скалярное произведение:
(2 * -1) + (3 * 2) + (1 * 4) = -2 + 6 + 4 = 8.
Так как скалярное произведение не равно нулю, эти векторы не являются ортогональными.
Пример 2:
Даны два вектора: c = (-3, 1, 5) и d = (4, 2, -1).
Вычисляем их скалярное произведение:
(-3 * 4) + (1 * 2) + (5 * -1) = -12 + 2 - 5 = -15.
Так как скалярное произведение не равно нулю, эти векторы также не являются ортогональными.
Пример 3:
Даны два вектора: e = (0, 1, -2) и f = (3, 2, 1).
Скалярное произведение равно:
(0 * 3) + (1 * 2) + (-2 * 1) = 0 + 2 - 2 = 0.
Векторы e и f оказываются ортогональными, так как их скалярное произведение равно нулю.
Таким образом, проверка ортогональности векторов осуществляется путем вычисления их скалярного произведения и сравнения его с нулем. Если скалярное произведение равно нулю, векторы являются ортогональными, в противном случае - нет.
Расчет скалярного произведения векторов для проверки ортогональности

Скалярное произведение двух векторов вычисляется с использованием формулы:
Где A и B - это два вектора с координатами A = (A1, A2, A3) и B = (B1, B2, B3), а точка "·" обозначает скалярное произведение.
Для проверки ортогональности векторов необходимо вычислить скалярное произведение и проверить, равно ли оно нулю. Если скалярное произведение равно нулю, то векторы ортогональны. Если же скалярное произведение не равно нулю, то векторы не являются ортогональными.
Расчет скалярного произведения векторов обычно является простой математической операцией. Для каждой пары соответствующих координат векторов необходимо умножить их значения и сложить полученные произведения. Затем сумма всех произведений дает значение скалярного произведения.
Например, для векторов A = (2, 3, -1) и B = (-1, 4, 5) можно вычислить скалярное произведение следующим образом:
A · B = (2 * -1) + (3 * 4) + (-1 * 5)
A · B = -2 + 12 - 5 = 5
Таким образом, скалярное произведение данных векторов равно 5. Поскольку оно не равно нулю, можно заключить, что векторы A и B не являются ортогональными.
Таким образом, вычисление скалярного произведения векторов помогает проверить их ортогональность. Этот метод является надежным способом определить, являются ли два вектора ортогональными или нет.
Критерий ортогональности векторов и его использование
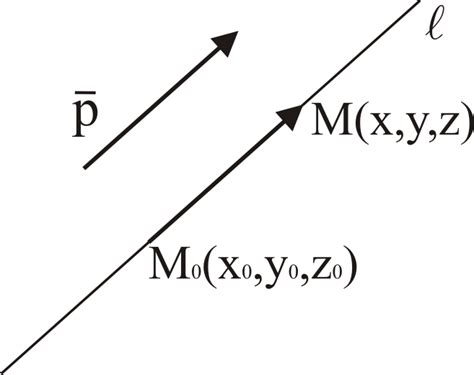
Для проверки ортогональности двух векторов A и B мы можем использовать следующий критерий:
- Вычислим скалярное произведение векторов A и B. Для двух трехмерных векторов A = (x1, y1, z1) и B = (x2, y2, z2), скалярное произведение может быть вычислено следующим образом: A·B = x1*x2 + y1*y2 + z1*z2.
- Если скалярное произведение равно нулю, то векторы A и B ортогональны. То есть, A и B перпендикулярны друг другу.
- Если скалярное произведение не равно нулю, то векторы A и B не являются ортогональными.
Применение критерия ортогональности векторов может быть полезным во многих задачах. Например, в геометрии, критерий ортогональности может быть использован для определения, являются ли два линейных отрезка перпендикулярными друг другу. В физике критерий ортогональности может быть использован, например, для определения момента силы относительно опорной точки. В компьютерной графике критерий ортогональности может быть использован для оптимизации расчетов или обработки изображений.
