Геометрия – это наука, изучающая пространственные отношения и формы. Все мы знакомы с классической евклидовой геометрией, которую изучаем в школе. Но что вы знаете о неевклидовой геометрии? Она описывает другие математические модели пространства, отличные от привычных нам законов.
В отличие от евклидовой геометрии, где применяются пять постулатов, неевклидова геометрия основана на непротиворечивой математической системе, в которой один или несколько постулатов евклидовой геометрии не выполняются или заменяются другими. Разбиение неевклидовой геометрии на две разных модели – геометрию Лобачевского и геометрию Римана – позволяет рассмотреть два взаимно противоречивых способа изучения пространства.
Неевклидова геометрия имеет ряд практических применений в различных областях науки и техники. Она находит свое применение в теории относительности, астрономии, физике, космологии и других дисциплинах. Благодаря неевклидовой геометрии ученые могут изучать законы и явления, которые не поддается объяснению в рамках евклидовой геометрии.
Определение неевклидовой геометрии

В отличие от классической геометрии Евклида, в которой справедливы аксиомы параллельности (либо аксиома о параллельных прямых, либо аксиома о третьем угле), неевклидовая геометрия исследует геометрические системы, в которых справедливость этих аксиом оказывается нарушенной.
Существует два основных типа неевклидовой геометрии:
- Геометрия Лобачевского - изучает геометрические системы с отрицательной кривизной, в которых выполняется аксиома о параллельных прямых.
- Геометрия Римана - изучает геометрические системы с положительной кривизной, в которых нарушается аксиома о параллельных прямых. В геометрии Римана кривизна может быть пространственной (геометрия трехмерного пространства) или геометрической (геометрия поверхностей).
Неевклидова геометрия имеет широкое применение в различных областях науки и техники, таких как общая теория относительности, космология, криптография и компьютерная графика. Изучение неевклидовой геометрии позволяет получить новые интуитивные представления о пространстве и расширяет возможности анализа и моделирования сложных физических и геометрических систем.
Принципы неевклидовой геометрии
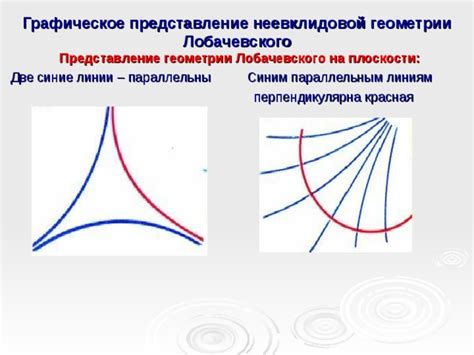
Неевклидова геометрия основана на принципах, которые отличаются от классической евклидовой геометрии. В евклидовой геометрии аксиомы описывают пространство, в котором мы живем, как плоское и бесконечное. Однако в неевклидовой геометрии, которая развилась в XIX веке, приняты другие аксиомы, основанные на работе немецкого математика Карла Гаусса и венгерского математика Яноша Боляя.
Основной принцип неевклидовой геометрии заключается в том, что наличие параллельных линий не является обязательным. В пространстве, описываемом неевклидовой геометрией, возможны различные типы параллельных линий и углов, которые не соответствуют аксиомам классической геометрии Евклида. Это приводит к возникновению новых геометрических законов и свойств, которые отличаются от тех, которые были лежат в основе евклидовой геометрии на протяжении многих столетий.
Неевклидова геометрия имеет большое практическое применение в различных областях науки и искусства. Она используется в физике, космологии, компьютерной графике, архитектуре и дизайне. Например, в теории относительности Альберта Эйнштейна используется идея неевклидовой геометрии для описания кривизны пространства и времени. В компьютерной графике неевклидова геометрия позволяет создавать трехмерные изображения с эффектами искажения перспективы. Также в архитектуре и дизайне неевклидовая геометрия используется для создания необычных форм и пространств, которые отличаются от обычных евклидовых конструкций.
Применение неевклидовой геометрии

Неевклидова геометрия, в отличие от евклидовой геометрии, позволяет рассматривать пространства с необычными геометрическими свойствами. Применение неевклидовой геометрии находит свое применение в различных областях:
1. Гравитационная физика:
Неевклидова геометрия играет важную роль в теории относительности Альберта Эйнштейна. Она описывает гравитацию как кривизну пространства и времени, что дает новое понимание взаимодействия масс и энергии.
2. Космология:
Неевклидовая геометрия используется в космологии для изучения структуры Вселенной и ее развития. Она позволяет моделировать пространство в соответствии с космологическими моделями и предсказывать различные космические явления.
3. Инженерия и строительство:
Неевклидова геометрия может быть использована в инженерных расчетах и строительстве, особенно при проектировании объектов с необычной формой или в нестандартных условиях. Она позволяет учесть особенности пространства и применить соответствующие геометрические принципы.
4. Криптография:
Одно из применений неевклидовой геометрии в криптографии - это использование эллиптических кривых для шифрования данных. Такие кривые обладают особыми алгебраическими свойствами и обеспечивают высокий уровень безопасности в сравнении с классическими алгоритмами.
5. Моделирование сложных систем:
Неевклидовая геометрия может быть использована для моделирования сложных систем, таких как социальные сети, сети передачи данных и физические сети. Она позволяет учесть нелинейные взаимодействия и распределения в пространстве, что помогает более точно предсказывать их поведение.
Все эти применения неевклидовой геометрии свидетельствуют о ее важности и актуальности в различных областях науки и техники.