Длина дуги и площадь сектора - важные параметры в геометрии, которые часто встречаются при решении различных задач. Знание соответствующих формул позволяет точно определить эти значения и использовать их в различных практических ситуациях.
Длина дуги представляет собой длину части окружности, ограниченной двумя заданными точками. Для ее вычисления используется формула:
L = 2πrα/360°
где L - длина дуги, r - радиус окружности, а α - центральный угол, измеряемый в градусах.
Площадь сектора представляет собой площадь части круга, образованного центральным углом и дугой, ограниченной двумя заданными точками. Формула для вычисления площади сектора имеет вид:
S = πr²α/360°
где S - площадь сектора, r - радиус окружности, а α - центральный угол, измеряемый в градусах.
Данные формулы позволяют с легкостью определить длину дуги и площадь сектора в различных задачах. Применимость этих формул подтверждают такие примеры, как вычисление длины окружности пути движения частицы или площади сектора в задаче о торте. Знание основных формул геометрии - важный инструмент в решении разнообразных задач, и формулы для вычисления длины дуги и площади сектора являются неотъемлемой частью этого инструментария.
Как найти длину дуги и площадь сектора

Когда речь заходит о геометрии, нахождение длины дуги и площади сектора может показаться сложной задачей. Однако, с помощью определенных формул и примеров расчетов, можно легко найти эти значения. В этом разделе мы рассмотрим, как найти длину дуги и площадь сектора.
Длина дуги - это сумма всех отрезков, составляющих дугу, а площадь сектора - это площадь фигуры, ограниченной двумя радиусами и дугой. Найдем формулы для этих значений:
Формула для нахождения длины дуги:
L = (r * θ) / 360, где L - длина дуги, r - радиус окружности, а θ - центральный угол в градусах.
Для расчета площади сектора используется следующая формула:
S = (π * r^2 * θ) / 360, где S - площадь сектора, π - число Пи (приблизительно 3.14), r - радиус окружности, а θ - центральный угол в градусах.
Теперь рассмотрим примеры использования этих формул.
Пример 1:
Допустим, у нас есть окружность с радиусом 10 см и центральным углом 60 градусов. Чтобы найти длину дуги, мы используем формулу L = (r * θ) / 360:
L = (10 * 60) / 360 = 6.66 см
Пример 2:
Предположим, у нас есть окружность с радиусом 8 см и центральным углом 120 градусов. Чтобы найти площадь сектора, мы используем формулу S = (π * r^2 * θ) / 360:
S = (3.14 * 8^2 * 120) / 360 = 67.20 см^2
Теперь вы знаете, как найти длину дуги и площадь сектора окружности с помощью соответствующих формул. Помните, что эти значения могут быть полезными при решении различных геометрических задач.
Формулы для расчета длины дуги
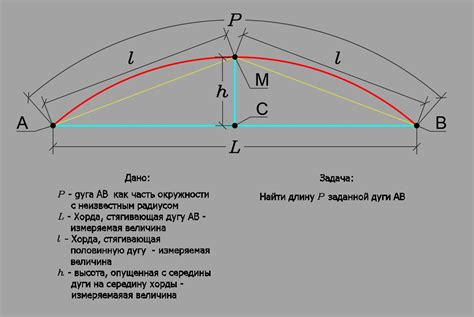
1. Длина дуги окружности:
Длина дуги (L) = радиус (r) × центральный угол (α) (в радианах)
2. Длина дуги сектора:
Для вычисления длины дуги сектора необходимо знать радиус окружности (r) и центральный угол сектора (α). Формула для расчета длины дуги сектора:
Длина дуги сектора (L) = (2πr × α) / 360°
3. Длина дуги эллипса:
Формула для расчета длины дуги эллипса выглядит следующим образом:
Длина дуги эллипса (L) = π × (а + b) × (1 + (3h / (10 + √(4 - 3h))))
Где:
а и b – большая и малая полуоси эллипса;
h – разность между большей и малой полуосью эллипса.
Теперь вы знаете основные формулы для расчета длины дуги окружности, сектора и эллипса. Используйте их в своих расчетах и задачах, чтобы получать точные и надежные результаты!
Примеры расчета длины дуги
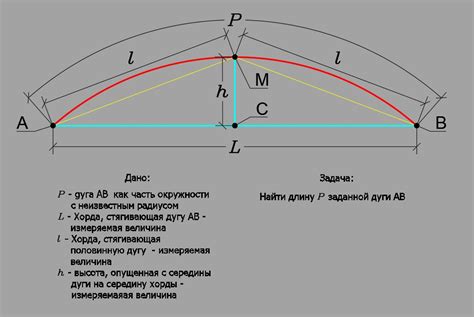
Рассмотрим несколько примеров расчета длины дуги.
| Пример | Значение угла α (в градусах) | Значение радиуса r (в единицах) | Длина дуги L |
|---|---|---|---|
| Пример 1 | 60° | 5 | 5π |
| Пример 2 | 90° | 8 | 4π |
| Пример 3 | 120° | 10 | 10π/3 |
Для расчета длины дуги необходимо знать значение угла α и радиуса r. Формула для расчета длины дуги задана следующим образом:
L = απr/180
Где L - длина дуги, α - значение угла в градусах, π - математическая константа (приблизительно равна 3,14159), r - радиус.
В примере 1, при угле α равном 60° и радиусе r равном 5, длина дуги составит 5π.
В примере 2, при угле α равном 90° и радиусе r равном 8, длина дуги составит 4π.
В примере 3, при угле α равном 120° и радиусе r равном 10, длина дуги составит 10π/3.
Таким образом, расчет длины дуги является простым применением формулы и позволяет получить точное значение этой величины.
Формулы для расчета площади сектора
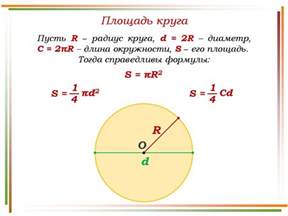
1. Если известен радиус круга (r) и величина центрального угла (α), тогда площадь сектора (S) можно вычислить по формуле:
S = (π * r^2 * α) / 360
2. Если известен длина дуги (l) и радиус круга (r), то площадь сектора (S) можно найти по формуле:
S = (π * r * l) / (2 * π * r) = l / 2
3. Если известена площадь сектора (S) и радиус круга (r), то можно найти величину центрального угла (α) по следующей формуле:
α = (S * 360) / (π * r^2)
Пользуясь этими формулами, можно легко расчитать площадь сектора, зная нужные параметры..
Примеры расчета площади сектора

Пусть у нас имеется сектор с центральным углом α и радиусом r. Для расчета площади сектора можно использовать формулу:
S = (π * r^2 * α) / 360,
где S - площадь сектора, π - число пи (приближенное значение 3.14159), r - радиус сектора, α - центральный угол сектора.
Например, пусть дан сектор с радиусом 5 метров и центральным углом 60 градусов. Чтобы найти площадь этого сектора, используем формулу:
S = (3.14159 * 5^2 * 60) / 360 = 26.17993 м2.
Таким образом, площадь данного сектора составляет приблизительно 26.17993 м2.
Знание формулы для расчета площади сектора позволяет эффективно решать задачи связанные с геометрическими фигурами и использовать их в практических примерах.
Важные соображения при расчете длины дуги и площади сектора

При расчете длины дуги и площади сектора важно учитывать несколько факторов. Эти важные соображения помогут правильно выполнить расчеты и получить точные значения.
1. Знание формул. Для расчета длины дуги и площади сектора необходимо знать соответствующие математические формулы. Формула для расчета длины дуги зависит от радиуса и угла сектора, а формула для расчета площади сектора зависит от радиуса и угла сектора.
2. Измерения. Важно правильно измерить радиус и угол сектора. Для измерения радиуса можно использовать линейку или специальные инструменты, например, компас. Угол сектора можно измерить с помощью транспортира или специальных геометрических инструментов.
3. Перевод единиц измерения. При расчете длины дуги и площади сектора необходимо учитывать единицы измерения, в которых даны исходные данные. Если радиус дан в сантиметрах, а требуется получить ответ в метрах, необходимо выполнить соответствующий перевод.
4. Точность расчетов. Важно учесть точность измерений и округление значений. Если измерения не точны или округление произведено неправильно, это может привести к неточным результатам при расчете длины дуги и площади сектора.
5. Понимание применимости. Важно понимать, в каких случаях можно применять формулы для расчета длины дуги и площади сектора. Например, данные формулы применяются для расчета длины дуги и площади сектора на плоскости или в трехмерном пространстве, но не применяются для расчета длины дуги или площади сектора на поверхности сферы.
Использование указанных важных соображений при расчете длины дуги и площади сектора поможет получить точные значения и избежать ошибок при выполнении этих расчетов.