Пирамида - величественная и загадочная форма геометрических фигур, которая вдохновляет и привлекает внимание многих математиков и любителей геометрии. В своей сущности пирамида представляет собой многогранник, у которого одна из граней называется основанием, а все остальные грани являются треугольниками, сходящимися в вершину пирамиды.
Объем пирамиды – это одна из ее основных характеристик, которая определяет, сколько пространства занимает данная фигура. Обычно для расчета объема пирамиды требуется знать ее высоту. Однако, что делать, если высота пирамиды неизвестна? В таких случаях существуют специальные формулы и методы, позволяющие найти объем пирамиды без высоты.
Одной из таких формул является формула площади основания пирамиды. Если известна площадь основания, то по этой формуле можно вычислить объем пирамиды. Другой способ – это использование соотношения площади основания и объема пирамиды с помощью формулы пирамиды. В обоих случаях не требуется знание высоты пирамиды.
Расчет объема пирамиды
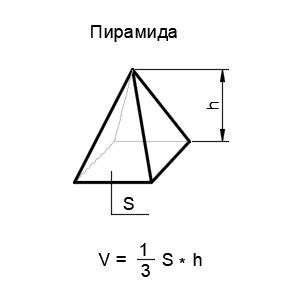
- Определите форму пирамиды. В зависимости от формы будут использоваться разные формулы для расчета объема. Например, для правильной пирамиды используется формула V = (S * h) / 3, где V – объем пирамиды, S – площадь основания пирамиды, h – высота пирамиды.
- Если у вас нет данных о высоте пирамиды, но есть информация о площади основания и боковых гранях, можно использовать формулу V = (l1 * l2 * l3) / (6 * h), где V – объем пирамиды, l1, l2, l3 – длины боковых граней пирамиды, h – высота пирамиды. Эта формула работает для правильной пирамиды с треугольной основой.
- Если вы не знаете ни высоту пирамиды, ни площадь основания, но есть данные о диагоналях равностороннего треугольника, можно воспользоваться формулой V = (d1 * d2 * d3) / (12 * h), где V – объем пирамиды, d1, d2, d3 – диагонали треугольника, h – высота пирамиды.
Используя соответствующую формулу, вы сможете легко рассчитать объем пирамиды, даже если у вас нет данных о высоте. Учтите только, что все значения должны быть выражены в одной системе измерения – в метрах, сантиметрах или других.
Формула для нахождения объема пирамиды без высоты
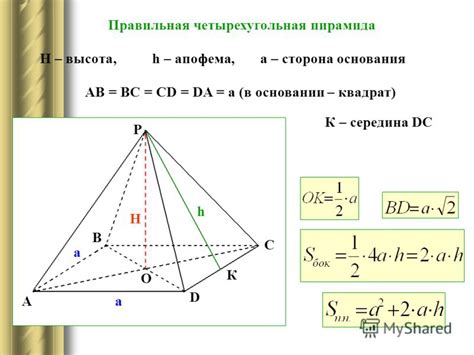
Оказывается, существует специальная формула, которая позволяет нам найти объем пирамиды без высоты. Для этого нам необходимо знать площадь основания пирамиды и некоторую вспомогательную величину, называемую высотой пирамиды из верхней точки основания.
Формула для нахождения объема пирамиды без высоты имеет вид:
Объем = (1/3) * Площадь основания * Высота пирамиды из верхней точки основания
Теперь разберемся, как получить значение высоты пирамиды из верхней точки основания. Для этого воспользуемся теоремой Пифагора. Если мы знаем длины ребра пирамиды и длину диагонали основания, то можем найти высоту.
Итак, формула для нахождения высоты пирамиды выглядит следующим образом:
Высота = √(Диагональ² - (Ребро/2)²)
Теперь, когда у нас есть формула для нахождения объема пирамиды без высоты, мы можем легко решать задачи, связанные с данным вопросом. Просто подставьте известные значения в формулы и получите результат.
Примеры расчетов объема пирамиды
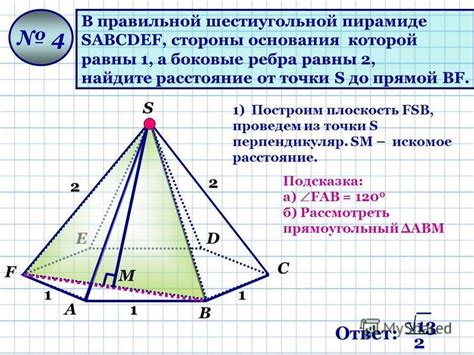
Для наглядности рассмотрим несколько примеров расчетов объема пирамиды.
Пример 1:
Известно, что площадь основания пирамиды равна 36 квадратных сантиметров, а высота равна 5 сантиметров. Найдем объем пирамиды.
Сначала найдем площадь основания пирамиды:
36 см²
Затем используем формулу для расчета объема пирамиды:
V = (1/3) * S * h
где V - объем пирамиды, S - площадь основания, h - высота пирамиды.
Подставляем значения в формулу:
V = (1/3) * 36 см² * 5 см
V = (1/3) * 180 см³
V = 60 см³
Таким образом, объем пирамиды равен 60 кубическим сантиметрам.
Пример 2:
Известно, что площадь основания пирамиды равна 25 квадратных метров, а высота равна 8 метров. Найдем объем пирамиды.
Сначала найдем площадь основания пирамиды:
25 м²
Затем используем формулу для расчета объема пирамиды:
V = (1/3) * S * h
где V - объем пирамиды, S - площадь основания, h - высота пирамиды.
Подставляем значения в формулу:
V = (1/3) * 25 м² * 8 м
V = (1/3) * 200 м³
V = 66.67 м³
Таким образом, объем пирамиды равен 66.67 кубическим метрам.
Пример 3:
Известно, что площадь основания пирамиды равна 64 квадратных дециметра, а высота равна 6 дециметров. Найдем объем пирамиды.
Сначала найдем площадь основания пирамиды:
64 дм²
Затем используем формулу для расчета объема пирамиды:
V = (1/3) * S * h
где V - объем пирамиды, S - площадь основания, h - высота пирамиды.
Подставляем значения в формулу:
V = (1/3) * 64 дм² * 6 дм
V = (1/3) * 384 дм³
V = 128 дм³
Таким образом, объем пирамиды равен 128 кубическим дециметрам.
Использование формулы для практических задач

Расчет объема пирамиды без известной высоты может быть полезен во множестве практических ситуаций. Например, если мы знаем массу подсолнечного масла, которое помещается в пирамидальную бутыль определенной формы, то можем использовать формулу для определения объема пирамиды и, соответственно, емкости бутыли.
Другой пример - определение объема затопленного пространства в бассейне, имеющего форму пирамиды, после сильного дождя. Зная площадь основания пирамиды и измеряя изменение уровня воды, мы можем использовать формулу для расчета объема затопленного пространства.
Еще одним практическим примером может быть архитектурное проектирование. Например, для определения объема наклонной пирамидальной крыши на здании, зная площадь основания и угол наклона.
Использование формулы для практических задач помогает нам определить объем пирамиды, не зная высоты, и применить это знание в различных сферах нашей жизни.
Пример расчета объема пирамиды при известной площади основания
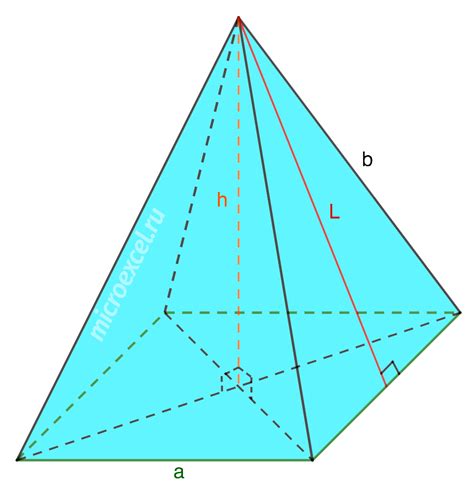
Допустим, у нас есть пирамида с площадью основания S = 36 квадратных сантиметров и высотой h = 10 сантиметров. Для нахождения объема пирамиды воспользуемся формулой:
V = (1/3) * S * h
Подставим значения в формулу:
V = (1/3) * 36 * 10 = (1/3) * 360 = 120
Таким образом, объем пирамиды составляет 120 кубических сантиметров.
Пример расчета объема пирамиды при известных длинах ребер
Рассмотрим пример расчета объема пирамиды, когда известны длины ее ребер.
Пусть у нас есть пирамида с четырьмя треугольными гранями, и известны длины ее ребер:
AB = 6 см, BC = 8 см, AC = 10 см.
Для расчета объема пирамиды сначала найдем площадь основания, используя формулу Герона:
S = √p(p - AB)(p - BC)(p - AC),
где p - полупериметр треугольника, который можно найти по формуле:
p = (AB + BC + AC) / 2.
В нашем случае, p = (6 + 8 + 10) / 2 = 12 см.
Теперь найдем площадь основания:
S = √12(12 - 6)(12 - 8)(12 - 10) = √12 * 6 * 4 * 2 = 24 см².
Затем, нам необходимо найти высоту пирамиды, которую можно найти с использованием формулы:
h = V / S,
где V - объем пирамиды, S - площадь основания.
Для нашего случая, площадь основания равна 24 см².
Предположим, что мы знаем, что пирамида равносторонняя, поэтому высота пирамиды будет перпендикулярна основанию и попадает в его центр. Таким образом, h будет равно отрезку, проведенному из вершины пирамиды до его центра основания, обозначенному точкой O.
Очевидно, что треугольки AOB, BOC и COA будут равнобедренными с основаниями AB, BC и AC соответственно, поскольку центр O является центром основания пирамиды и также будет равноудален от вершин.
Тогда, мы можем получить длину высоты пирамиды AO с использованием теоремы Пифагора в треугольнике прямоугольном OAB:
AO² = AB² - BO²,
где BO - половина одной из сторон основания пирамиды.
Поскольку пирамида равносторонняя, то BO = AB / 2, следовательно:
AO² = AB² - (AB / 2)² = AB² - AB² / 4 = 3 / 4 * AB².
Таким образом, AO = √(3 * AB² / 4).
Теперь, мы можем найти высоту пирамиды h, используя найденные значения:
h = √(3 * AB² / 4) = √(3 * 6² / 4) = √54 ≈ 7.35 см.
Наконец, вычислим объем пирамиды при известной высоте:
V = (S * h) / 3 = (24 * 7.35) / 3 ≈ 56 см³.
Таким образом, объем пирамиды с ребрами длиной AB = 6 см, BC = 8 см и AC = 10 см равен примерно 56 см³.