Диагональ параллелепипеда - это линия, соединяющая две противоположные вершины этой фигуры. Как найти диагональ параллелепипеда по его сторонам? Это вопрос, с которым могут столкнуться люди, занимающиеся геометрией или строительством. На самом деле, расчет диагонали параллелепипеда довольно прост. Для этого необходимо знать значение трех его сторон.
Параллелепипед - это геометрическая фигура, у которой все грани являются прямоугольниками. Он имеет шесть граней, восемь вершин и двенадцать ребер. Ширина, высота и глубина параллелепипеда - это три его стороны. Для расчета диагонали параллелепипеда можно использовать теорему Пифагора.
Теорема Пифагора гласит, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Применительно к параллелепипеду, где диагональ является гипотенузой, стороны - катетами, мы можем использовать эту теорему для нахождения длины диагонали. Формула выглядит следующим образом: квадрат диагонали параллелепипеда равен сумме квадратов его сторон.
Что такое диагональ параллелепипеда?
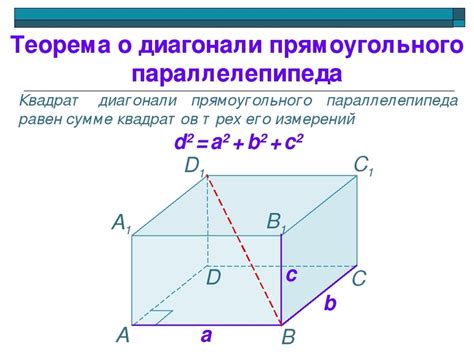
Диагональ параллелепипеда является важной характеристикой этой геометрической фигуры, поскольку предоставляет информацию о ее размерах и форме. Для нахождения длины диагонали параллелепипеда необходимо знать длины всех его сторон или размеры его ребер.
Знание длины диагонали параллелепипеда может быть полезно при решении различных задач и проблем, связанных с геометрией, инженерией и архитектурой. Оно позволяет определить, например, могут ли объекты проходить через проемы с заданными размерами, или насколько он будет удобен для использования в конкретных условиях.
Начальные данные
Решение и формула

Для нахождения диагонали параллелепипеда по его сторонам применяется формула:
Диагональ = √(a² + b² + c²),
где a, b и c - стороны параллелепипеда.
Для примера, предположим, что у нас есть параллелепипед со сторонами:
- a = 5 см,
- b = 8 см,
- c = 10 см.
Подставим значения в формулу:
Диагональ = √(5² + 8² + 10²) = √(25 + 64 + 100) = √(189) ≈ 13.75 см.
Таким образом, диагональ этого параллелепипеда составляет около 13.75 см.
Пример вычисления

Для вычисления диагонали параллелепипеда по его сторонам необходимо использовать теорему Пифагора.
Допустим, у нас есть параллелепипед с длинной стороны a, шириной стороны b и высотой стороны c.
Согласно теореме Пифагора, диагональ параллелепипеда d можно найти с помощью следующей формулы:
d = √(a² + b² + c²)
Давайте рассмотрим пример:
У нас есть параллелепипед с длиной стороны a = 4, шириной стороны b = 3 и высотой стороны c = 5.
Подставляем значения в формулу:
d = √(4² + 3² + 5²) = √(16 + 9 + 25) = √50 ≈ 7.07
Таким образом, диагональ параллелепипеда будет примерно равна 7.07.