Длина дуги окружности - одна из основных характеристик, связанных с геометрией окружности. Она представляет собой расстояние между двумя точками на окружности, измеренное по самой окружности. Расчет длины дуги окружности может быть полезен в различных сферах, таких как архитектура, строительство и инженерия.
Формула для расчета длины дуги окружности выглядит следующим образом: L = 2πr(α/360), где L - длина дуги, r - радиус окружности, α - центральный угол, измеренный в градусах. Данная формула основывается на связи между длиной дуги и центральным углом, который соответствует этой дуге.
Давайте рассмотрим пример расчета длины дуги окружности. Предположим, у нас есть окружность с радиусом 10 см и центральным углом 60°. Воспользуемся формулой L = 2πr(α/360), подставляя значения в соответствующие переменные: L = 2π * 10 * (60/360) = 10π см. Таким образом, длина дуги окружности составляет 10π см.
Теперь вы знаете, как найти длину дуги окружности, используя соответствующую формулу. Это может быть полезным инструментом для решения различных задач, связанных с геометрией окружности. Не забывайте использовать правильные единицы измерения и округлять результаты по необходимости.
Формула для расчета длины дуги окружности

Формула для расчета длины дуги окружности имеет следующий вид:
L = 2πr(α/360),
где L - длина дуги окружности,
π - математическая константа, приблизительно равная 3.14159,
r - радиус окружности,
α - центральный угол в градусах, между двумя направленными отрезками, определяющими дугу.
Для использования этой формулы необходимо знать значения радиуса и центрального угла окружности. Зная эти значения, можно легко вычислить длину дуги окружности.
Давайте рассмотрим пример расчета длины дуги окружности. Пусть задана окружность с радиусом r = 5 и центральным углом α = 60°. Для вычисления длины дуги окружности воспользуемся приведенной формулой:
L = 2π * 5 * (60/360) = 5π/3 ≈ 5.24.
Таким образом, длина дуги окружности составляет примерно 5.24 единицы длины.
Формула для расчета длины дуги окружности позволяет легко вычислять эту величину при заданных параметрах радиуса и центрального угла. Она находит применение в различных областях, таких как геометрия, физика, а также в промышленности и строительстве.
Как найти радиус окружности, если известна длина дуги

Если известна длина дуги окружности, то можно рассчитать радиус, используя следующую формулу:
| Формула: | Радиус = Длина дуги / Угловое расстояние |
|---|
Длина дуги измеряется в единицах длины, таких как метры или сантиметры, а угловое расстояние измеряется в радианах. Если угол задан в градусах, его следует перевести в радианы, умножив на π/180.
Приведем пример расчета радиуса окружности, если известна длина дуги. Пусть длина дуги составляет 12 метров, а угловое расстояние равно π/4 радиан.
| Длина дуги (L) | 12 м |
|---|---|
| Угловое расстояние (θ) | π/4 рад |
Применим формулу для нахождения радиуса:
| Радиус (r) = | Длина дуги (L) / Угловое расстояние (θ) |
|---|---|
| 12 м / (π/4 рад) | |
| 12 м / (0.785 рад) | |
| 15.27 м |
Таким образом, радиус окружности равен 15.27 м.
Теперь вы знаете, как найти радиус окружности, если известна длина дуги, используя соответствующую формулу и простое вычисление.
Расчет длины дуги окружности по углу сектора

Расчет длины дуги окружности по углу сектора осуществляется по следующей формуле:
| Формула | Обозначение |
|---|---|
| L = 2πR(α/360°) | где L - длина дуги окружности, R - радиус окружности, α - угол сектора в градусах |
Таким образом, для расчета длины дуги окружности необходимо знать радиус окружности и угол сектора в градусах. Зная эти параметры, можно легко определить длину дуги окружности по указанной формуле.
Рассмотрим пример расчета длины дуги окружности по углу сектора:
Пусть радиус окружности R = 5 см, а угол сектора α равен 60°.
Используя формулу L = 2πR(α/360°), подставим известные значения:
L = 2π * 5 * (60/360) = 2π * 5 * 0.1667 ≈ 5π ≈ 15.71 см
Таким образом, длина дуги окружности по углу сектора, при данных значениях, составляет примерно 15.71 см.
Важно помнить, что значения радиуса и угла сектора должны быть выражены в одной системе измерения (например, сантиметры и градусы), чтобы получить правильный результат.
Как найти длину дуги окружности в градусах и радианах
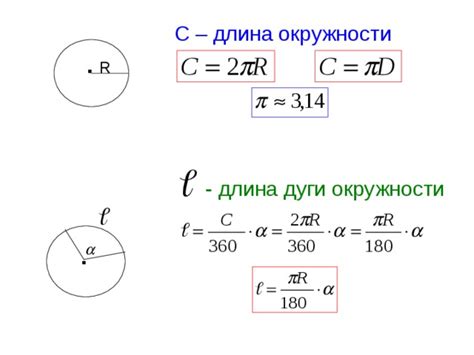
Чтобы найти длину дуги окружности в градусах, воспользуйтесь формулой:
Длина дуги (в градусах) = (длина окружности * угол) / 360
Например, для окружности радиусом 5 см и угла дуги в 60 градусов:
- Найдем длину окружности: длина окружности = 2 * π * радиус = 2 * 3.14 * 5 = 31.4 см
- Подставим значения в формулу: длина дуги (в градусах) = (31.4 * 60) / 360 = 5.23 см
Чтобы найти длину дуги окружности в радианах, воспользуйтесь следующей формулой:
Длина дуги (в радианах) = радиус * угол
Пример: для окружности радиусом 7 см и угла дуги в 1.5 радиана:
- Подставим значения в формулу: длина дуги (в радианах) = 7 * 1.5 = 10.5 см
Теперь вы знаете, как находить длину дуги окружности как в градусах, так и в радианах.
Примеры расчета длины дуги окружности
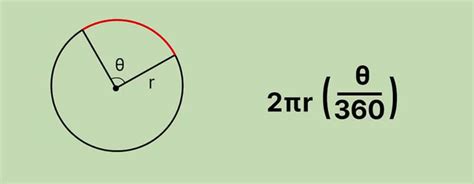
Длина дуги окружности может быть вычислена, зная ее радиус и центральный угол. Рассмотрим несколько примеров расчета длины дуги окружности.
Пример 1:
Дано: радиус окружности R = 5 см, центральный угол α = 30°.
Длина дуги окружности вычисляется по формуле: L = 2πR(α/360°).
Подставляем известные значения: L = 2π(5 см)(30°/360°).
Рассчитываем: L = 2π(5 см)(0.0833).
Получаем результат: L ≈ 3.49 см.
Пример 2:
Дано: радиус окружности R = 10 м, центральный угол α = 90°.
Длина дуги окружности вычисляется по формуле: L = 2πR(α/360°).
Подставляем известные значения: L = 2π(10 м)(90°/360°).
Рассчитываем: L = 2π(10 м)(0.25).
Получаем результат: L ≈ 15.71 м.
Пример 3:
Дано: радиус окружности R = 8 дм, центральный угол α = 180°.
Длина дуги окружности вычисляется по формуле: L = 2πR(α/360°).
Подставляем известные значения: L = 2π(8 дм)(180°/360°).
Рассчитываем: L = 2π(8 дм)(0.5).
Получаем результат: L ≈ 25.13 дм.