Длина окружности – это одна из важнейших характеристик, определяющих геометрические свойства окружности. Она показывает, насколько длинный отрезок нужно пройти, чтобы обойти всю окружность. Расчет длины окружности между двумя точками может быть важным действием в различных ситуациях, от геодезии до программирования. В этой статье мы рассмотрим пошаговую инструкцию, как вычислить длину окружности между двумя заданными точками.
Шаг 1: Определите координаты точек. Для расчета длины окружности нам необходимо знать координаты двух точек. Обозначим эти точки как A(x1, y1) и B(x2, y2), где x1, y1, x2 и y2 – числа, представляющие значения координат этих точек.
Шаг 2: Вычислите расстояние между точками. Используя формулу расстояния между двумя точками на плоскости, найдите расстояние между точками A и B:
AB = √((x2 - x1)^2 + (y2 - y1)^2)
где √ обозначает операцию извлечения квадратного корня, (x2 - x1)^2 означает квадрат разности между x2 и x1, а (y2 - y1)^2 – квадрат разности между y2 и y1.
Шаг 3: Вычислите длину окружности. Для вычисления длины окружности используйте формулу:
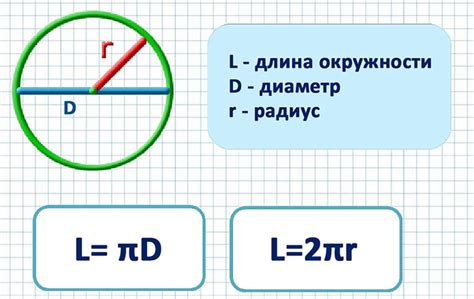
Длина окружности = 2πr
где r - радиус окружности.
Шаг 4: Найдите радиус окружности. Радиус окружности можно найти, используя расстояние между двумя точками:
r = AB/2
где AB – расстояние между двумя точками.
Шаг 5: Подставьте значения в формулу. Подставьте найденное значение радиуса в формулу для длины окружности и вычислите ее:
Длина окружности = 2πr
Теперь вы знаете, как пошагово вычислить длину окружности между двумя заданными точками. Следуя этой инструкции, вы сможете проделать этот расчет в любом контексте, где он может оказаться полезным.
Расчет длины окружности между двумя точками: пошаговая инструкция
Если у вас есть две точки на плоскости и вы хотите найти длину окружности между ними, следуйте этой пошаговой инструкции:
Шаг 1: Определите координаты двух точек.
Измерьте или найдите значения x и y для каждой точки. Обозначим координаты первой точки как (x1, y1) и второй точки как (x2, y2).
Шаг 2: Вычислите разницу между координатами точек по оси x и по оси y.
Вычтите координаты x1 и x2, чтобы получить разницу по оси x: Δx = x2 - x1.
Вычтите координаты y1 и y2, чтобы получить разницу по оси y: Δy = y2 - y1.
Шаг 3: Возведите разности координат в квадрат.
Умножьте Δx на Δx и Δy на Δy: Δx² = Δx * Δx, Δy² = Δy * Δy.
Шаг 4: Сложите квадраты разностей координат.
Сложите Δx² и Δy²: Δx² + Δy² = сумма квадратов разностей координат.
Шаг 5: Извлеките квадратный корень из суммы квадратов разностей координат.
Извлеките корень квадратный из суммы Δx² и Δy²: √(Δx² + Δy²) = расстояние между двумя точками.
Шаг 6: Умножьте полученное расстояние на 2π, чтобы найти длину окружности.
Умножьте полученное расстояние на 2π: длина_окружности = 2π * расстояние.
Примечание: Если вам известен радиус окружности, вы можете использовать формулу длины окружности C = 2πr, где C - длина окружности, π - математическая константа π (пи), и r - радиус окружности. Однако, если вам даны только координаты двух точек, вы должны использовать вышеуказанный метод для расчета длины окружности.
Шаг 1: Изучение определения окружности
Для полного понимания расчета длины окружности между двумя точками необходимо знать следующие основные понятия, связанные с окружностью:
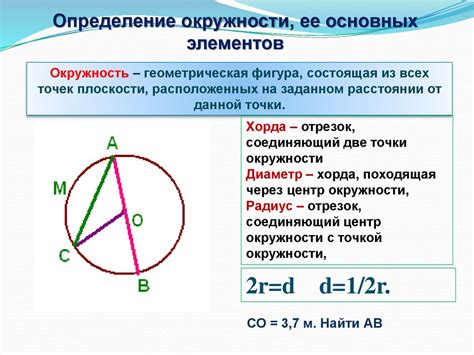
| Термин | Описание |
| Центр окружности | Точка, расположенная в середине окружности. Обозначается буквой "O". |
| Радиус окружности | Расстояние от центра окружности до любой ее точки. Обозначается буквой "r". |
| Диаметр окружности | Отрезок, соединяющий две точки на окружности и проходящий через ее центр. Обозначается буквой "d". Диаметр равен удвоенному значению радиуса (d = 2r). |
| Длина окружности | Общая длина кривой линии окружности. Обозначается буквой "C". |
На данном этапе важно полностью усвоить эти основные понятия, так как они будут использоваться при расчете длины окружности между двумя точками.
Шаг 2: Определение координат точек
Чтобы определить координаты точек, можно использовать различные способы:
| Способ | Описание | Пример |
|---|---|---|
| Использование координатной плоскости | Можно использовать координатную плоскость, где ось x соответствует горизонтальному положению точки, а ось y - вертикальному. | (3, 4) |
| Использование географических координат | Если точки находятся на земной поверхности, то их координаты можно определить с использованием географической широты и долготы. | (55.75, 37.62) |
| Использование других систем координат | В некоторых случаях может потребоваться использовать другую систему координат, например, полярные координаты. | (r, θ) |
После определения координат точек, можно приступить к следующему шагу - расчету длины окружности.
Шаг 3: Применение формулы расчета расстояния между точками

Теперь, когда мы определили координаты обеих точек, мы можем приступить к применению формулы для расчета расстояния между ними.
Формула для расчета расстояния между двумя точками на плоскости имеет следующий вид:
| Формула | Расчет |
|---|---|
| d = √((x2 - x1)2 + (y2 - y1)2) | где d - расстояние между точками (x1, y1) - координаты первой точки |
Мы подставляем значения координат в формулу и выполняем необходимые математические операции. Результатом будет получение расстояния между двумя точками на плоскости.
Давайте рассмотрим пример:
У нас есть 2 точки: A(3, 4) и B(7, 9). Применим формулу для расчета расстояния между ними:
d = √((7 - 3)2 + (9 - 4)2)
d = √(42 + 52)
d = √(16 + 25)
d = √41
Таким образом, расстояние между точками A(3, 4) и B(7, 9) равно √41 единиц.
Теперь, когда мы понимаем, как применять формулу для расчета расстояния между точками, мы можем перейти к следующему шагу - расчету длины окружности между двумя заданными точками.
Шаг 4: Умножение расстояния на коэффициент для получения окружности

Для расчета длины окружности между двумя точками необходимо умножить расстояние между ними на коэффициент.
Коэффициент вычисляется по формуле: π / 180, где π (пи) равно приблизительно 3.14159 и 180 является числом градусов в полном круге.
Умножение расстояния между двумя точками на коэффициент позволит перевести угловое расстояние в линейное расстояние, что является длиной окружности.
Пример:
Предположим, что расстояние между двумя точками составляет 10 градусов. Мы умножаем это значение на коэффициент (π / 180) и получаем примерно 0.1745.
Итак, длина окружности между этими двумя точками составляет примерно 0.1745 единиц (например, сантиметры или метры), в зависимости от выбранной системы измерения расстояния.