Цилиндр - это геометрическое тело, которое состоит из двух параллельных круговых оснований и боковой поверхности, которая соединяет эти основания. Расчет различных параметров цилиндра может понадобиться в разных сферах, от инженерии до математики. В данной статье мы расскажем, как найти длину окружности основания цилиндра и предоставим подробное руководство по этому вопросу.
Для того чтобы найти длину окружности основания цилиндра, нам необходимо знать радиус или диаметр окружности. Если у вас есть радиус, то формула расчета длины окружности выглядит следующим образом:
Длина окружности = 2πr
Где π (пи) - это математическая константа, примерное значение которой равно 3,14.
Если у вас есть диаметр, а не радиус, то вместо радиуса следует использовать половину диаметра (диаметр / 2) в формуле расчета длины окружности основания цилиндра.
Теперь, когда вы знаете формулу, вы можете легко найти длину окружности основания цилиндра, используя известные вам данные. Эта информация может быть полезна для решения различных задач, связанных с цилиндрами, таких как расчет объема или поверхности цилиндра.
Запомните, что правильные расчеты и формулы являются основой для точности в решении задач. Удачи в изучении геометрии и математики!
Определение длины окружности

Длина окружности = 2πr
где π - математическая константа, приближенное значение которой равно 3.14159, а r - радиус окружности.
Для расчета длины окружности необходимо знать ее радиус. Радиус - это расстояние от центра окружности до любой точки на ней. Если радиус уже известен, то просто умножьте его на 2π, чтобы получить длину окружности.
Зная длину окружности основания цилиндра, вы можете использовать эту информацию для решения различных задач, связанных с цилиндрическими формами, таких как вычисление объема или площади поверхности цилиндра.
Определение основы цилиндра
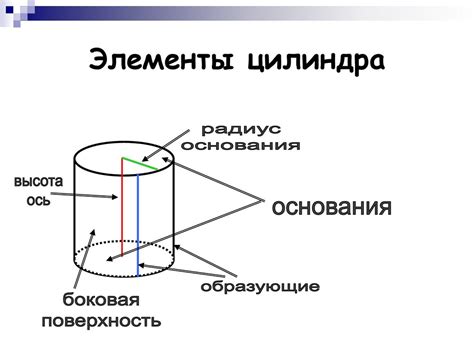
Круглый цилиндр имеет две окружности в качестве основы, которые параллельны друг другу и находятся на противоположных концах цилиндра. Радиус окружности основы обозначается как r, а диаметр - 2r.
Если окружность основы цилиндра задана радиусом r, то длина его окружности (C) может быть вычислена по формуле:
C = 2πr
Где π (пи) - это математическая константа, приближенное значение которой равно 3,14159.
Зная длину окружности основы цилиндра, вы можете проводить различные расчеты и измерения, связанные с цилиндром, такие как его объем и площадь поверхности.
Значение PI и его использование
Значение ПИ широко используется в геометрии и физике для расчета различных параметров окружности, сферы и эллипса. Оно играет важную роль в науке и технике, а также в различных областях, связанных с математикой.
Для расчета длины окружности основания цилиндра используется формула: длина окружности = 2πr, где "r" - радиус окружности. Подставляя значение ПИ (π) в эту формулу, мы можем получить точное значение длины окружности.
Значение ПИ также используется в других формулах и уравнениях, связанных с геометрией, тригонометрией и анализом. Благодаря своей универсальности и точности, число ПИ является одной из самых важных математических констант.
Формула расчета длины окружности
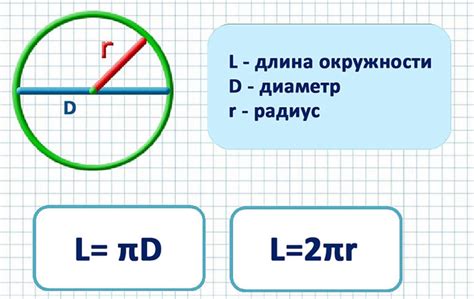
Для расчета длины окружности основания цилиндра используется простая математическая формула:
C = 2πr,
где C - длина окружности, π - математическая константа π (пи), приблизительное значение которой равно 3.14159, а r - радиус окружности основания цилиндра.
Таким образом, для определения длины окружности основания цилиндра необходимо знать значение радиуса и использовать данную формулу.
Пример:
Допустим, что радиус основания цилиндра составляет 3 см. Тогда, для расчета длины окружности применяем формулу:
C = 2π × 3 см.
Значение π примерно равно 3.14159, поэтому окончательный расчет будет следующим:
C ≈ 2 × 3.14159 × 3 ≈ 18.84956 см.
Таким образом, длина окружности основания данного цилиндра составляет примерно 18.85 см.
Примеры вычисления длины окружности
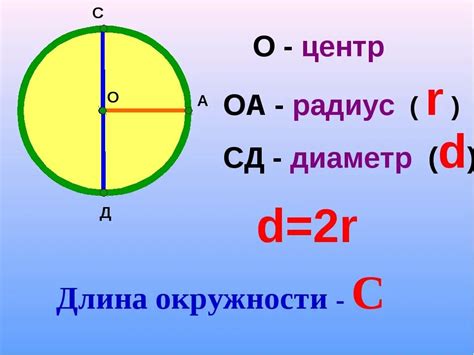
Давайте рассмотрим несколько примеров для вычисления длины окружности основания цилиндра:
Пример 1:
Пусть радиус окружности основания цилиндра равен 5 сантиметров. Чтобы найти длину окружности, воспользуемся формулой C = 2πr, где С обозначает длину окружности, а r - радиус. Подставив значения в формулу, получим C = 2 * 3.14 * 5 = 31.4 сантиметра. Таким образом, длина окружности основания цилиндра равна 31.4 сантиметра.
Пример 2:
Пусть дано значение диаметра, равное 10 метров. Чтобы найти длину окружности, нужно сначала найти радиус - половину диаметра. В данном случае, радиус будет равен 5 метров. Затем воспользуемся формулой C = 2πr и подставим значения: C = 2 * 3.14 * 5 = 31.4 метра. Таким образом, длина окружности основания цилиндра равна 31.4 метра.
Это лишь несколько примеров применения формулы для расчета длины окружности основания цилиндра. В зависимости от данного значения - радиуса или диаметра - можно легко вычислить длину окружности.
Рекомендации по проверке результатов
После вычисления длины окружности основания цилиндра, рекомендуется провести проверку результатов, чтобы убедиться в их точности. Вот несколько советов, которые помогут вам выполнить эту задачу:
- Проверьте используемую формулу. Убедитесь, что вы правильно применили формулу для расчета длины окружности. Проверьте значения радиуса и пи. Если найдены ошибки в формуле, исправьте их и пересчитайте результат.
- Сравните результат с другими методами. Если у вас есть возможность, выполните расчет длины окружности основания цилиндра с использованием другого метода или программы. Сравните полученные результаты и убедитесь, что они совпадают. Если результаты отличаются, перепроверьте свои вычисления и устраните возможные ошибки.
- Округление и точность. Учтите, что округление чисел может влиять на конечный результат. Обратите внимание на количество знаков после запятой в полученном значении и убедитесь, что оно соответствует требованиям задачи. Если требуется большая точность, проверьте, корректно ли выполняется округление в вашей программе или калькуляторе.
- Проверка визуально. Визуальная проверка может помочь в обнаружении видимых ошибок. Найдите изображение цилиндра с указанием его размеров и сравните его с вашим результатом. Убедитесь, что ваша вычисленная длина окружности основания соответствует ожидаемому значению.
- Повторное вычисление. Если после всех проверок вы все еще сомневаетесь в результате, выполните расчет еще раз. Возможно, вы упустили что-то или допустили небольшую ошибку. При повторном вычислении обычно проявляются возможные ошибки и их можно исправить.
Следуя этим рекомендациям, вы сможете проверить результаты расчета длины окружности основания цилиндра и быть уверенными в их точности. Отдельное внимание уделите правильности использования формулы и правильности округления чисел, чтобы исключить возможные ошибки.