Треугольник - одна из основных геометрических фигур, которая имеет огромное значение в различных научных и практических областях. Базовые понятия, такие как стороны треугольника и его углы, играют важную роль во многих вычислениях. Косинус треугольника - это одна из основных тригонометрических функций, которая позволяет рассчитывать значения углов треугольника.
Формула косинуса для треугольника выражает отношение длины стороны треугольника к прилежащему ей углу. Эта формула может быть использована для вычисления любого угла треугольника, если известны длины сторон. Зная длины сторон треугольника a, b и c, а также угол α между сторонами a и b, можно рассчитать косинус угла α по следующей формуле:
cos(α) = (b² + c² - a²) / (2bc)
Различные практические ситуации требуют использования косинуса треугольника. Например, при расчете расстояния между двумя точками на плоскости можно использовать теорему косинусов для вычисления длины прямой. Также косинус треугольника находит применение в задачах определения высоты объектов, рассчете силы тяжести, определения площади треугольника и т. д.
Давай рассмотрим пример расчета косинуса треугольника. Пусть дан треугольник ABC, в котором известна длина стороны AB, равная 5, длина стороны BC, равная 7, и угол BAC, равный 60 градусам. Используя формулу косинуса, мы можем рассчитать косинус угла BAC:
cos(60) = (7² + 5² - 7 * 5 * cos(60)) / (2 * 7 * 5)
Как рассчитать косинус треугольника с помощью формулы
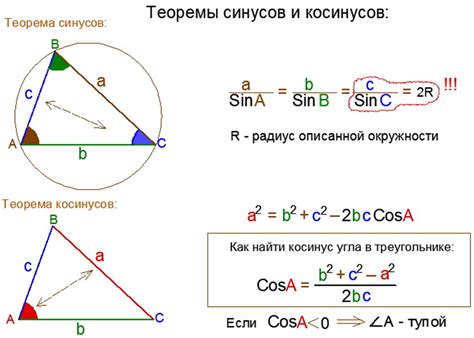
cos(α) = a / c
где α – угол между гипотенузой и прилегающим катетом, а и с – длины соответствующих сторон треугольника.
Например, пусть у нас есть треугольник ABC, в котором известны длины катетов AB = 3 и BC = 4. Чтобы найти косинус угла α, нужно подставить значения в формулу:
cos(α) = 3 / 5
cos(α) = 0.6
Таким образом, косинус угла α равен 0.6.
Формула расчета косинуса
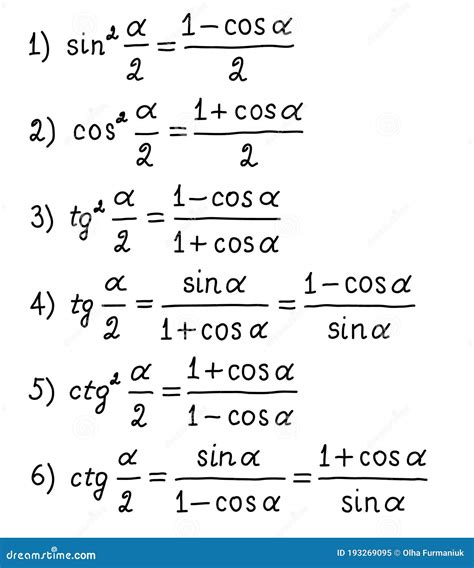
- Для расчета косинуса острого угла α:
cos(α) = adjacent / hypotenuse
- где adjacent - длина прилегающего катета,
- hypotenuse - длина гипотенузы.
Зная значения данных сторон треугольника, можно легко вычислить косинус заданного угла.
Например, если треугольник имеет прилегающий катет длиной 4 единицы и гипотенузу длиной 5 единиц, то для расчета косинуса угла α:
cos(α) = 4 / 5 = 0.8
Таким образом, косинус угла α равен 0.8.
Примеры расчетов косинуса треугольника
Для наглядности рассмотрим несколько примеров расчета косинуса треугольника.
Пример 1:
Пусть у нас имеется прямоугольный треугольник ABC, где угол A равен 90 градусов, длина катета AB равна 3, а гипотенуза AC равна 5. Найдем косинус угла B.
- Найдем длину другого катета BC, используя теорему Пифагора: BC = sqrt(AC^2 - AB^2) = sqrt(5^2 - 3^2) = 4.
- Применяя определение косинуса треугольника, получаем: cos(B) = AB/AC = 3/5 = 0.6.
Пример 2:
Рассмотрим произвольный треугольник XYZ, где сторона XY равна 6, сторона YZ равна 8, а сторона XZ равна 10. Найдем косинус угла Y.
- Применяя формулу косинуса треугольника, получаем: cos(Y) = (XY^2 + YZ^2 - XZ^2) / (2 * XY * YZ) = (6^2 + 8^2 - 10^2) / (2 * 6 * 8) = 44/96 ≈ 0.4583.
Пример 3:
Пусть дан треугольник PQR со сторонами PQ = 4, QR = 7 и PR = 9. Найдем косинус угла Q.
- Применяя формулу косинуса треугольника, получаем: cos(Q) = (PQ^2 + QR^2 - PR^2) / (2 * PQ * QR) = (4^2 + 7^2 - 9^2) / (2 * 4 * 7) = 16/56 ≈ 0.2857.
Это лишь некоторые примеры расчетов косинуса треугольника. Формула применима для треугольников любой формы и размеров.
Пример расчета косинуса по готовым значениям сторон
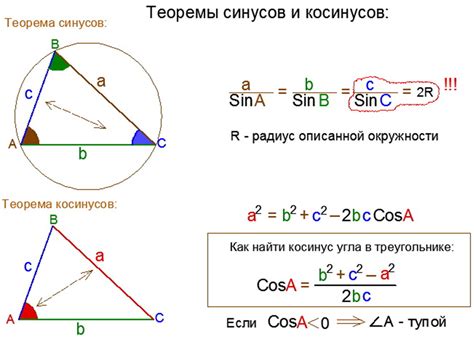
Рассмотрим конкретный пример расчета косинуса треугольника, если известны значения его сторон.
Допустим, у нас есть треугольник ABC, у которого известны значения сторон:
- AB = 5
- BC = 4
- AC = 3
Чтобы найти косинус угла A, мы можем воспользоваться формулой:
cos(A) = (BC2 + AC2 - AB2) / (2 * BC * AC)
Подставим значения сторон треугольника в формулу:
cos(A) = (42 + 32 - 52) / (2 * 4 * 3) = (16 + 9 - 25) / 24 = 0 / 24 = 0
Таким образом, косинус угла A в данном треугольнике равен 0.
Косинус треугольника очень полезен в геометрии и тригонометрии, так как позволяет находить значения углов, зная длины сторон треугольника, и наоборот.