Косинус треугольника - одна из основных геометрических величин, которая позволяет определить угол между двумя его сторонами. Для расчета косинуса треугольника необходимо знать длины всех его сторон и координаты вершин. Эта информация позволяет применить теорему косинусов и получить значение косинуса требуемого угла.
Для начала, найдем длины сторон треугольника по его координатам. Для этого воспользуемся формулой расстояния между двумя точками в декартовой системе координат:
AB = √((x2 - x1)2 + (y2 - y1)2)
После вычисления длин сторон треугольника, можно приступить к расчету косинуса:
cosα = (b2 + c2 - a2) / (2 * b * c)
Где α - угол между сторонами b и c, a - сторона, противолежащая углу α.
Теперь, зная значение косинуса треугольника, можно определить его угол при помощи функции обратного косинуса, известной как арккосинус (acos). Эта функция позволяет найти угол по его косинусу:
α = arccos(cosα)
Таким образом, зная координаты вершин треугольника, мы можем рассчитать его косинус и определить угол между двумя его сторонами.
Что такое косинус треугольника?
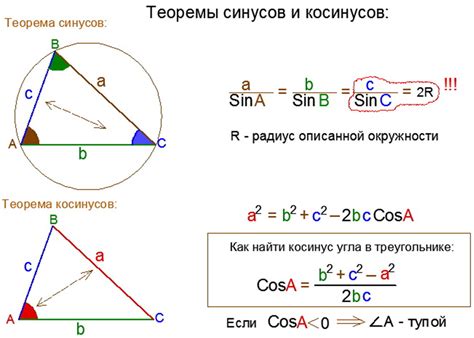
Косинус треугольника обозначается как cos, и его значение находится по формуле:
cos(α) = a / c,
где α - угол между сторонами треугольника, a - длина ближайшей к этому углу стороны треугольника, c - длина гипотенузы треугольника (стороны, противолежащей углу α).
Зная значения сторон треугольника и угла между ними, можно рассчитать косинус треугольника и использовать его в различных задачах. Косинус треугольника может быть использован для определения длины сторон треугольника по углам или нахождения углов треугольника по длинам его сторон.
Понятие косинуса треугольника
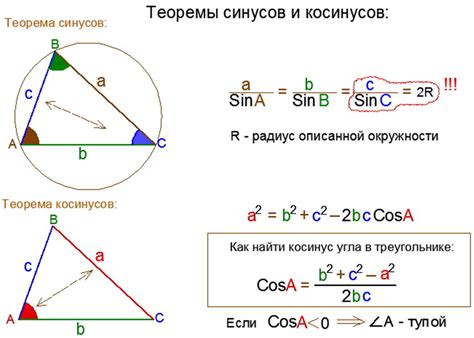
Косинус треугольника может быть вычислен по формуле:
cos(α) = adjacent / hypotenuse
Где:
- cos(α) - значение косинуса угла α
- adjacent - длина прилежащего катета (стороны) треугольника
- hypotenuse - длина гипотенузы (главной стороны) треугольника
Знание значения косинуса треугольника позволяет определить углы и длины сторон треугольника по заданным координатам его вершин.
Формула расчета косинуса треугольника
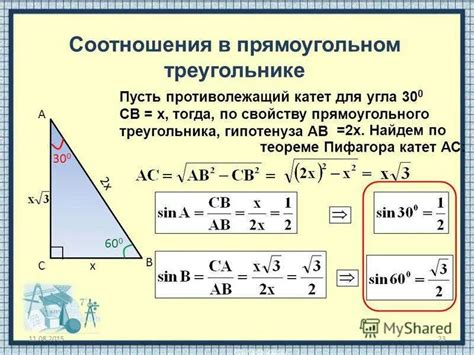
Для расчета косинуса треугольника по его координатам используется формула, основанная на теореме косинусов.
Теорема косинусов гласит, что в любом треугольнике квадрат длины одной из сторон равен сумме квадратов длин двух других сторон, умноженной на удвоенное произведение этих сторон на косинус угла между ними.
Для треугольника ABC с координатами вершин A(x1, y1), B(x2, y2) и C(x3, y3), расстояния между вершинами можно вычислить с помощью формулы расстояния между двумя точками:
d(A, B) = √((x2 - x1)^2 + (y2 - y1)^2)
d(B, C) = √((x3 - x2)^2 + (y3 - y2)^2)
d(C, A) = √((x1 - x3)^2 + (y1 - y3)^2)
Соответственно, для вычисления косинуса угла A треугольника ABC, основываясь на теореме косинусов, используется следующая формула:
cos(A) = (d(B, C)^2 + d(C, A)^2 - d(A, B)^2) / (2 * d(B, C) * d(C, A))
Вычисление косинуса треугольника по его координатам позволяет определить углы треугольника и провести его дальнейший анализ и обработку с использованием геометрических методов и принципов.
Как рассчитать косинус треугольника по формуле
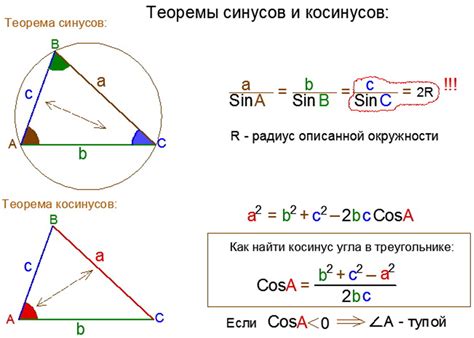
Косинус треугольника можно вычислить по формуле, используя длины его сторон и закон косинусов. Закон косинусов гласит:
Квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон, умноженной на двойной произведение этих сторон на косинус угла, образованного этими сторонами:
a2 = b2 + c2 - 2bc * cos(A)
b2 = a2 + c2 - 2ac * cos(B)
c2 = a2 + b2 - 2ab * cos(C)
где a, b и c - длины сторон треугольника, а A, B и C - соответствующие углы. Чтобы найти косинус одного из углов, необходимо переписать формулу, выражая косинус отдельного угла:
cos(A) = (b2 + c2 - a2) / (2bc)
cos(B) = (a2 + c2 - b2) / (2ac)
cos(C) = (a2 + b2 - c2) / (2ab)
Зная длины сторон треугольника, можно подставить их значения в формулы и вычислить косинусы углов.
Например, для треугольника со сторонами a = 3, b = 4 и c = 5, косинусы углов можно рассчитать следующим образом:
| Угол | Косинус |
|---|---|
| A | (42 + 52 - 32) / (2 * 4 * 5) |
| B | (32 + 52 - 42) / (2 * 3 * 5) |
| C | (32 + 42 - 52) / (2 * 3 * 4) |
Выполнив вычисления, получим:
| Угол | Косинус |
|---|---|
| A | 0.6 |
| B | -0.2 |
| C | 0.8 |
Таким образом, косинусы углов треугольника с сторонами a = 3, b = 4 и c = 5 равны: cos(A) = 0.6, cos(B) = -0.2 и cos(C) = 0.8.
Примеры вычисления косинуса треугольника
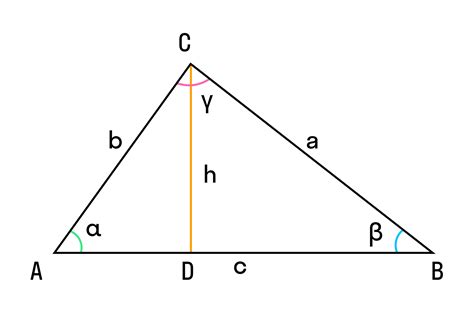
Ниже приведены примеры вычисления косинуса треугольника на основе заданных координат его вершин:
Пример 1:
Дан треугольник ABC с координатами вершин: A(0, 0), B(3, 0), C(3, 4). Для вычисления косинуса треугольника можно использовать формулу:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
где a, b, c - длины сторон треугольника, соответствующие углу A. В данном случае a = BC, b = AC и c = AB.
Подставляем известные значения в формулу:
cos(A) = (3^2 + 4^2 - 3^2) / (2 * 3 * 4) = 4 / 24 = 1 / 6 = 0.1667
Таким образом, косинус угла A треугольника ABC равен 0.1667.
Пример 2:
Дан треугольник XYZ с координатами вершин: X(2, 2), Y(6, 2), Z(4, 6). Также используем формулу:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c) для вычисления косинуса угла A треугольника XYZ.
Подставляем известные значения в формулу:
cos(A) = (4^2 + 4^2 - 2^2) / (2 * 4 * 4) = 32 / 64 = 0.5
Таким образом, косинус угла A треугольника XYZ равен 0.5.
Пример вычисления косинуса треугольника с заданными координатами
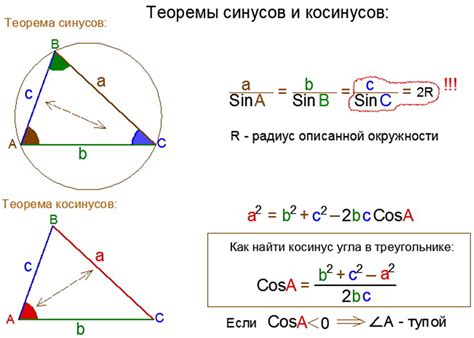
Для вычисления косинуса треугольника по заданным координатам его вершин, нам потребуется использовать формулу косинусов.
Пусть дан треугольник ABC, вершины которого имеют координаты (x1, y1), (x2, y2) и (x3, y3).
Сначала найдем длины сторон треугольника. Для этого нам понадобятся формулы расчета длины отрезка.
- Длина отрезка AB = √((x2 - x1)2 + (y2 - y1)2)
- Длина отрезка BC = √((x3 - x2)2 + (y3 - y2)2)
- Длина отрезка AC = √((x3 - x1)2 + (y3 - y1)2)
Затем вычислим косинус угла A треугольника ABC по формуле:
cos(A) = (AC2 + AB2 - BC2) / (2 * AC * AB)
Аналогично можно вычислить косинусы углов B и C треугольника ABC.
В результате получим значения косинусов трех углов треугольника.
В данной статье мы рассмотрели, как рассчитать косинус треугольника по его координатам. Косинус треугольника можно вычислить, используя формулу косинуса. Для этого необходимо знать значения длин сторон треугольника и угол между ними. Также мы изучили, какие функции необходимо использовать для вычисления косинуса и какие математические операции нужно выполнить.
Косинус треугольника является важным параметром при решении задач геометрии, физики и других наук. Он позволяет измерить отношение длин сторон треугольника к углу между ними и определить геометрические свойства треугольника.
Более детальное изучение вычисления косинуса треугольника и его применения может быть полезно для студентов, занимающихся геометрией и математикой, а также для профессионалов в области науки и инженерии. Надеемся, что данная статья помогла вам лучше понять, как вычислять косинус треугольника и применять его в практических задачах.
Удачи в дальнейших изысканиях!