Вы наверняка слышали о сферах и кубах, но знаете ли вы, как они взаимосвязаны? Вероятно, нет. Но не волнуйтесь, сегодня мы познакомим вас с удивительным отношением между этими двумя геометрическими фигурами.
Один из интересных фактов о кубе заключается в том, что его вписанная сфера – это сфера, которая идеально вписывается внутрь куба так, что ее центр совпадает с центром куба, а ее диаметр равен длине ребра куба.
Теперь вот что интересно: можем ли мы вычислить объем куба, зная радиус вписанной сферы? Ответ – да, мы можем!
Определение и свойства вписанной сферы в кубе
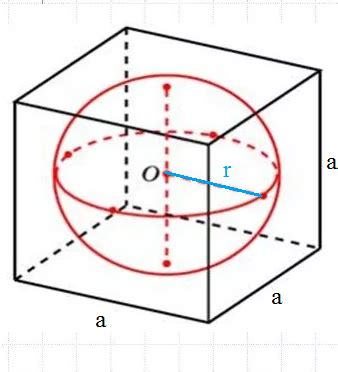
- Радиус вписанной сферы равен половине длины стороны куба. Это означает, что если известна длина стороны куба, радиус сферы можно найти, разделив длину стороны на 2.
- Диаметр вписанной сферы равен длине стороны куба. Диаметр сферы можно найти, умножив радиус на 2.
- Объем вписанной сферы можно вычислить, используя формулу 4/3πr³, где r - радиус вписанной сферы.
- Площадь поверхности вписанной сферы можно вычислить, используя формулу 4πr², где r - радиус вписанной сферы.
Вписанная сфера в кубе имеет ряд интересных свойств и может быть использована для решения различных геометрических задач. Знание её характеристик позволяет определить объем куба, а также провести другие вычисления и доказательства в геометрии.
Что такое вписанная сфера

Для куба с вписанной сферой, центр этой сферы совпадает с центром куба, а ее радиус равен половине длины ребра куба.
Вписанная сфера обладает некоторыми интересными свойствами. Например, диаметр вписанной сферы равен длине диагонали куба, а объем вписанной сферы может быть вычислен по формуле: V = (4/3)πr³, где V - объем сферы, π - математическая постоянная «пи», r - радиус вписанной сферы.
Использование вписанной сферы в рассчетах объема куба позволяет упростить задачу и ускорить вычисления.
Вписанная сфера является важным геометрическим понятием, используемым в различных областях науки и техники.
Свойства вписанной сферы в кубе
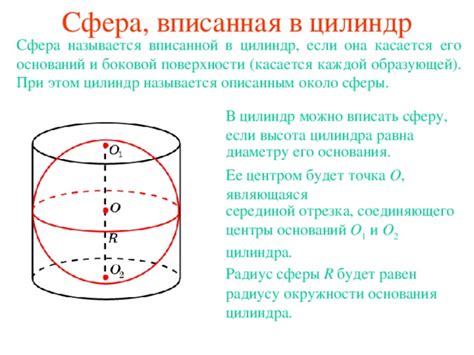
- 1. Сфера касается всех граней куба. Радиус вписанной сферы в кубе равен половине длины его диагонали.
- 2. Точка касания сферы с каждой гранью делит ее диагональ в отношение 1:2.
- 3. Диаметр вписанной сферы равен длине ребра куба.
- 4. Объем вписанной сферы в кубе можно найти по формуле: V = (4/3)πr³, где r – радиус вписанной сферы.
Свойства вписанной сферы в кубе играют важную роль при решении геометрических задач и имеют практическое применение. Например, в дизайне архитектурных объектов или создании упаковочного материала. Изучение этих свойств позволяет лучше понять взаимосвязь между сферой и кубом.
Формула для вычисления радиуса вписанной сферы через объем куба
Для нахождения радиуса вписанной сферы в кубе, необходимо использовать формулу, основанную на связи объема куба и радиуса внутренней сферы.
Пусть V обозначает объем куба, и R - радиус вписанной сферы. Используя геометрические соотношения между этими величинами, можно получить следующую формулу:
V = (4/3) * π * R^3
Для вычисления радиуса R из объема куба V необходимо привести уравнение к виду:
R^3 = (3 * V) / (4 * π)
Обе стороны уравнения возводятся в степень 1/3, после чего получаем окончательное выражение для радиуса:
R = ((3 * V) / (4 * π))^(1/3)
Итак, зная объем куба, можно найти радиус вписанной сферы через данную формулу.
Объем куба и радиус вписанной сферы
В данной теме мы рассмотрим, как найти объем куба, используя радиус вписанной сферы. Для этого мы воспользуемся формулой, которая связывает радиус сферы и объем куба.
Итак, пусть r - радиус вписанной сферы. Тогда диагональ куба (d) равна двух радиусов сферы (d = 2r). Зная диагональ куба, мы можем найти его ребро (a) по формуле a = d/√3.
Теперь, имея значение ребра куба (a), мы можем вычислить его объем (V) по формуле V = a^3.
Приведем подробные шаги для нахождения объема куба через радиус вписанной сферы:
- Найдите диагональ куба по формуле d = 2r, где r - радиус вписанной сферы.
- Вычислите ребро куба, используя формулу a = d/√3.
- Найдите объем куба, возведя значение ребра в куб: V = a^3.
Таким образом, зная радиус вписанной сферы, мы можем легко найти объем куба, используя описанный выше алгоритм. Это представляет практическую значимость при решении геометрических задач и в других областях, где требуется работа с кубическими формами.
Формула для вычисления радиуса вписанной сферы через объем куба

Радиус вписанной сферы может быть вычислен по формуле, используя объем куба и его свойства. Для этого необходимо знать, что вписанная сфера касается всех граней куба и плотно заполняет его объем.
Предположим, что сторона куба равна a, а его объем равен V. Тогда формула для нахождения радиуса вписанной сферы будет следующей:
| Формула | |
| Радиус вписанной сферы | = Радиус вписанной сферы = a/(2√3) |
Таким образом, радиус вписанной сферы может быть вычислен, если известны сторона куба и его объем. Используя эту формулу, можно определить радиус вписанной сферы, что может быть полезно во многих задачах геометрии и физики.